1. Introduction
Fe-6.5 wt.%Si is a kind of soft magnetic materials with high relative permeability, nearly zero magnetostriction, and low coercive force and low iron loss [1]. With its advantages of reducing the consumption of energy and noise pollution, Fe-6.5 wt.%Si can be widely used in transformers, motors, and electric relay [2,3]. However, the alloy is extremely hard to deform by the conventional rolling process, which seriously retards the development and industrial application of this alloy.
Structure ordering is inevitable for the Fe-6.5 wt.%Si alloy due to the high silicon content. According to the Fe-Si phase diagram, ordered structures like B2 (Pm3m) and DO3 (Fm3m) would form in the alloy [4,5]. Other ordered structures, such as Fe15Si and Fe7Si, can form in this alloy as well [[6], [7], [8]]. The ordered phases result in lattice resistance enhancement and anti-phase boundary formation, and hence hinder the cross slip of dislocations. Therefore, people consider that the embrittlement of the Fe-6.5 wt.%Si results from the structure ordering.
To avoid the brittleness at the room temperature, various techniques have been developed, including chemical vapor deposition (CVD) [9], spray forming [[10], [11], [12]], hot dipping [13], direct powder rolling (DPR) [14], etc. Hot-warm-cold rolling combined with proper heat treatments was reported to fabricate the sheets with thickness of 0.03-0.05 mm [[15], [16], [17]]. Especially, the rapid solidification technique attracted much attention owing to the short line fabrication and the good ductility of ribbons [[18], [19], [20]].
In comparison with the above techniques, the metallurgical routes using plastic deformation together with heat treatments are of great interests, because this processing can provide various possibilities to adjust the microstructures and properties of the products. For examples, good formability and surface quality can be achieved after cold rolling [21], and better magnetic performance can be obtained by texture control [22,23]. Shin et al. [24] investigated the cold workability of high silicon steels. The samples were hot rolled to 2 mm at 800-1200 °C, and after the heat treatment the samples were cold rolled repeatedly by continuously decreasing the roll gap to about 0.8 mm. Bi et al. [25,26] also investigated the ductility of this alloy. In their study, the sheet with a thickness of 0.35 mm was prepared by cold-rolling after hot-rolling.
The facts that the Fe-6.5 wt.%Si alloy with intrinsic embrittlement can be cold rolled proved that the formability can be improved by metallurgical approaches. The cold workability of the Fe-6.5 wt.%Si alloy can be much enhanced by reducing the ordering degree [[27], [28], [29]]. Thermo mechanical processes can decrease the ordering degree and soften the high silicon steel sheet [30]. The deformation-induced disordering and dynamic recovery are the reasons for the strain softening during warm deformation [[31], [32], [33]]. Our study suggested that the Fe-6.5 wt.%Si sheets with 0.05-0.30 mm thickness can be successfully fabricated through a metallurgical route [21].
Other methods, such as micro-alloying and changing the structural morphology, have been used to improve the ductility. Twinning deformation does not tend to occur in a metal with BCC crystal structures, owing to the high stacking fault energy. Yet, in recent years, twinning in the Fe-6.5 wt.%Si have been reported. Xie et al. [34] discovered that the columnar-grained Fe-6.5 wt.%Si alloy showed enhanced tensile ductility, which was resulted from the formation of homogeneous deformation twinning. Fu et al. [35] studied the effect of the grain orientation on twinning, and found that twinning was inclined to occur in the grains whose <001> crystal orientation were paralleled to tensile direction. The twinning phenomenon in a hot-rolled Fe-6.5 wt.%Si [36] with equiaxed grains demonstrated that the morphology of grain boundaries is not the decisive factor on the twinning mechanism in this alloy.
Thus, the twinning can be an additional mechanism other than the disordering that can be triggered to contribute in better formability of the Fe-6.5 wt.%Si alloy. This possible deformation mechanism is of great importance for this hard and brittle material, because a much improvement in the formability of the Fe-6.5 wt.%Si alloy can be expected, e.g. both high strength and good formability can be achieved in the twinning-induced plasticity (TWIP) steels [37]. As the twinning in principle has close relationship with the grain orientation, deformation twinning might also occur in the equiaxed-grained Fe-6.5 w t.%Si bars. On the other hand, texture is often observed in as-drawn wires. It is of great interests to study the deformation behavior of the Fe-6.5 wt.%Si alloy wires.
Researchers [38,39] claimed that transformers can be constructed by coiling silicon steel wires on a copper conductor, which suggests that the high silicon steel wires with terrific soft magnetic properties have great industry application potentials. Previously, Fe-6.5 wt.%Si alloy wires with diameter of 1.6 mm were fabricated through die forging, hot rotary swaging, and hot drawing process [40].
In present work, deformation twinning and high tensile elongation were observed in the Φ6 mm hot rotary swaging bars with equiaxed grains, which can suggest much higher formability of the Fe-6.5 wt.%Si wires. We investigated the deformation characteristics, formation conditions of deformation twinning, and the effect of twinning on enhancing the ductility in the Fe-6.5 wt.%Si alloy. The microstructures and grain orientations were observed to recognize the deformation mechanism during tensile tests.
2. Material and methods
Fe-6.5 wt.%Si alloy ingots were prepared by induction melting pure iron (Fe =99.5 wt.%) and metallic silicon (Si =99 wt.%) at 1500-1600 °C in vacuum before casting into a metal mold. The chemical composition of the ingots is listed in Table 1. After homogenization at 1050 °C for 50 h, the ingots were die forged into Φ13 mm rods at 800-1100 °C. Hot rotary swaging was employed to deform the forged rods into Φ6 mm bars at 850-950 °C.
Table 1 Chemical compositions of Fe-6.5 wt.%Si alloy (wt.%).
| C | Si | Mn | S | P | Ti | B | Fe |
|---|---|---|---|---|---|---|---|
| 0.090 | 6.510 | 0.015 | 0.0009 | 0.054 | 0.005 | 0.0004 | Bal |
Heat treatments were applied on the Φ6 mm bars with various cooling methods: brine quenching (BQ), water quenching (WQ), step quenching (SQ) and furnace cooling (FC). The heat treatment parameters are shown in Table 2. The procedure of the SQ is that the heated rods were dipped into a salt bath with a temperature of 400 °C for 10 min followed by air cooling.
Table 2 Heat treatments for as-received Φ6 mm hot rotary swaging bars.
| Brine quenching (BQ) | Water quenching (WQ) | Step quenching (SQ) |
|---|---|---|
| 800 °C ×5 min | 800 °C ×5 min | 800 °C ×5 min |
| 800 °C ×10 min | 800 °C ×10 min | 800 °C ×10 min |
| 850 °C ×5 min | 850 °C ×5 min | 850 °C ×5 min |
| 850 °C ×10 min | 850 °C ×10 min | 850 °C ×10 min |
Specimens of the Φ6 mm hot rotary swaged bars before and after the heat treatments were polished and etched with a solution of 5% HNO3 in the deionized water. The microstructures of these specimens were observed with an Ernst Leitz Wetzlar optical microscope.
Tensile ductility of the specimens at intermediate temperatures was measured by DDL50 high temperature electronic universal testing machine. All the tensile tests were carried out at stretching rates of 0.42-1 mm/min and temperatures of 300-400 °C.
The crystallographic orientation of the specimens was detected by an Electron backscattered diffraction (EBSD) detector mounted on a ZEISS SUPRA 55 scanning electron microscope (SEM). The morphology and the orientation relationship between the twinning grains and the matrix were observed by a Transmission electron microscopy (TEM), using a Tecnai G2 F30. The TEM samples were prepared by ion milling.
3. Results
3.1. Heat treatments and microstructures
The grain sizes of the Φ6 mm bars before and after the heat treatments are listed in Table 3. The grains are equiaxed with an average size of 490 μm before the heat treatments. The equiaxed-grain size increases with the temperature and time. For the 5-min-annealing, the grain size increases from 490 μm to about 550 μm at 800 °C and further to about 590 μm at 850 °C. However, the SQ specimens show a significant increase (over 670 μm) in grain size when the annealing time is 10 min.
Table 3 Variation of grain sizes (μm) of the Φ6 mm Fe-6.5 wt.% Si bars with heat treatment parameters.
| Original size | Heat treatments | 800 °C ×5 min | 800 °C ×10 min | 850 °C ×5 min | 850 °C ×10 min |
|---|---|---|---|---|---|
| 490 | BQ | 556 | 544 | 580 | 600 |
| WQ | 516 | 520 | 604 | 520 | |
| SQ | 548 | 660 | 582 | 678 |
3.2. Mechanical properties
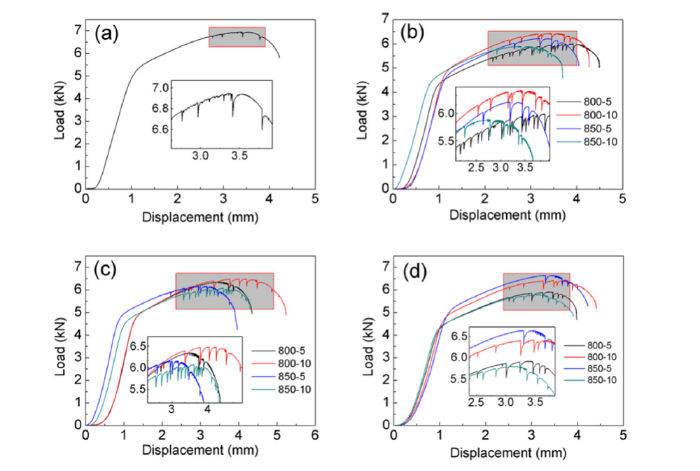
Fig. 1 shows the tensile load-displacement curves with a tensile rate of 0.42 mm/min of the Φ6mm bars after heat treatments at 300 °C. All the curves contain an elastic deformation stage, a parabola-like strain-hardening stage, and a necking stage. Importantly, all the curves exhibit discrete serration fluctuations (‒0.4 kN or ‒60 MPa) and a series of jarring sound is accompanied during the tensile tests. The serrations began to occur at stress of 959 MPa (6.8 kN) and strain of 17.3 % (2.51 mm) for the as drawn wire and at stresses of 770-890 MPa (5.4-6.3 kN) and strain of 12.6 %-15.7 % (1.83-2.28 mm) for the heat treated wires, just before the maximum stresses (or tensile stresses) were reached. More serration fluctuations appear for the specimen after the heat treatments. The yield strength and the tensile strength of the Φ6 mm Fe-6.5 %Si bars before heat treatment are respectively 763 MPa (5.4 kN) and 1013 MPa (7.2 kN) at temperature of 300 °C and strain rate of 0.42 mm/min. They correspondingly decrease into 600-700 MPa (4.2-4.9 kN) and 850-950 MPa (6.0-6.7 kN) for the annealed specimens. Therefore, a certain heat treatment can reduce the yield strength and the tensile strength of the Fe-6.5 wt.%Si alloy.
Fig. 1.
Fig. 1.
Tensile load-displacement curves of the Φ6 mm bars (a) before and after heat treatments: (b) BQ, (c) WQ and (d) SQ.
The effect of the heat treatments on the tensile elongations of the Φ6 mm bars with equiaxed grains is shown in Table 4. The elongation of the original specimen is 18 %, and it reaches about 25 % after the heat treatments, and the highest is up to 30 %. The tensile ductility of the Φ6 mm hot rotary swaging bars is enhanced after the heat treatments.
Table 4 Elongations (%) of the Φ6 mm bars before and after heat treatments.
| Original sample | Heat treatments | 800 °C ×5 min | 800 °C ×10 min | 850 °C ×5 min | 850 °C ×10 min |
|---|---|---|---|---|---|
| 18.5 | BQ | 29.4 | 21.9 | 23.5 | 21.6 |
| WQ | 20.7 | 27.3 | 24.3 | 23.5 | |
| SQ | 23.5 | 24.5 | 30.2 | 22.5 |
Fig. 2 shows the fracture morphology of the specimens before and after heat treatments. The cleavage steps and dimples exist simultaneously in the fracture before the heat treatment, as shown in Fig. 2(a). The fractures of the specimens after the heat treatments change from the cleavage fracture with cleavage steps to dimples, as shown in Fig. 2(b)-(d).
Fig. 2.
Fig. 2.
Fracture morphology of specimens (a) before and after heat treatments: (b) BQ at 800 °C × 5 min, (c) WQ at 800 °C × 10 min, and (d) SQ at 850 °C × 5 min.
3.3. Evolution of microstructures
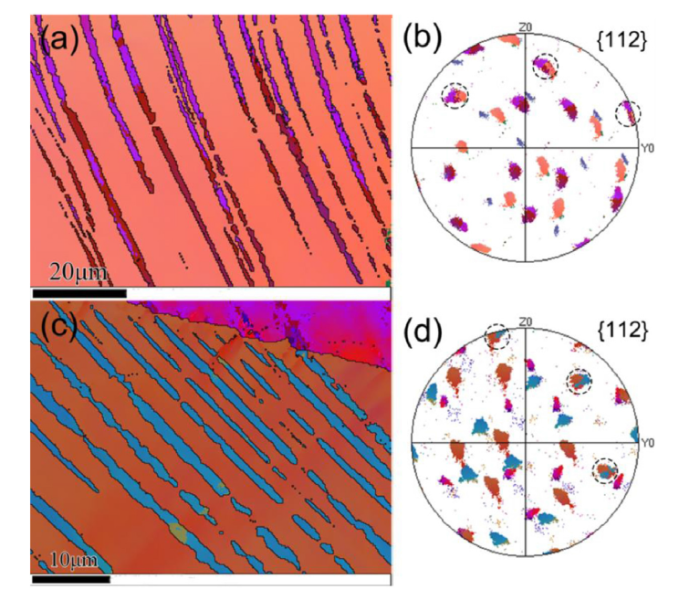
Fig. 3 shows the deformed microstructures of the Fe-6.5 wt.%Si alloy specimens (SQ and BQ, 800 °C × 10 min) after tensile tests at 300 °C. Many deformation bands appear in the equiaxed-grained specimens after the heat treatments, as shown in Fig. 3. A high density of deformation bands can be observed in the necking area (Fig. 3(a) and (c)), while a low density of deformation bands in the homogeneous deformation area (Fig. 3(b) and (d)). Fig. 4 shows orientation maps and the {112} pole figures of the deformation bands and matrix. The distinguishing orientations of the deformation bands and matrix in these specimens (SQ and BQ, 800 °C × 10 min) can be observed after the tensile tests, as shown in Fig. 4(a) and (c). Three coincident points representing the deformation bands and the matrix are obtained in the {112} pole figure, as shown in Fig. 4(b) and (d), which indicates that there exists a certain orientation relationship between the deformation bands and matrix in the {112} plane, namely {112}DB∥{112}M. Therefore, the deformation bands may be deformation twins by the analysis of the orientations between deformation bands and matrix.
Fig. 3.
Fig. 3.
Microstructures of the Fe-6.5 wt.% Si ally specimens at 300 °C after tensile after heat treatment at 800 °C × 10 min: necking area (a) and homogeneous deformation area (b) after SQ, necking area (c) and homogeneous deformation area (d) after BQ.
Fig. 4.
Fig. 4.
Orientation maps and {112} pole figures of deformation bands and matrix: orientation map (a) and pole figure (b) of a specimen with SQ after 800 °C×10 min; orientation map (c) and pole figure (d) of a specimen with BQ after 800 °C × 10 min.
4. Discussion
4.1. Deformation twinning in equiaxed-grained Fe-6.5 wt.%Si alloy
The occurrence frequency and size of the deformation twinning depend on the crystal structure and the stacking fault energy (SFE). The deformation twinning forms easily in metals and alloys with low SFE, e.g. in face centered cubic structure (FCC) metals. However, deformation twinning also occurs in metals and alloys of high SFE with body centered cubic structure (BCC) metals, such as the Fe-6.5 wt.%Si alloy at a low deformation temperature or a high deformation rate [41,42].
There are several significant results to verify the deformation bands in the rotary swaged Fe-6.5 wt.%Si bars after heat treatments to be deformation twins. The first, serrations occurred in the tensile curves, and a series of jarring are observed during the tensile tests. The second, deformation bands took place in the equiaxed grains. The third, the certain orientation relationship between the deformation bands and matrix in {112} plane is {112}DB∥{112}M.
The TEM micrographs of deformation twins in a specimen with BQ after 800 °C × 10 min are shown in Fig. 5. The thin lamellas of twins can be observed after tensile tests in bright field image (Fig. 5(a)). Certain twin boundaries are straight, and others are crooked. This was typical characteristics of the morphology of twins in bcc structure, e.g. twins in β-titanium alloy [43]. The dark field image implied that two adjacent twins usually appear together (Fig. 5(b)). The corresponding selected area electron diffraction (SAED) pattern result shows that twin and matrix have a mirror symmetry relationship with the twinning plane (2 1¯ 1), as shown in Fig. 5(c). It indicates that the twinning system is (2 1¯ 1)[11 1¯] which is one of 12 variants of the {112}<111> twinning systems.
Fig. 5.
Fig. 5.
TEM images of deformation twins in a specimen with BQ after 800 °C × 10 min: (a) Bright field image shows thin lamellas of twins; (b) Dark field image; (c) Corresponding SAED pattern with a zone axis [113]T. The subscript M stands for the matrix and T for twin.
4.2. Tension twinning Schmid factor in equiaxed-grained Fe-6.5 wt.%Si alloy
According to the reports [34,35,[44], [45], [46]], the expansion of twinning plane is the result of the glide of partial dislocations. One can use the Schmid’s law to calculate the tension twinning Schmid factor (TTSF) of each grains, so that the proportion of the grains that tend to occur twinning can be obtained. The TTSF is defined by Eq. (1):
where λ is the angle between the tension direction and the normal direction of the twinning plane, φ is the angle between the tension direction and the twinning direction. The range of the two angles is 0° to 180°, then the range of m is -0.5 to 0.5. The twinning system of BCC is {112}<111 > , and it includes twelve equivalent systems.
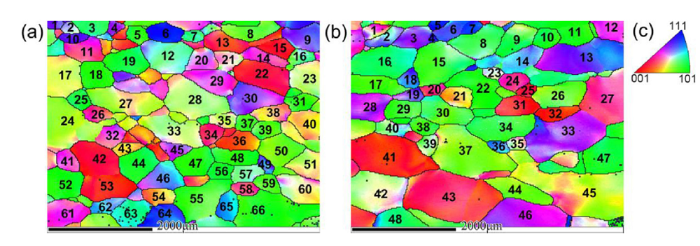
The grain orientations of the Φ6 mm bars after heat treatments (SQ and BQ, 800 °C × 10 min) are shown in Fig. 6. The rotary-swaging specimens exhibit random distribution of crystallographic orientation after SQ (Fig. 6(a)) and BQ (Fig. 6(b)). The max multiples of uniform density (MUD) of the specimen after SQ is 2.59, and another after BQ reaches 2.04. Both of them show weak <110> orientation. According to the coordinate transformation and the Euler angles obtained by the EBSD results, the highest TTSF value of the {112}<111> twinning system can be calculated. Based on the analysis of the orientation of the specimens after SQ and BQ, the Euler angles and TTSF of the equiaxed grains after SQ and BQ are listed in Table 5, Table 6.
Fig. 6.
Fig. 6.
Orientation maps of the specimens after SQ at 800 °C×10 min (a), after BQ at 800 °C×10 min (b), and corresponding legend (c) for maps.
Table 5 Euler angles and TTSF value in {112}<111> twinning system after SQ.
| Grain | Euler angles | TTSF | Grain | Euler angles | TTSF | ||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | (254.7 | 27.1 | 47.1) | 0.41 | 34 | (27.2 | 21.8 | 49.2) | 0.46 |
| 2 | (55.8 | 37.1 | 22.4) | 0.34 | 35 | (140.3 | 49.3 | 33.1) | 0.22 |
| 3 | (258.5 | 41.7 | 1.9) | 0.28 | 36 | (204.6 | 29.5 | 69.2) | 0.40 |
| 4 | (252.2 | 25.5 | 84.7) | 0.43 | 37 | (186.8 | 19.1 | 44.4) | 0.30 |
| 5 | (123.3 | 49.7 | 48.7) | 0.21 | 38 | (317.2 | 13.0 | 66.6) | 0.49 |
| 6 | (300.0 | 40.6 | 5.4) | 0.44 | 39 | (10.2 | 6.5 | 24.1) | 0.28 |
| 7 | (279.7 | 40.6 | 4.3) | 0.29 | 40 | (26.3 | 9.7 | 41.4) | 0.32 |
| 8 | (346.6 | 22.5 | 67.0) | 0.45 | 41 | (281.2 | 15.6 | 11.6) | 0.49 |
| 9 | (265.4 | 28.3 | 69.7) | 0.41 | 42 | (349.3 | 39.6 | 16.0) | 0.48 |
| 10 | (256.0 | 30.2 | 46.1) | 0.38 | 43 | (258.2 | 23.6 | 9.1) | 0.45 |
| 11 | (240.1 | 23.5 | 10.7) | 0.45 | 44 | (8.5 | 35.8 | 35.6) | 0.33 |
| 12 | (88.7 | 13.0 | 5.6) | 0.49 | 45 | (209.3 | 44.4 | 3.8) | 0.42 |
| 13 | (150.4 | 22.8 | 9.9) | 0.45 | 46 | (30.7 | 39.2 | 11.6) | 0.40 |
| 14 | (321.5 | 22.0 | 42.7) | 0.45 | 47 | (167.8 | 3.5 | 52.5) | 0.32 |
| 15 | (51.0 | 27.2 | 26.0) | 0.41 | 48 | (181.2 | 43.6 | 49.2) | 0.26 |
| 16 | (28.7 | 26.3 | 26.9) | 0.42 | 49 | (255.6 | 21.6 | 67.8) | 0.46 |
| 17 | (227.5 | 38.5 | 56.3) | 0.31 | 50 | (355.9 | 38.1 | 60.2) | 0.32 |
| 18 | (1.2 | 52.0 | 48.8) | 0.19 | 51 | (295.2 | 32.0 | 53.0) | 0.36 |
| 19 | (89.8 | 52.7 | 47.4) | 0.18 | 52 | (3.9 | 22.4 | 38.3) | 0.39 |
| 20 | (296.3 | 18.3 | 88.6) | 0.47 | 53 | (7.1 | 36.2 | 5.4) | 0.48 |
| 21 | (19.5 | 36.4 | 48.8) | 0.32 | 54 | (142.3 | 9.4 | 61.7) | 0.33 |
| 22 | (156.4 | 17.2 | 13.9) | 0.48 | 55 | (62.8 | 38.5 | 41.2) | 0.28 |
| 23 | (60.5 | 33.6 | 43.9) | 0.34 | 56 | (75.7 | 47.1 | 26.9) | 0.23 |
| 24 | (69.5 | 31.9 | 19.3) | 0.38 | 57 | (50.1 | 46.4 | 63.4) | 0.25 |
| 25 | (276.4 | 43.4 | 88.7) | 0.26 | 58 | (220.6 | 30.0 | 44.1) | 0.47 |
| 26 | (220.7 | 18.9 | 34.1) | 0.47 | 59 | (290.9 | 4.8 | 34.9) | 0.38 |
| 27 | (270.8 | 9.2 | 64.2) | 0.50 | 60 | (339.9 | 26.7 | 44.5) | 0.41 |
| 28 | (134.3 | 43.8 | 26.8) | 0.28 | 61 | (125.8 | 23.4 | 74.3) | 0.45 |
| 29 | (27.1 | 36.4 | 42.4) | 0.31 | 62 | (206.2 | 40.6 | 33.2) | 0.40 |
| 30 | (321.2 | 31.8 | 64.4) | 0.38 | 63 | (207.2 | 31.8 | 24.1) | 0.38 |
| 31 | (235.3 | 1.4 | 86.2) | 0.48 | 64 | (279.9 | 41.6 | 24.9) | 0.43 |
| 32 | (55.1 | 29.1 | 21.7) | 0.40 | 65 | (290.5 | 25.0 | 20.3) | 0.43 |
| 33 | (104.4 | 29.6 | 84.0) | 0.40 | 66 | (193.0 | 17.2 | 34.2) | 0.30 |
Table 6 Euler angles and TTSF value in {112}<111> twinning system after BQ.
| Grain | Euler angles | TTSF | Grain | Euler angles | TTSF | ||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | (224.6 | 24.2 | 25.8) | 0.44 | 25 | (208.1 | 11.3 | 43.5) | 0.50 |
| 2 | (318.3 | 34.8 | 71.0) | 0.33 | 26 | (197.1 | 22.9 | 41.4) | 0.37 |
| 3 | (219.1 | 41.4 | 54.7) | 0.41 | 27 | (210.9 | 31.1 | 51.0) | 0.45 |
| 4 | (81.1 | 43.2 | 60.6) | 0.43 | 28 | (303.7 | 21.6 | 78.3) | 0.46 |
| 5 | (254.3 | 38.4 | 69.4) | 0.42 | 29 | (187.9 | 51.8 | 47.5) | 0.19 |
| 6 | (73.4 | 24.4 | 53.7) | 0.44 | 30 | (179.5 | 36.9 | 57.1) | 0.33 |
| 7 | (73.1 | 30.5 | 64.5) | 0.4 | 31 | (32.1 | 28.2 | 68.0) | 0.45 |
| 8 | (234.3 | 46.7 | 36.0) | 0.24 | 32 | (183.3 | 12.9 | 3.0) | 0.43 |
| 9 | (93.0 | 42.4 | 77.5) | 0.28 | 33 | (222.7 | 38.2 | 25.9) | 0.40 |
| 10 | (290.9 | 51.5 | 48.6) | 0.19 | 34 | (12.6 | 33.8 | 27.9) | 0.36 |
| 11 | (354.3 | 33.9 | 46.3) | 0.30 | 35 | (248.6 | 26.8 | 14.0) | 0.40 |
| 12 | (240.6 | 20.3 | 54.3) | 0.47 | 36 | (110.3 | 23.7 | 27.4) | 0.44 |
| 13 | (302.8 | 29.9 | 81.1) | 0.42 | 37 | (175.9 | 15 | 63.2) | 0.41 |
| 14 | (65.7 | 33.4 | 41.8) | 0.4 | 38 | (265.3 | 36 | 4.6) | 0.34 |
| 15 | (16.0 | 22.6 | 37.6) | 0.45 | 39 | (14.2 | 52.5 | 49.3) | 0.19 |
| 16 | (137.3 | 14.5 | 85.5) | 0.42 | 40 | (197.7 | 36.4 | 43.0) | 0.30 |
| 17 | (358.9 | 36.9 | 37.1) | 0.29 | 41 | (180.3 | 16.4 | 80.2) | 0.48 |
| 18 | (48.1 | 28.7 | 83.9) | 0.41 | 42 | (139.8 | 44.1 | 42.2) | 0.23 |
| 19 | (79.4 | 29.6 | 35.4) | 0.40 | 43 | (33.9 | 36.6 | 5.9) | 0.42 |
| 20 | (35.9 | 19.0 | 39.2) | 0.47 | 44 | (183.0 | 44.7 | 57.6) | 0.26 |
| 21 | (34.6 | 19.5 | 42.3) | 0.39 | 45 | (139.0 | 42.7 | 34.3) | 0.35 |
| 22 | (58.4 | 48.5 | 40.7) | 0.19 | 46 | (79.6 | 29.3 | 36.8) | 0.42 |
| 23 | (65.7 | 33.4 | 41.8) | 0.34 | 47 | (13.8 | 29.2 | 35.0) | 0.39 |
| 24 | (235.6 | 20.7 | 23.1) | 0.46 | 48 | (249.9 | 47.6 | 42.0) | 0.22 |
TTSF is defined similarly to that of the slip. Higher TTSF value often implies a lower stress required for twinning. In another words, the grain whose TTSF value is positive and large has high possibility of twinning and favorably leads to tensile deformation. The grain whose TTSF value is negative favorably leads to contraction along the tensile direction and the twins cannot be observed during the tensile test. The percentage of the grains with high TTSF value (>0.4, bold fonts with underline) after SQ and BQ is above 50 % as listed in Table 5, Table 6. The high TTSF values (>0.4) of the grains indicate that twinning is very likely to occur during the tensile deformation.
The equiaxed-grained specimens of the Fe-6.5 wt.%Si alloy slide at first during the tensile tests, appearing work hardening and forming some places of stress concentration, which prepares for the deformation twinning. With the increase of deformation, the grains slip become difficult and twinning starts for further deformation (Fig. 1). The inhomogeneous plastic deformation indicates an inhomogeneous stress distribution in the Fe-6.5 wt.%Si alloy specimens. Deformation twinning occurs at places of the high stress concentration. Finally, the excessive stress leads to necking down formation and fracture. Therefore, a high density of deformation twins occurs in the necking area, while a low density of twins arises in other places, as shown in Fig. 3.
4.3. Influencing factors on deformation twinning in Fe-6.5 wt.%Si alloy
Many variables may influence deformation twinning behavior such as temperature, strain rate, grain size, ordered phases or crystal orientation, etc. [47]
4.3.1. Effects of temperature and tensile rate
The effect of the temperature on the BCC metals is very evident. The load and stress increase a lot with decreasing temperature during deformation. The flow stress may ultimately reach the twinning stress by work-hardening, and the deformation mechanism transforms from slip to twinning. Fig. 7 shows the tensile load-displacement curves of the Φ6 mm bars with heat treatment (BQ, 800 °C × 10 min) at the temperature of 300-400 °C and the stretching speed of 0.42-1 mm/min. The load (6.5-7.2 kN) and flow stress (920.0-1019.1 MPa) are higher at 300 °C than those (the load value 5.2-6.5 kN, the stress value 736.0-920.0 MPa) at 400 °C. Furthermore, when twinning occurs, the deformation (1.09-1.77 mm) and strain (7.5 %-12.2) are lower at 300 °C than those (2.10-2.90 mm, 14.5 %-20) at 400 °C, as shown in Fig. 7. Twinning occurs more easily at lower temperature (300 °C).
Fig. 7.
Fig. 7.
Tensile load-displacement curves of Φ6 mm bars after BQ at 300 °C (a) and at 400 °C (b).
The high strain rate and low temperature are certainly effective for twinning. However, twinning stress changes rather slowly with temperature but is very sensitive to the strain rate [47,48]. When a twin forms, a certain stress relaxation occurs, with a fluctuation on the tensile load-displacement curve or the stress-strain curve [41]. There are more discrete serrations at a stretching speed of 1 mm/min and at 300 °C and 400 °C, that is, larger number of twins appear at higher stretching speed (1 mm/min), as shown in Fig. 7. The twinning stress decreases with increasing strain rate, meanwhile, work hardening is more likely to be caused. Both of them create conditions for twinning.
4.3.2. Effect of grain size
Longer period of heat treatments, the parameters of which are shown in Table 7, were applied on the as swaged Φ6 mm Fe-6.5 wt.%Si bars in order to increase the grain size. Fig. 8 shows the tensile load-displacement curves of these heat-treated bars. The tensile tests were performed at 300 °C and the strain rate was 0.42 mm/min.
Table 7 Heat treatments of Φ6 mm bars.
| Cooling methods | Technical parameters | |||
|---|---|---|---|---|
| Brine quenching (BQ) | 800 °C ×10 min | 800 °C ×1 h | 800 °C ×5 h | 800 °C ×10 h |
| Furnace cooling (FC) | 800 °C ×10 min | 800 °C ×1 h | 800 °C ×5 h | 800 °C ×10 h |
Fig. 8.
Fig. 8.
Tensile load-displacement curves of Φ6 mm bars after heat treatments of BQ (a) and FC (b).
The critical load or stress when twins appear is called the twinning load or stress. The twinning load (stress) are 5.842 kN (826.5 MPa), 6.081 kN (860.3 MPa), 6.134 kN (867.8 MPa), and 6.296 kN (890.7 MPa) for the BQ specimens of 10 min, 1 h, 5 h and 10 h at 800 °C, as shown in Fig. 8(a) respectively.
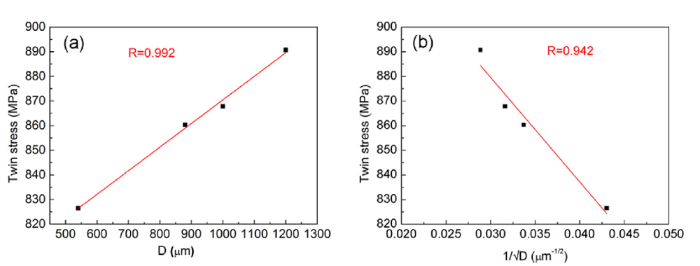
After the heat treatment of BQ, the grain sizes increase (540 μm, 880 μm, 1000 μm and 1200 μm) with the annealing time. Fig. 9 shows the relationship between the twinning stress and the grain size. The data fits a linear relationship which is proportional, as shown in Fig. 9(a). The influence of grain size on the twinning stress in the Fe-6.5 wt.%Si alloy indicates that the twinning stress increases with increasing of the grain size, while it disobeys the Hall-Petch type relationship, as shown in Fig. 9(b).
Fig. 9.
Fig. 9.
Relationship between twin stress and grain size: D (a) and 1/√D (b). D represents grain diameter.
The yield stress and twinning stress in 3% silicon iron [49] and chromium [50] obey the Hall-Petch relationship. Previous reports [51,52] suggested that the twinning stress was found to increase with grain size decreasing in a TWIP steel. However, the effect of grain size on the twinning stress in the Fe-6.5 wt.%Si alloy indicates that the twinning stress increases with the grain size, and disobeys the Hall-Petch type relationship. The reason why the results do not follow the Hall-Petch type relationship is that the influence factors on mechanical property of the Fe-6.5 wt.%Si alloy are not only grain size and grain orientation, but also the ordered phases. Importantly, compared with the grain size and orientation, the ordered phases like B2 and DO3 are more influential on mechanical property of the Fe-6.5 wt.%Si alloy. Besides, the crystal structure modes of the B2 phase and DO3 phase are superlattices, whose effects on the ductility of Fe-6.5 wt.%Si alloy are more intricate. All the factors can influence the twinning stress.
4.3.3. Effect of ordered phase
There are ordered structures like B2 and DO3 existing in Fe-6.5 wt.%Si alloy, and a higher cooling rate after annealing often results in a lower degree of order, which is always manifested as smaller ordered domain size [36,53,54]. The formation of DO3 phase and the growth of B2 can be largely suppressed by rapid cooling, and the formation of ordered phases can be promoted by slow cooling [28]. The SAED patterns parallel to <110> zone axes and corresponding dark images of the samples after the heat treatment (800 °C × 10 h) of FC and BQ are shown in Fig. 10. In the SAED patterns, the B2 domains can be observed using the superlattice reflection (200), indicated by arrow A, and the DO3 domains can be observed using the superlattice reflection (111) [28], indicated by arrow B. After the heat treatment of FC, there exist B2 and DO3 (Fig. 10(a)), the B2 ordered domain size is 1000-2000 nm (Fig. 10(b)), and the DO3 ordered domain size is 30-60 nm (Fig. 10(c)). After BQ, there only exists B2 spot (Fig. 10(d)), and the B2 ordered domain size decreases to 50-100 nm. Therefore, the B2 ordered domain size decreases and DO3 phase is refrained after the heat treatment of BQ, indicating the volume fraction and the degree of ordering of the samples after BQ is lower than that after FC.
Fig. 10.
Fig. 10.
TEM micrographs before deformation of the samples after heat treatment of FC and BQ.
After FC: (a) SAED patterns along [011] zone axis, Arrow A designates (200), and arrow B designates (111); (b) Dark field image obtained using (200) spot with arrows designating anti-phase boundary (APB); (c) Dark field image obtained using (111) spot.
After BQ: (d) SAED patterns along the [011] zone axis; (e) Dark field image obtained using (200) spot.
Accordingly, with lower volume fraction of ordered phases after BQ, WQ and SQ, the curves exhibit more discrete serrations (Fig. 1), i.e. more twins occur. With higher volume fraction of ordered phases after FC, deformation twinning is suppressed, as shown in Fig. 8(b). The results show that ordered phases like B2 and DO3 restrain the twinning formation. Cahn and Coll [55] found that alloys with less than 50 % long range order formed twins, but that deformation twinning was suppressed in more highly ordered alloys. Thus, the ordering content and degree of order hinder twinning.
4.4. Mechanism of deformation twinning in Fe-6.5 wt.%Si alloy
There are some affecting factors on the deformation twinning. On the one hand, a lower temperature and higher strain rate accelerate the work hardening, promoting the twinning formation. On the other hand, the increasing ordered phases enhanced the lattice resistance, repressing the twinning formation. However, the effect of grain size on the twinning formation is not noticeable, the relationship between twinning stress and grain size is not satisfied with the Hall-Petch equation. In addition, the tensile ductility of the equiaxed-grained Fe-6.5 wt.%Si alloy bars is enhanced when the deformation twinning occurs. Deformation twinning can be employed to promote the production of the Fe-6.5 wt.%Si alloy sheets and wires [35].
Deformation twinning results from a homogeneous shearing of the matrix by a highly coordinated glide of partial dislocations with the same Burgers vector, with exactly one dislocation gliding on each successive {112}-type twinning plane (BCC structure). The required stress of deformation twinning is commonly higher than that of dislocation slip, so the slip occurs first during a deformation. As the slip is obstructed, deformation twinning appears at the places of high stress concentration [41,47]. The tensile curves (Fig. 1) show that twinning occurred after a sufficient work hardening.
Moreover, the columnar grained Fe-6.5 wt%Si samples from direction solidification [34,35], the equiaxed-grained Fe-6.5 wt.%Si samples from hot rolling [36] and rotary swaging (this work) indicate that the high TTSF value of the grains can provide necessary condition for the formation of deformation twins. The TTSF values of more than half of the grains in the samples of this work are high (as discussed in Section 4.2). Therefore, the deformation twins can be much easier to form in the Fe-6.5 wt.%Si alloy with BCC structure after swaging and heat treatments. Further effort to improve the formability of the Fe-6.5 wt.%Si can be devoted into the study to form favorable grain orientation with high TTSF value.
5. Conclusions
In this work, the tensile tests at various temperatures and strain rates were carried out, and the microstructures and grain orientation were observed to investigate the deformation mechanism. Besides, the effects on the deformation mechanism were also studied. Based on these results, the following conclusions can be drawn:
(1)The tensile ductility of the Φ6 mm equiaxed-grained Fe-6.5 wt.%Si alloy bars enhanced at intermediate temperatures. Meanwhile, the yield strength and the tensile strength of the Fe-6.5 wt.%Si alloy were lower after the heat treatments.
(2)Deformation twinning occurred in the equiaxed grains at intermediate temperatures during tensile tests, and a large number of twins appeared after the heat treatments, which can improve the tensile ductility of the equiaxed-grained Fe-6.5 wt.% Si alloy bars. More deformation twins occurred in the necking area than other places.
(3)The deformation twins are easily to form in the grains with high tension twinning Schmid factor value, and the number of such grains in the samples after rotary swaging and heat treatment is above 50 %.
(4)The higher temperatures, lower strain rates and larger degree of order can suppress the formation of deformation twinning. The grain sizes had little effect on deformation twinning. The influence of grain sizes on twinning stress disobeyed the Hall-Petch equation.
Acknowledgments
This work was financially supported by the National Natural Science Foundation of China (Nos. 51471031 and U1660115) and the State Key Laboratory for Advanced Metals and Materials (No. 2016Z-17).
Reference
Study on New Processing Technology, Structure and Properties for Boron-doped Fe-6.5wt%Si Alloy Sheets
The phonon approach and the Debye model are combined to predict the vibrational thermodynamic contribution for the following Fe-Si compounds: Fe3Si, Fe2Si, Fe5Si3, FeSi, beta-FeSi2 and alpha-FeSi2. Both the ultrasoft pseudopotential (USPP) and the projector augmented wave (PAW) methods are employed to describe the electron-ion interactions. The generalized gradient approximation including PW91 and PBE is employed to describe the exchange-correlation functional. Lattice parameters, bulk modulus, phonon dispersions, and finite temperature thermodynamic properties are calculated and compared with available experimental data, and good agreement is observed. The thermodynamic data obtained in the present work provide better understanding of the stability of binary Fe-Si compounds and can be used for further thermodynamic modeling of this system. (C) 2011 Elsevier Ltd.
5th International Conference on Magnetism and Metallurgy, Ghent
fiber texture at intermediate temperatures (300-500 degrees C) was investigated. Compared with equiaxed-grained Fe-6.5wt.%Si alloy, the enhanced tensile ductility and its mechanism of columnar-grained Fe-6.5wt.% Si alloy were mainly studied by the analysis of tensile twinning Schmid factor value and the deformation microstructure. The results showed that tensile ductility of the Fe-6.5wt.%Si alloy with columnar grains were increased significantly, i.e., the elongation of the columnar-grained specimens were increased to 6.6% (300 degrees C), 51.1% (400 degrees C), 51.3% (500 degrees C), which, respectively, corresponded to an increase of 3.7%, 25.8% and 23.2% compared with that of the equiaxed-grained specimens. The analysis of tensile twinning Schmid factor value and the deformation microstructure both demonstrated that deformation twinning occurred locally in the equiaxed-grained Fe-6.5wt.%Si alloy, while a great number of twins formed homogeneously in the columnar-grained Fe-6.5wt.%Si alloy. The significant enhancement of tensile ductility of the columnar-grained Fe-6.5wt.%Si alloy at intermediate temperatures was mainly ascribed to the formation of a great number of homogeneous deformation twins. (C) 2011 Elsevier Ltd.]]>
Transformer with Magnetic Core of Coiled Wires
Improvement and Modifications to Electrical Transformers for Any Application and Power
AbstractThe active twin variants during {10–12} twinning of magnesium alloys were dependent on the strain path (i.e., compression perpendicular to the c-axis or tension parallel to the c-axis), and their section mechanism was governed by the Schmid law. The activation of specific twin variants depending on the strain path induced a significant difference in twinning characteristics, such as twin morphology, volume fraction of twins with strain, and twin texture, and consequently gave rise to a totally different effect on the deformation. The differences in the deformation characteristics (flow stress and strain hardening) between both strain paths are explained in relation to activation stresses for twinning and slips, activities of twinning and slips in the deformation, the Hall–Petch effect by twinning-induced grain size change, and twinning-induced change in activities of slips.]]>
AbstractThe evolution of twinning and texture in two Mg-based (+Al, Mn, Zn) alloys was investigated using uniaxial tension, uniaxial compression and ring hoop tension testing at temperatures from ambient to 250 °C and a strain rate of 0.1 s−1. The results indicate that the initial extrusion texture plays an important role in the formation of different types of twins and that the twinning behavior also depends on the strain path. Contraction and double twinning are the dominant twinning mechanisms in uniaxial tension, while extension twinning prevails in uniaxial compression and ring hoop tension testing. Schmid factor analysis indicates that only components that are favorably oriented (i.e., with the highest SF values) can undergo rapid and complete twinning. The different twinning behaviors are shown to be responsible for the sharply contrasting strain hardening characteristics of the experimental flow curves and dramatic texture changes.]]>
Ye Feng











 WeChat
WeChat