A Diagram for Glass Transition and Plastic Deformation in Model Metallic Glasses

Cite this Article

Gao X.Q., Wang W.H., Bai H.Y.. A Diagram for Glass Transition and Plastic Deformation in Model Metallic Glasses. Journal of Materials Science & Technology, 2014, 30(6): 546-550 Copy to clipboard

Permissions

A Diagram for Glass Transition and Plastic Deformation in Model Metallic Glasses

Gao X.Q., Wang W.H.^*, Bai H.Y.^*

Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China

Corresponding authors. Prof., Ph.D.; Tel.: +86 10 82649198; Fax: +86 10 82640223

Abstract

In this paper, we report a strain rate related glass transition in model SrCaYbMg(Li)Zn(Cu) metallic glasses at room temperature. A critical strain rate, equivalent to glass transition temperature, is found for the strain rate induced glassy state to liquid-like viscoplastic state translation. The results show that the observation time, equivalent to temperature and stress, is a key parameter for the transition between the glass and supercooled liquid states. A three-dimension glass transition diagram involved in time, temperature and stress in metallic glasses is established.

Keyword: Homogeneous plastic flow; Glass transition; Metallic glass

Show Figures

1. Introduction

Metallic glasses (MGs) with atomic randomly packing structure, excellent glass-forming ability and wide supercooled liquid temperature region are model system for studying the fundamental issues in glass field^{[1], [2], [3], [4], [5] and [6]}. Glasses are regarded as liquids that have lost their flow ability. Generally, it is recognized that the glass transitions between supercooled liquid and glassy states in metallic glasses (MGs) are induced by thermalization or by applied stress^{[7], [8], [9], [10], [11], [12] and [13]}. Through simulation, Guan et al. ^[12] quantified the intimate coupling of temperature and shear stress in glass transition. In fact, the glass transition is observation time dependent ^[9]. For polymer glasses, their responses to stress can be observed both within a short time at high temperature and a sufficient long time at low temperatures, which is time-temperature superposition principle ^[14]. The physical similarity among MGs, colloidal and polymer glasses suggests that the glass transition in MGs could have the similar response to the key parameters of temperature ( T), stress as well as the observation time.

However, little work has been done on the effects of observation time on glass transition in MGs. This is because the MGs normally have high flow energy barrier below glass transition temperature ( T_g), and the homogeneous deformation of MGs generally is only observed at high T or in inaccessible long time scale under stress at low T^{[15] and [16]}. For example, for Zr-based MG with a flow activation energy ∼1.3 eV, the room temperature (RT) uniaxial compression at 80% of its yield stress for 5 h only leads to homogeneous flow with irreversible strain of ∼2.0 × 10^-4 ^[17]. The long time scale and very small homogeneous flow strain at low T make the study of the effects of strain rate and observation time on glass transition very difficult. Recently, some MGs such as Ce-, La- and Sr-based with low T_g have been developed^{[18], [19], [20] and [21]}. Remarkable liquid-like homogeneous flow near room temperature and under relatively high strain rates can be realized in the Sr-based glasses due to their very low flow activation energy^{[18] and [22]}. Importantly, the supercooled liquid state of the MGs can be realized solely by the homogeneous mechanical behavior, which provides a model system to study the roles of strain rate or observation time in glass transition, and to test the concept of glass transition diagram in MGs.

In this work, we report that the glass to supercooled liquid state transition can be solely induced by the strain rate $\dot{γ}$ in the model SrCaYbMg(Li)Zn(Cu) MG systems. We examine the role of $\dot{γ}$ , which is equivalent to the observation time, in the glass transition induced by stress of the MGs, and a time involved glass transition diagram is obtained. The results show that the observation time, temperature and stress can be incorporated into a generalized description of transition between glass and supercooled liquid states in MGs.

2. Experiments

Cylindrical specimens of Sr₂₀Ca₂₀Yb₂₀Mg₂₀Zn₂₀, Sr₂₀Ca₂₀Yb₂₀Mg₂₀Zn₁₀Cu₁₀, Sr₂₀Ca₂₀Yb₂₀(Li_0.55Mg_0.45)₂₀Zn₂₀ MGs of 2 mm in diameter were prepared by copper mold casting method ^[22]. The T_g and shear modulus G of the MGs were presented in . Compression tests at RT were conducted on these MGs with a length-to-diameter ratio of 2 at different applied strain rates on an Instron 3384 machine (Norwood, MA). The temperature of the compression tests was controlled by a thermocouple and the tests were performed in pure Ar atmosphere to avoid the oxidation. The X-ray diffraction results showed that the temperature in the range of 310–350 K for compression tests did not induce the crystallization. The scanning electron microscopy (SEM) was conducted in a Philips XL30 instrument. According to the shear cooperative model ^[23], the barrier energy of plastic flow units W_STZ (also termed as shear transformation zones (STZs)) in MGs can be estimated by ^[24] W_STZ∝0.4 GV_m, where V_m is average molar volume. These MGs have ultra low G (see ), and their flow barrier energy W_STZ is estimated to be 0.79, 0.75, and 0.52 eV, respectively. Clearly, these MGs have much lower activation energy of flow units compared with that of conventional MGs ^[24] and the activation of flow units is then much easier. We then could realize the homogenous flow or glass to supercooled liquid transition near RT in the MGs by stress in reasonable observation time scale, and characterize the effect of time on glass transition through their homogeneous mechanical behavior.

Table 1. Values of T_g, shear modulus G, compression yield strength σ_y, the maximum flow stress σ_max and steady flow stress σ_flow at the critical strain rate, the experimental critical strain rate

{\dot{γ}}_{g}

and the calculated critical strain rate

{\dot{γ}}_{g}^{cal}

of MGs

Sr₂₀Ca₂₀Yb₂₀Mg₂₀Zn₂₀	Sr₂₀Ca₂₀Yb₂₀Mg₂₀Zn₁₀Cu₁₀	Sr₂₀Ca₂₀Yb₂₀(Li_0.55Mg_0.45)₂₀Zn₂₀
T_g (K)	353	351	319
G (MPa)	8.89	9.47	6.28
σ_y (MPa)	452.1	433.6	375.1
σ_max (MPa)	473.6	450.3	411.9
σ_flow (MPa)	366.9	416.2	249.3
${\dot{γ}}_{g}$ (s^-1)	1 × 10^-6	5 × 10^-7	2 × 10^-4
${\dot{γ}}_{g}^{cal}$ (s^-1)	1.51 × 10^-6	1.45 × 10^-6	1.25 × 10^-4

{\dot{γ}}_{g}

and the calculated critical strain rate

{\dot{γ}}_{g}^{cal}

of MGs

3. Results and Discussion

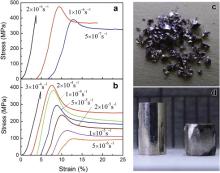
Fig. 1 shows the compressive stress–strain curves at different applied strain rates for as-cast rods of Sr₂₀Ca₂₀Yb₂₀Mg₂₀Zn₂₀ ( Fig. 1(a)) and Sr₂₀Ca₂₀Yb₂₀(Li_0.55Mg_0.45)₂₀Zn₂₀ ( Fig. 1(b)). For both of the MGs, at RT and above a critical strain rate ${\dot{γ}}_{g}$ , the true stress–strain curves exhibit an elastic loading region followed by catastrophic failure into small pieces without any plastic deformation (see Fig. 1(c)). The fracture approaches the ideal brittle behavior ^[25], which indicates that at RT the MG is in glassy state. However, below a critical strain rate ${\dot{γ}}_{g}$ , remarkably, the MGs displays a stress overshoot which is often observed in the supercooled liquid state of MGs at high T (e.g. for Zr-based MGs, the superplastic flow occurs above 600 K ^[15]). The stress overshoot is due to the structural evolution (i.e. accumulation of free volume) accompanied by softening^{[25] and [26]}. Due to the intrinsic relaxation, the stress attains a steady state after the overshoot ( Fig. 1(a and b)) which is a typical feature of homogeneous flow in glass-forming liquid. As shown in Fig. 1(d), the MGs can be deformed to 50% of its original height without observable cracking and shear banding, and further deformation is still possible, implying the significant homogeneous flow of the MG at RT. This means the metallic glasses transform into supercooled liquid state at RT by strain rate, that is the strain rate induced glass transition. To confirm the homogeneous deformation at RT, we examined the surface of the heavily deformed MG to see if there exist nano-scale shear bands. Fig. 2(a and b) shows the SEM images of the compressed sample with a strain of ε ≈ 50%. Although some oxidation spots appear, the severely deformed specimen almost keeps the smooth surface of the as-cast state and no primary shear bands and other observable shear bands can be found. The results confirm that the liquid-like homogeneous flow, similar to that observed in supercooled liquid in conventional MGs at high T, can be realized solely by $\dot{γ}$ at RT in the MGs.

	Figure Option View Download New Window
	Fig. 1. Compressive stress–strain curves at different strain rates of (a) Sr₂₀Ca₂₀Yb₂₀Mg₂₀Zn₂₀ and (b) Sr₂₀Ca₂₀Yb₂₀(Li_0.55Mg_0.45)₂₀Zn₂₀ MGs; (c) pictures of brittle behavior above ${\dot{γ}}_{g}$ and (d) homogeneous deformation behaviors (about 50% deformed) below the critical strain rate for Sr₂₀Ca₂₀Yb₂₀Mg₂₀Zn₂₀ MG.

Figure Option
View Download New Window

Fig. 2. (a) Macroscopic and (b) microscopic SEM image of about 50% heavily deformed Zn₂₀Ca₂₀Sr₂₀Yb₂₀(Li_0.55Mg_0.45)₂₀ MG. No shear bands and micro cracks can be found, indicating the homogeneous deformation of the glass. (c) The diagram of brittle to homogeneous flow translation induced by strain rate in the MG, plotting the maximum yield stress vs. the applied strain rate during compression. A well-defined transition from supercooled liquid state to glassy state can be found as

\dot{γ}

reached a constant value. And a critical strain rate

{\dot{γ}}_{g}

, which is equivalent to T_g exists. The curves are guide to the eyes.

Similar to the T dependence of the homogenous deformation in supercooled liquids, a strain rate dependent homogeneous flow can be clearly seen in the MG below ${\dot{γ}}_{g}$ (see Fig. 1(b)). When the $\dot{γ}$ decreases, the yielding stress and steady flow stress decrease. The $\dot{γ}$ dependence of the steady state flow stress ( σ_flow) corresponds to the non-Newtonian flow. At relatively low strain rates, the rate of free volume annihilation gradually comes to match that of production, and a steady state condition is eventually achieved^{[25] and [26]}. Meanwhile, the overshoot peak stress (or the maximum flow stress σ_max) decreases monotonically from ∼400 MPa to ∼100 MPa as $\dot{γ}$ decreased from 2 × 10^-4 to 5 × 10^-6 s^-1 in the homogeneous deformation region, and the peak stress almost disappeared when $\dot{γ}$ = 5 × 10^-6 s^-1. The variation tendency of the steady state stress is similar to that of the overshoot peak stress, which is a typical homogeneous flow behavior in supercooled liquid state. The results clearly illustrate the similar roles of $\dot{γ}$ and T in the homogeneous flow ^[15].

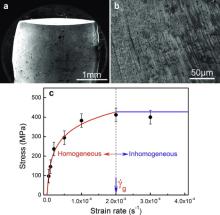
Fig. 2(c) shows the maximum stress as a function of $\dot{γ}$ ranging from 5 × 10^-6 to 3 × 10^-4 s^-1 in Sr₂₀Ca₂₀Yb₂₀(Li_0.55Mg_0.45)₂₀Zn₂₀ and actually illustrates the glassy state (brittle) to liquid-like state (homogeneous flow) translation induced by strain rate. The σ_max monotonically increases with the increasing of $\dot{γ}$ in homogeneous regime, and in glassy state $\dot{γ}$ reaches a plateau of maximum stress. A well-defined transition from supercooled liquid state to glassy state can be seen as $\dot{γ}$ reaches a critical value of ${\dot{γ}}_{g}$ = 3 × 10^-4 s^-1 (as indicated in Fig. 2(c)). The critical value ${\dot{γ}}_{g}$ , which is equivalent to T_g in temperature induced glass transition, is the intrinsic parameter characterizing the glass translation induced by strain rate or action time.

The relationship of apparent viscosity η of homogeneous flow, $\dot{γ}$ and the flow stress σ_flow can be expressed as^{[27] and [28]}: $\dot{γ} = σ_{flow} / 3 η$ . The dynamical definition of glass transition is that the viscosity of the supercooled liquid reaches ∼10¹³ Pa s^{[29] and [30]}. We then estimate the critical strain rate ${\dot{γ}}_{g}^{cal}$ by $\dot{γ} = σ_{max} / 3 η$ (The σ_max is close to yield strength). The estimated values of ${\dot{γ}}_{g}^{cal}$ , as listed in , are very close to the experimental determined values for these MGs. Meanwhile, from , one can see that the MG with larger T_g has smaller ${\dot{γ}}_{g}$ , which indicates that the T_g correlates well to ${\dot{γ}}_{g}$ for these MGs. This further confirms that $\dot{γ}$ , equivalent to temperature, is another key parameter to describe the glass transition.

Maxwell firstly extrapolated the relation between liquid and solid behavior, and proposed the relation between the viscosity and relaxation time τ as: τ = η/ G_∞, where G_∞ is the instantaneous shear modulus. The Maxwell relaxation time τ provides a key to understanding the glass transition^{[31] and [32]}. The general property of the relation indicates that liquid is solid-like on time scales much shorter than τ, and on a sufficiently long time scale any glass behaves like a liquid. The glass transition is observation time dependent, and difference between glasses and fluid liquid can be defined by a nondimensional number of the so-called Deborah number^{[31] and [32]}: D = t_r/ t_o, where t_r is the time of relaxation, and t_o is the time of observation. If t_o is very large, the glass flowing can be seen. On the other hand, if t_r >> t_o, the liquid is a glassy solid. A viscous liquid can be viewed as solid which flows in enough short time scale, and a glass can be regarded as viscous liquid in enough large time scale ^[32]. Actually, the inverse strain rate is related to action time scale of strain or stress on MGs, and is equivalent to the experimental observation time, and the effect of the strain rates on the glass transition is equivalent to that of the observation time on glass transition.

To determine the relation between the time scale, temperature and stress in glass transition process of MGs, we studied the relation between maximum yield stress and inverse strain rate at RT. Fig. 3(a) shows the σ_max vs. $\dot{γ}$ in the MG. When the liquid-to-glass transition occurs, the σ_max decreases with the extending observation time, but apparently not in a linear fashion. According to the general steady state flow theory ^[33], the relation between the σ and $\dot{γ}$ is given by^{[34] and [33]},

$\dot{γ} = 2 c_{f} v_{D} \exp (- \frac{Δ G^{m}}{k T}) \sinh (\frac{σ V}{2 \sqrt{3} k T})$ (1)

where ν_Dis the Debye frequency, Δ G^mis the activation free energy of defect migration, Vis the activation volume and kis Boltzmann constant. At a given temperature of RT, the ν_D,Δ G^mand Vare constant, and the relation between the σ_maxand $\dot{γ}$ is^{[33] and [34]},

${\dot{γ}}^{- 1} = {\dot{γ}}_{0}^{- 1} \sinh^{- 1} (a σ_{max})$ (2)

where ${\dot{γ}}_{0} = 2 c_{f} v_{D} \exp (- Δ G^{m} / k T)$ and $a = V / 2 \sqrt{3} K T$ . The line in Fig. 3(a) fits well the relation between inverse strain rate and σ_maxwithin the error. This indicates the shape of the phase boundary between stress and reverse strain rate in glass transition diagram should be a concave curvature.

	Figure Option View Download New Window
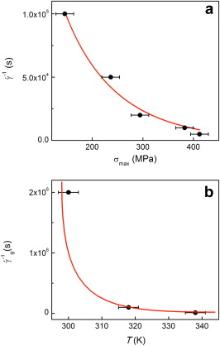	Fig. 3. (a) Maximum yield stress vs. the inverse strain rate in the Sr₂₀Ca₂₀Yb₂₀(Li_0.55Mg_0.45)₂₀Zn₂₀ MG. (b) Temperature vs. ${\dot{γ}}_{g}$ for Sr₂₀Ca₂₀Yb₂₀Mg₂₀Zn₁₀Cu₁₀ MG. The curves are guide to the eyes.

Fig. 3(b) shows the relation of T and ${\dot{γ}}_{g}$ during glass transition for Sr₂₀Ca₂₀Yb₂₀Mg₂₀Zn₁₀Cu₁₀ MG. The ${\dot{γ}}_{g}$ is 5 × 10^-7, 1 × 10^-5 and 8 × 10^-5 s^-1 at 300, 323 and 343 K, respectively. This indicates that much longer observation time, depending on the system relaxation time, is needed to observe the viscoplastic flow in MG at lower T. For the MGs with high T_g, the relaxation process is extremely sluggish at RT, and the observation time has to be extended too long time scale for observing the glass transition, the homogeneous flow is inconspicuous or even not be experimentally achieved at RT. This is confirmed in Zr-based MG with higher flow activation energy. The homogeneous viscous flow with irreversible strain at RT by uniaxial compression is observable only when $\dot{γ}$ is less than ∼10^-10 s^-1.

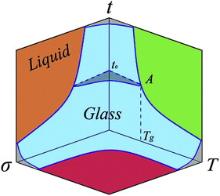
The diagrams involved in temperature and stress to describe the jamming and glass transition in different glasses are summarized^{[12], [13] and [35]}. Based on previous and our above results, we propose a speculative 3D glass transition diagram involved in observation time t (equivalent to ${\dot{γ}}^{- 1}$ ), T and stress σ. The interdependence of t, T and σ allows to plot the schematic 3D diagram for MGs as shown in Fig. 4. We use the curve forms of Fig. 4 to determine the phase boundaries. And we note that the values of the coefficient and shape of the glass transition surface may be different for details of specific glass systems^{[35] and [36]}. The glass region, near the origin, is enclosed by the depicted surface. According to the diagram, glass transition can be realized either by T, or by external stress or by changing observation time scale. We draw a horizontal cross-section through point t₀, which represents the usual experimental observation time scale (100 s) of glass transition ^[37], and the temperature corresponding to point A is the usual T_g. In the case of no applied stress, in the limit of T/ T_g << 1, the glass we see will flow if the observation time is long enough (or the strain rate is slow enough), which has been confirmed by experiments^{[16], [17] and [18]} and can interpret our observations in Sr-based MGs. By contrast, the liquid is solid glass-like as well when the observation time is infinitely short (equivalent to extremely large strain rate). Actually, in the supercooled liquid region, it is found that an increase in strain rate can lead to a transition from homogeneous flow to in homogeneous deformation, and makes the liquids behave solid like^{[38], [39], [40], [41], [42], [43], [44] and [45]}. Accordingly, the time, stress and temperature play the similar roles in glass transition, and the three parameters at each corner are divergent. The divergence in time axis reflects that in a sufficiently short time scale any viscous liquid behaves like a solid glass and a solid glass can be viewed as viscous liquid when the time scale is extended to infinite. The diagram helps to rationalize and unify the description of apparently diverse transitions from liquid-like to solid-like behaviors by means of glass transition in MGs. For practical applications, the diagram provides guidance in the parameters control to achieve a desired behavior and to search new glasses.

	Figure Option View Download New Window
	Fig. 4. Schematic 3D glass transition diagram involved in observation time t, temperature T, and stress σ for MGs. Data from the strain rate induced glass transition in SrCaYbMg(Li)Zn(Cu) MGs are used to construct the phase diagram. This diagram is a compendium of various MG systems. The glass region, near the origin, is enclosed by the depicted concave surfaces.

4. Conclusion

A glass to liquid-like homogeneous flow translation at RT occurs in Sr-based MGs when the strain rate reaches a critical value, which indicates that the action time of strain which is equivalent to observation time, like temperature and stress, is another intrinsic parameter to understand the glass transition. A 3D diagram involved in the observation time, stress and temperature is established to describe the glass transition in MGs. The temperature, observation time, and stress are equivalent control parameters, and the change of any of them has equivalent role in glass transition. The glass transition is the interplay between thermal energy, applied stress and action time scale. The work might be helpful for understanding the nature of the glass transition and for providing a unifying link between the glass transition and jamming.

References

Acknowledgment

This work was supported by the National Natural Science Foundation of China (No. 51271195).

The authors have declared that no competing interests exist.

Reference

View Option

1.	R. ZallenWiley-Interscience Publication (1983) [Cited within: 1]
2.	M. Q. Tang, H. F. Zhang, Z. W. Zhu, H. M. Fu, A. M. Wang, H. Li, Z. Q. Hu, J. Mater. Sci. Technol. , 26 (2010), pp. 481–486 [Cited within: 1] [JCR: 1.198] [CJCR: 0.293]
3.	H. H. Yan, Y. Hu, Z. Yan, X. Zheng, Y. Li, J. Mater. Sci. Technol. , 28 (2012), pp. 756–760 [Cited within: 1] [JCR: 1.198] [CJCR: 0.293]
4.	Q. He, J. Xu, J. Mater. Sci. Technol. , 28 (2012), pp. 1109–1122 [Cited within: 1] [JCR: 1.198] [CJCR: 0.293]
5.	W. H. Wang, Adv. Mater. , 21 (2009), pp. 4524–4544 [Cited within: 1] [JCR: 14.829]
6.	W. H. Wang, Prog. Mater. Sci. , 52 (2007), pp. 540–596 [Cited within: 1] [JCR: 23.194]
7.	P. N. Pusey, W. van Megen, Phys. Rev. Lett. , 59 (1987), pp. 2083–2086 [Cited within: 1] [JCR: 7.943]
8.	C. A. Angell, L. V. Woodcock, Adv. Chem. Phys. , 48 (1981), pp. 397–401 [Cited within: 1] [JCR: 5.25]
9.	E. Leutheusser, Phys. Rev. A, 29 (1984), pp. 2765–2770 [Cited within: 2] [JCR: 3.042]
10.	W. H. Wang, J. Appl. Phys. , 110 (2011), p. 053521 [Cited within: 1] [JCR: 0.71]
11.	B. Yang, C. T. Liu, T. G. Nieh, M. L. Morrison, P. K. Liaw, R. A. Buchanan, J. Mater. Res. , 21 (2006), pp. 915–919 [Cited within: 1] [JCR: 0.691]
12.	P. F. Guan, M. W. Chen, T. Egami, Phys. Rev. Lett. , 104 (2010), p. 205701 [Cited within: 3] [JCR: 7.943]
13.	A. J. Liu, S. R. Nagel, Nature, 396 (1998), pp. 21–22 [Cited within: 2] [JCR: 38.597]
14.	N. B. Olsen, T. Christensen, J. C. Dyre, Phys. Rev. Lett. , 86 (2001), pp. 1271–1274 [Cited within: 1] [JCR: 7.943]
15.	J. Lu, G. Ravichand ran, W. L. Johnson, Acta Mater. , 51 (2003), pp. 3429–3443 [Cited within: 3] [JCR: 3.941]
16.	K. W. Park, C. M. Lee, M. Wakeda, Y. Shibutani, M. L. Falk, J. C. Lee, Acta Mater. , 56 (2008), pp. 5440–5450 [Cited within: 2] [JCR: 3.941]
17.	H. B. Ke, P. Wen, H. L. Peng, W. H. Wang, A. L. Greer, Scripta Mater. , 64 (2011), pp. 966–969 [Cited within: 2] [JCR: 2.821]
18.	K. Zhao, X. X. Xia, H. Y. Bai, W. H. Wang, Appl. Phys. Lett. , 98 (2011), p. 141913 [Cited within: 3] [JCR: 3.794]
19.	B. Zhang, D. Q. Zhao, M. X. Pan, W. H. Wang, A. L. Greer, Phys. Rev. Lett. , 94 (2005), p. 205502 [Cited within: 1] [JCR: 7.943]
20.	H. B. Yu, X. Shen, Z. Wang, L. Gu, W. H. Wang, H. Y. Bai, Phys. Rev. Lett. , 108 (2012), p. 015504 [Cited within: 1] [JCR: 7.943]
21.	Q. Luo, W. H. Wang, J. Non-Cryst. Solids, 355 (2009), pp. 759–775 [Cited within: 1] [JCR: 1.597]
22.	X. Q. Gao, K. Zhao, H. B. Ke, D. W. Ding, W. H. Wang, H. Y. Bai, J. Non-Cryst. Solids, 357 (2011), pp. 3557–3560 [Cited within: 2] [JCR: 1.597]
23.	W. L. Johnson, K. Samwer, Phys. Rev. Lett. , 95 (2005), p. 195501 [Cited within: 1] [JCR: 7.943]
24.	H. B. Yu, W. H. Wang, H. Y. Bai, Y. Wu, M. W. Chen, Phys. Rev. B, 81 (2010), p. 220201 [Cited within: 2]
25.	Z. F. Zhang, F. Wu, G. He, J. Eckert, J. Mater. Sci. Technol. , 23 (2007), pp. 747–767 [Cited within: 3] [JCR: 1.198] [CJCR: 0.293]
26.	A. S. Argon, Acta Metall. , 27 (1979), pp. 47–53 [Cited within: 2] [JCR: 0.612] [CJCR: 0.835]
27.	Y. Kawamura, T. Shibata, A. Inoue, T. Masumoto, Mater. Trans. JIM, 40 (1999), pp. 336–342 [Cited within: 1]
28.	F. A. McClintock, S. A. Argon, Addison-Wesley, Reading, MA (1966), p. 273 [Cited within: 1]
29.	L. M. Martinez, C. A. Angell, Nature, 410 (2011), pp. 663–666 [Cited within: 1] [JCR: 38.597]
30.	M. L. Falk, J. S. Langer, Annu. Rev. Condens. Matter Phys. , 2 (2011), pp. 353–373 [Cited within: 1]
31.	M. Reiner, Phys. Today, 17 (1964), pp. 62–63 [Cited within: 2] [JCR: 6.762]
32.	J. C. Dyre, Rev. Mod. Phys. , 78 (2006), pp. 953–972 [Cited within: 3] [JCR: 44.982]
33.	F. Spaepen, Acta Metall. , 25 (1977), pp. 407–415 [Cited within: 3] [JCR: 0.612] [CJCR: 0.835]
34.	M. Bletry, P. Guyot, J. J. Bland in, J. L. Soubeyroux, Acta Mater. , 54 (2006), pp. 1257–1263 [Cited within: 2] [JCR: 3.941]
35.	V. Trappe, V. Prasad, L. Cipelletti, P. N. Segre, D. A. Weitz, Nature, 411 (2001), pp. 772–775 [Cited within: 2] [JCR: 38.597]
36.	Z. Zhang, N. Xu, D. T. N. Chen, P. Yunker, A. M. Alsayed, K. B. Aptowicz, P. Habdas, A. J. Liu, S. R. Nagel, A. G. Yodh, Nature, 459 (2009), pp. 230–233 [Cited within: 1] [JCR: 38.597]
37.	P. G. Debenedetti, F. H. Stillinger, Nature, 410 (2001), pp. 259–263 [Cited within: 1] [JCR: 38.597]
38.	W. L. Johnson, J. Lu, M. D. Demetriou, Intermetallics, 10 (2002), pp. 1039–1046 [Cited within: 1] [JCR: 1.857]
39.	X. L. Fu, Y. Li, C. A. Schuh, J. Mater. Res. , 22 (2007), pp. 1564–1569 [Cited within: 1] [JCR: 0.691]
40.	W. H. Wang, Z. X. Bao, C. X. Liu, D. Q. Zhao, J. Eckert, Phys. Rev. B, 61 (2000), pp. 3166–3169 [Cited within: 1]
41.	Z. Wang, P. Wen, L. S. Huo, H. Y. Bai, W. H. Wang, Appl. Phys. Lett. , 101 (2012), p. 121906 [Cited within: 1] [JCR: 3.794]
42.	W. Jiao, P. Wen, H. L. Peng, H. Y. Bai, B. A. Sun, W. H. Wang, Appl. Phys. Lett. , 102 (2013), p. 101903 [Cited within: 1] [JCR: 3.794]
43.	W. H. Wang, Prog. Mater. Sci. , 57 (2012), pp. 487–656 [Cited within: 1] [JCR: 23.194]
44.	W. H. Wang, J. Appl. Phys. , 99 (2006), p. 093506 [Cited within: 1] [JCR: 0.71]
45.	J. Q. Wang, W. H. Wang, Y. H. Liu, H. Y. Bai, Phys. Rev. B, 83 (2011), p. 012201 [Cited within: 1]

1983

0.0

... IntroductionMetallic glasses (MGs) with atomic randomly packing structure, excellent glass-forming ability and wide supercooled liquid temperature region are model system for studying the fundamental issues in glass field^{[1], [2], [3], [4], [5] and [6]} ...

2010

1.198

0.293

M. Q.

Tang

, H. F.

Zhang

, Z. W.

Zhu

, H. M.

, A. M.

Wang

, H.

, Z. Q.

, J. Mater. Sci. Technol. , 26 (2010), pp. 481–486

Low-cost TiZr-base bulk metallic glasses (BMGs) (Ti 36.1 Zr 33.2 Ni 5.8 Be 24.9 ) 100- x Cu x ( x =5, 7 and 9) with a maximum size of over 50 mm in diameter were developed by optimizing the alloy composition. The idea is initiated by selecting a particular microstructure comprising primary β-Ti dendrite and amorphous phase. Afterwards, based on this composition of amorphous phase, a class of TiZr-base bulk metallic glasses was designed step by step to reach the optimum composition range. The glass transition temperature ( T g ), initial crystallization temperature ( T x ) and width of supercooled region (Δ T ) of (Ti 36.1 Zr 33.2 Ni 5.8 Be 24.9 ) 91 Cu 9 BMG are 611, 655 and 44 K, respectively. The (Ti 36.1 Zr 33.2 Ni 5.8 Be 24.9 ) 91 Cu 9 BMG exhibits low density of 5.541 g·cm -3 and high compressive fracture strength of 1800 MPa, which promises the potential application as structural materials.

Shenyang National Laboratory for Materials Science, Institute of Metal Research, Chinese Academy of Sciences, 72 Wenhua Road, Shenyang 110016, China

2012

1.198

0.293

H. H.

Yan

, Y.

, Z.

Yan

, X.

Zheng

, Y.

, J. Mater. Sci. Technol. , 28 (2012), pp. 756–760

Zr 50 Cu 18 Ni 17 Al 10 Ti 5 bulk metallic glass has been rolled at room temperature up to 95% in thickness reduction, and the dependence of microstructure on the strain was investigated. With increasing thickness reduction, the full width at half maximum (FWHM) and crystallization enthalpy decrease gradually till 80%, and then increase evidently at 95%. It is revealed that the reversible transition between the ordered and disordered atomic configurations was found in the metallic glass as the deformation proceeds, which is further verified by the high-resolution transmission electron microscopy images. The final microstructure in metallic glass during cold-rolling is the net result of two competing processes between shear-induced disordering and diffusion controlled reordering.

School of Materials Science and Engineering, Taiyuan University of Science and Technology, Taiyuan 030024, China

在室温条件下对Zr50Cu18Ni17Al10Ti5块体金属玻璃进行了轧制变形，最大变形量为95%，研究了变形量与微观结构之间的关系。当变形量小于80%时，半高宽（FWHM）和晶化焓随着变形量的增加逐渐减小；当变形量超过80%，直至95%，FWHM和晶化焓又显著增加。结果表明，随着变形量的增加，该金属玻璃的原子结构发生了有序-无序的可逆转变，这一现象得到了高分辨透射电镜照片的进一步证实。金属玻璃在冷轧过程中的最终结构是剪切导致无序和扩散导致有序的两个过程竞争的结果。

2012

1.198

0.293

, J.

, J. Mater. Sci. Technol. , 28 (2012), pp. 1109–1122

We defined the plastic deformability under constrained loading conditions as malleability for bulk metallic glass (BMG) materials. Quaternary Zr-Ti-Cu-Al alloys in the Zr-rich composition range are selected to investigate the compositional dependence of malleability assessed by bending testing and glass transition temperature ( T g ). As indicated, increasing the Al or Cu concentration in the alloys leads to the rise of Tg. The Zr 61 Ti 2 Cu 25 Al 12 (ZT1) and Zr 61.6 Ti 4.4 Cu 24 Al 10 (ZT3) alloys exhibit an optimal combination of lower T g and higher glass-forming ability. The malleable BMGs such as ZT1 manifests two characters during deformation, the stable propagation of a single shear band indicated by large shear offsets and easy proliferation of shear bands. With increasing the T g of BMG, the yield strength σ y , Young0s modulus and shear modulus simultaneously increase as well, while the Poisson's ratio decreases. The σ y of ZT1 BMG is about 1680 MPa in compression and 1600 MPa in tension. In tensile loading, no any visible plasticity appears even when the strain rate increases up to the order of magnitude of 10 -1 s -1 . In consistent with the T g , malleability of Zr-Ti-Cu-Al BMGs manifests significant compositional dependence. The malleable BMG is associated with lower T g , as well as lower shear modulus or higher Poisson's ratio, which can be understood on the basis of the correlation of T g with shear energy barrier in metallic glass. Thus, the calorimetric T g can be used as an indicator to screen malleable BMG-forming composition, with advantage of experimental accessibility.

Shenyang National Laboratory for Materials Science, Institute of Metal Research, Chinese Academy of Sciences, Shenyang 110016, China

2009

14.829

0.0

2007

23.194

0.0

W. H.

Wang

, Prog. Mater. Sci. , 52 (2007), pp. 540–596

Abstract Bulk metallic glasses (BMGs) are of current interest worldwide in materials science and engineering because of their unique properties. Exploring BMGs materials becomes one of the hottest topics in the materials science field. To date, there is very active worldwide development of new BMGs, and extensive efforts have been carried out to understand and improve the glass-forming ability of metallic materials supported by large government and industry programs in North America, Asia, and Europe. Minor addition or microalloying technique, which has been widely used in other metallurgical fields, plays effective and important roles in formation, crystallization, thermal stability and property improvement of BMGs. This simple approach provides a powerful tool for the BMG-forming alloys development and design. In this paper, we present a comprehensive review of the history and the recent developments of this technique in the field of BMGs. The roles of the minor addition in the formation and the properties of the BMGs and the BMG-based composites will be discussed and summarized within the framework of thermodynamics, kinetics and microstructure. The empirical criteria, or the principles and guidelines for the applications of the technique in BMG field are outlined.

1987

7.943

0.0

... Generally, it is recognized that the glass transitions between supercooled liquid and glassy states in metallic glasses (MGs) are induced by thermalization or by applied stress^{[7], [8], [9], [10], [11], [12] and [13]} ...

1981

5.25

0.0

1984

3.042

0.0

... In fact, the glass transition is observation time dependent^[9] ...

2011

0.71

0.0

2006

0.691

0.0

2010

7.943

0.0

... ^[12] quantified the intimate coupling of temperature and shear stress in glass transition ...

... The diagrams involved in temperature and stress to describe the jamming and glass transition in different glasses are summarized^{[12], [13] and [35]} ...

1998

38.597

0.0

... The diagrams involved in temperature and stress to describe the jamming and glass transition in different glasses are summarized^{[12], [13] and [35]} ...

2001

7.943

0.0

... For polymer glasses, their responses to stress can be observed both within a short time at high temperature and a sufficient long time at low temperatures, which is time-temperature superposition principle^[14] ...

2003

3.941

0.0

, G.

Ravichand ran

, W. L.

Johnson

, Acta Mater. , 51 (2003), pp. 3429–3443

Abstract The stress-strain relations for the Zr 41.2 Ti 13.8 Cu 12.5 Ni 10 Be 22.5 bulk metallic glass (Vitreloy 1) over a broad range of temperatures (room temperature to its supercooled liquid region) and strain rates (10 −5 to 10 3 s −1 ) were established in uniaxial compression using both quasi-static and dynamic Kolsky (split Hopkinson) pressure bar loading systems. Relaxation and jump in strain rate experiments were conducted to further understand the time dependent behavior of Vitreloy 1. The material exhibited superplastic flow above its glass transition temperature (623 K) and strain rates of up to 1 s −1 . The viscosity in the homogeneous deformation regime was found to decrease dramatically with increasing strain rate. A fictive stress model was used to describe the basic deformation features of Vitreloy 1 under constant strain-rate loading as well as multiple strain-rate loading at high temperatures.

... This is because the MGs normally have high flow energy barrier below glass transition temperature (T_g), and the homogeneous deformation of MGs generally is only observed at high T or in inaccessible long time scale under stress at low T^{[15] and [16]} ...

... for Zr-based MGs, the superplastic flow occurs above 600 K ^[15]) ...

... The results clearly illustrate the similar roles of γ˙ and T in the homogeneous flow ^[15] ...

2008

3.941

0.0

K. W.

Park

, C. M.

Lee

, M.

Wakeda

, Y.

Shibutani

, M. L.

Falk

, J. C.

Lee

, Acta Mater. , 56 (2008), pp. 5440–5450

Abstract This study demonstrates that elastostatic compression imposed on amorphous alloys at room temperature induces irreversible structural disordering. The rate of disordering depends on the atomic packing density as determined by the fraction of the material in short-range ordered (SRO) atomic environments. The structural disordering, measured experimentally by differential scanning calorimetry, in turn alters the mechanical properties of the material. A combination of experiments and molecular dynamics simulations are used to explore fundamental issues related to shear-induced disordering during elastostatic compression.

... In the case of no applied stress, in the limit of T/T_g [16], [17] and [18] and can interpret our observations in Sr-based MGs ...

2011

2.821

0.0

H. B.

, P.

Wen

, H. L.

Peng

, W. H.

Wang

, A. L.

Greer

, Scripta Mater. , 64 (2011), pp. 966–969

Room-temperature uniaxial compression of Zr 46.75 Ti 8.25 Cu 7.5 Ni 10 Be 27.5 bulk metallic glass at 80% of the yield stress leads to homogeneous viscous flow. The flow in this apparently elastic regime reveals large increases in volume associated with local shearing events in the glass. The extent of this dilatation is masked in more usual tests by significant relaxation of the glass structure during and after shear. The dilatation in deformed metallic glasses can no longer be attributed only to free-volume generation at shear bands. Research highlights ? We study compressive loading of a metallic glass below the yield stress. ? The directly measured density decrease verifies earlier indirect inferences. ? There is a dilatation of roughly one atomic volume per atom involved in shear. ? Volume changes cannot now be attributed only to shear bands. ? The relative changes of shear and bulk moduli are not as expected.

... 0 × 10^-4^[17] ...

... In the case of no applied stress, in the limit of T/T_g [16], [17] and [18] and can interpret our observations in Sr-based MGs ...

2011

3.794

0.0

... Recently, some MGs such as Ce-, La- and Sr-based with low T_g have been developed ^{[18], [19], [20] and [21]} ...

... Remarkable liquid-like homogeneous flow near room temperature and under relatively high strain rates can be realized in the Sr-based glasses due to their very low flow activation energy ^{[18] and [22]} ...

... In the case of no applied stress, in the limit of T/T_g [16], [17] and [18] and can interpret our observations in Sr-based MGs ...

2005

7.943

0.0

... Recently, some MGs such as Ce-, La- and Sr-based with low T_g have been developed ^{[18], [19], [20] and [21]} ...

2012

7.943

0.0

... Recently, some MGs such as Ce-, La- and Sr-based with low T_g have been developed ^{[18], [19], [20] and [21]} ...

2009

1.597

0.0

... Recently, some MGs such as Ce-, La- and Sr-based with low T_g have been developed ^{[18], [19], [20] and [21]} ...

2011

1.597

0.0

... 45)₂₀Zn₂₀ MGs of 2 mm in diameter were prepared by copper mold casting method^[22] ...

2005

7.943

0.0

... According to the shear cooperative model ^[23], the barrier energy of plastic flow units W_STZ (also termed as shear transformation zones (STZs)) in MGs can be estimated by ^[24]W_STZ∝0 ...

2010

0.0

... According to the shear cooperative model ^[23], the barrier energy of plastic flow units W_STZ (also termed as shear transformation zones (STZs)) in MGs can be estimated by ^[24]W_STZ∝0 ...

... Clearly, these MGs have much lower activation energy of flow units compared with that of conventional MGs ^[24] and the activation of flow units is then much easier ...

2007

1.198

0.293

Z. F.

Zhang

, F.

, G.

, J.

Eckert

, J. Mater. Sci. Technol. , 23 (2007), pp. 747–767

The deformation, damage, fracture, plasticity and melting phenomenon induced by shear fracture were investigated and summarized for Zr-, Cu-, Ti- and Mg-based bulk metallic glasses (BMGs) and their composites. The shear fracture angles of these BMG materials often display obvious differences under compression and tension, and follow either the Mohr-Coulomb criterion or the unified tensile fracture criterion. The compressive plasticity of the composites is always higher than the tensile plasticity, leading to a significant inconsistency. The enhanced plasticity of BMG composites containing ductile dendrites compared to monolithic glasses strongly depends on the details of the microstructure of the composites. A deformation and damage mechanism of pseudo-plasticity, related to local cracking, is proposed to explain the inconsistency of plastic deformation under tension and compression. Besides, significant melting on the shear fracture surfaces was observed. It is suggested that melting is a common phenomenon in these materials with high strength and high elastic energy, as it is typical for BMGs and their composites failing under shear fracture. The melting mechanism can be explained by a combined effect of a significant temperature rise in the shear bands and the instantaneous release of the large amount of elastic energy stored in the material.

Shenyang National Laboratory for Materials Science, Institute of Metal Research, Chinese Academy of Sciences, Shenyang 110016, China...

... The fracture approaches the ideal brittle behavior^[25], which indicates that at RT the MG is in glassy state ...

... accumulation of free volume) accompanied by softening ^{[25] and [26]} ...

... At relatively low strain rates, the rate of free volume annihilation gradually comes to match that of production, and a steady state condition is eventually achieved ^{[25] and [26]} ...

1979

0.612

0.835

... accumulation of free volume) accompanied by softening ^{[25] and [26]} ...

... At relatively low strain rates, the rate of free volume annihilation gradually comes to match that of production, and a steady state condition is eventually achieved ^{[25] and [26]} ...

1999

0.0

... The relationship of apparent viscosity η of homogeneous flow, γ˙ and the flow stress σ _flow can be expressed as ^{[27] and [28]}: γ˙=σflow/3η ...

0.0

... The relationship of apparent viscosity η of homogeneous flow, γ˙ and the flow stress σ _flow can be expressed as ^{[27] and [28]}: γ˙=σflow/3η ...

2011

38.597

0.0

... The dynamical definition of glass transition is that the viscosity of the supercooled liquid reaches ∼10¹³ Pa s ^{[29] and [30]} ...

2011

0.0

... The dynamical definition of glass transition is that the viscosity of the supercooled liquid reaches ∼10¹³ Pa s ^{[29] and [30]} ...

1964

6.762

0.0

... The Maxwell relaxation time τ provides a key to understanding the glass transition ^{[31] and [32]} ...

... The glass transition is observation time dependent, and difference between glasses and fluid liquid can be defined by a nondimensional number of the so-called Deborah number ^{[31] and [32]}: D = t_r/t_o, where t_r is the time of relaxation, and t_o is the time of observation ...

2006

44.982

0.0

... The Maxwell relaxation time τ provides a key to understanding the glass transition ^{[31] and [32]} ...

... A viscous liquid can be viewed as solid which flows in enough short time scale, and a glass can be regarded as viscous liquid in enough large time scale ^[32] ...

1977

0.612

0.835

... According to the general steady state flow theory ^[33], the relation between the σ and γ˙ is given by ^{[34] and [33]}, ...

... At a given temperature of RT, the ν_D,Δ G^mand Vare constant, and the relation between the σ_maxand γ˙is ^{[33] and [34]}, ...

2006

3.941

0.0

Bletry

, P.

Guyot

, J. J.

Bland in

, J. L.

Soubeyroux

, Acta Mater. , 54 (2006), pp. 1257–1263

Abstract The homogeneous deformation of a zirconium-based bulk metallic glass is investigated in the glass transition region. Compression tests at different temperatures and strain rates have been conducted. The mechanical behavior is analyzed in the framework of the free volume model, taking into account the dependence of the flow defect concentration on deformation. The activation volume is evaluated and allows one to gather the viscosity data (for the different strain rates and temperatures) on a unique master curve. It is also shown that, due to the relation between flow defect concentration and free volume, it is not possible to deduce the equilibrium flow defect concentration directly from mechanical measurements. However, if this parameter is arbitrarily chosen, mechanical measurements give access to the other parameters of the model, these parameters for the alloy under investigation being of the same order of magnitude as those for other metallic glasses.

... According to the general steady state flow theory ^[33], the relation between the σ and γ˙ is given by ^{[34] and [33]}, ...

... At a given temperature of RT, the ν_D,Δ G^mand Vare constant, and the relation between the σ_maxand γ˙is ^{[33] and [34]}, ...

2001

38.597

0.0

... The diagrams involved in temperature and stress to describe the jamming and glass transition in different glasses are summarized^{[12], [13] and [35]} ...

... And we note that the values of the coefficient and shape of the glass transition surface may be different for details of specific glass systems ^{[35] and [36]} ...

2009

38.597

0.0

... And we note that the values of the coefficient and shape of the glass transition surface may be different for details of specific glass systems ^{[35] and [36]} ...

2001

38.597

0.0

... We draw a horizontal cross-section through point t₀, which represents the usual experimental observation time scale (100 s) of glass transition ^[37], and the temperature corresponding to point A is the usual T_g ...

2002

1.857

0.0

... Actually, in the supercooled liquid region, it is found that an increase in strain rate can lead to a transition from homogeneous flow to in homogeneous deformation, and makes the liquids behave solid like ^{[38], [39], [40], [41], [42], [43], [44] and [45]} ...

2007

0.691

0.0

2000

0.0

2012

3.794

0.0

2013

3.794

0.0

2012

23.194

0.0

2006

0.71

0.0

2011

0.0