1. Introduction
The corrosion is the result of chemical, electrochemical or physical interactions between materials and their surrounding environments [1]. It not only threatens the construction safeties [2], but also leads to huge economic losses. According to surveys and expert experiences, the annual economic losses caused by corrosion reaches about 4 trillion dollars in the worldwide [3]. However, the losses could be reduced by 25 %-30 % with the help of effective corrosion models and scientific management [4]. Furthermore, the model can also be used to the potential unknown knowledge mining within the corrosion data [5,6]. Therefore, the study of corrosion prediction model has an important research significance in the material corrosion engineering.
Recently, corrosion researchers use machine-learning algorithms such as artificial neural networks (abbreviated as ANN) [[5], [6], [7], [8], [9], [10], [11]], support vector machines (abbreviated as SVM) [[12], [13], [14], [15]], power and power-linear function [16], hidden markov model (abbreviated as HMM) [[17], [18], [19], [20], [21]], etc. to implement the modeling [[6], [7], [8],10,[6], [7], [8], [9], [10], [11], [12], [13], [14], [15], [16],18], forecasting [5,9,12,16,17,19,20] and da ta mining [5,7,8,21] of the corrosion data. However, for most of the above works, the corrosion samples are obtained by indoor corrosion experiments or corrosion current experiments with just one single material [5,7,8,11,12,14,15] or one single input variable [16,17,21]. The corrosion predictions of various materials in a variety of outdoor environmental conditions still pose challenges to those commonly used models.
Nowadays, a new machine-learning algorithm called random forests (abbreviated as RF) [22] has attracted the attention of scholars. RF is a branch of ensemble methods, which has the advantages of easy-implementation, anti-overfitting, excellent-performance, robustness, interpretability, etc [23,24]. Additionally, RF can be used to infer each variable importance and extract the key variables [25,26]. Therefore, RF are widely used in the fields of image recognition [27], geography [28], economics [29], manufacture [30], agriculture [31], etc. In the corrosion field, researchers use RF to implement the corrosion current classification [32,33], corrosion severity classification [34] and crack growth rate analysis [35]. As for outdoor atmospheric corrosion rate modelling, the previous results show that RF can obtain better results than general methods like ANN, SVR and linear-regression [36]. The above studies illustrate that RF is an appropriate approach of the corrosion datasets modelling.
To further improve the performances of RF, researchers propose other models such as the weighted combination of base tree models [49,50], the deep-structure RF model [38], etc. The weighted combination model assigns different weighted values to different base tree models to weaken the influences of low accuracy tree models. The deep structure model enhances the representation ability by change the way of model structures. However, the above improved methods only solve classification problem, neither regression nor prediction. In this paper, we propose a new RF model, called Densely Connected Cascade Forest-Weighted K Nearest Neighbors (abbreviated as DCCF-WKNNs). It is a layer-by-layer representation algorithm, and each layer consists of several RF-WKNNs, i.e. a weighted assigning method of RF model, to implement the corrosion rate prediction (regression) and data-mining. For verifying the performance of the proposed method, we use 409 low-alloy steels corrosion samples under outdoor atmospheric condition as experimental datasets [36]. The experimental results show that the proposed method had a better performance than ANN, SVR and RF model. Additionally, the paper uses the proposed method to forecast the trend of corrosion rate when one input variable changes. It can find out a threshold of each variable, which acts as an importance factor of assisting material corrosion. For example, the results show that the critical relative humidity of the outdoor sites is 65 %.
The organization of the paper is as follows. The collected corrosion samples are described in Section 2. In Section 3, the random forests-weighted K-nearest neighbors (abbreviated as RF-WKNNs) is discussed, and then the structure of multiple-layer deep model is illustrated. The prediction and data mining results based on the proposed methods are shown in Section 4. The summary of the data analysis and conclusions are in Section 5.
2. Experimental
The paper selects the outdoor atmospheric corrosion samples of low-alloy steels (abbreviated as LAS) as experimental datasets. LAS, itself, has a good corrosion resistance due to the addition of alloying elements (Cu, P, Cr, Ni, etc.) [39,41]. The collected data is obtained from 6 different atmospheric test sites in China. For all the sites, there are 17 kinds of LAS being tested over 16 years. A total of 409 LAS corrosion samples are collected as experimental datasets. In the datasets, each sample has the following dimensions, e.g. material, environment, exposure time and corresponding corrosion rate.
(1)The difference between 17 LAS is represented by the composition of 8 chemical elements (Mn, S, P, Si, Cr, Cu, Ni, and Fe), and Table 1 shows the detailed element compositions of 17 LAS.
Table 1 Element compositions of 17 LAS in collected datasets.
| Alloy | Element Compositions (wt.%) | |||||||
|---|---|---|---|---|---|---|---|---|
| Mn | S | P | Si | Cr | Cu | Ni | Fe | |
| 06CuPCrNiMo | 0.40 | 0.023 | 0.050 | 0.17 | 0 | 0.17 | 0 | Balance |
| 09CuPCrNiA | 0.40 | 0.023 | 0.015 | 0.26 | 0.10 | 0.05 | 0.02 | Balance |
| 09CuPTiRe | 0.40 | 0.019 | 0.080 | 0.28 | 0 | 0.29 | 0 | Balance |
| 09MnNb(s) | 1.18 | 0.024 | 0.027 | 0.20 | 0.10 | 0.05 | 0.10 | Balance |
| 10CrCuSiV | 0.31 | 0.002 | 0.010 | 0.62 | 0.83 | 0.25 | 0.10 | Balance |
| 10CrMoAl | 0.45 | 0.002 | 0.012 | 0.35 | 0.98 | 0.09 | 0 | Balance |
| 14MnMoNbB | 1.53 | 0.010 | 0.022 | 0.34 | 0.10 | 0.05 | 0 | Balance |
| 15MnMoVN | 1.52 | 0.004 | 0.026 | 0.40 | 0.10 | 0.05 | 0 | Balance |
| 16Mn | 1.40 | 0.025 | 0.009 | 0.36 | 0.10 | 0.05 | 0 | Balance |
| 16MnQ | 1.37 | 0.023 | 0.030 | 0.30 | 0.10 | 0.07 | 0.05 | Balance |
| D36 | 1.40 | 0.018 | 0.022 | 0.39 | 0.05 | 0.05 | 0 | Balance |
| JN235(RE) | 0.52 | 0.025 | 0.030 | 0.30 | 0.10 | 0.07 | 0 | Balance |
| JN255 | 0.67 | 0.006 | 0.016 | 0.07 | 0.02 | 0.05 | 0.05 | Balance |
| JN255(RE) | 0.39 | 0.005 | 0.010 | 0.62 | 0.83 | 0.25 | 0.10 | Balance |
| JN345 | 0.39 | 0.005 | 0.110 | 0.05 | 0.90 | 0.40 | 0.65 | Balance |
| JN345(RE) | 0.36 | 0.011 | 0.089 | 0.28 | 0 | 0.29 | 0 | Balance |
| JY235(RE) | 0.27 | 0.010 | 0.089 | 0.28 | 0 | 0.29 | 0 | Balance |
(2)The atmospheric test sites cover the typical climate situations in China. In the paper, we select 6 environmental factors and they are average relative humidity, average temperature, rainfall, SO2 concentration, pH of rain, and chloride concentration. These factors are selected because of two main reasons. One reason is that many relevant works prove that these 6 factors have a critical impact on corrosion. For example, a critical relative humidity value can decide the corrosion phenomenon happens or not [40], and SO2, along with chloride could accelerate the corrosion rate while keeping other factors stable [41,42]. The other reason is that the consideration of the data-completeness has to ignore the missing data of other dimensions. The environmental factors information is shown in Table 2.
Table 2 Environmental factors and their statistical values.
| Factors | Average | Minimum | Maximum |
|---|---|---|---|
| Average Relative Humidity, RH (s%) | 75.09 | 56.17 | 87.71 |
| Average Temperature,T (℃) | 17.58 | 11.08 | 26.05 |
| Rainfall (mm/month) | 159.74 | 45.64 | 753.00 |
| SO2 concentration, SO2 (mg/cm3) | 0.09 | 0.02 | 0.30 |
| pH of rain (pH) | 6.14 | 5.11 | 6.97 |
| Chloride concentration, Cl- (mg/cm3) | 0.22 | 0 | 1.97 |
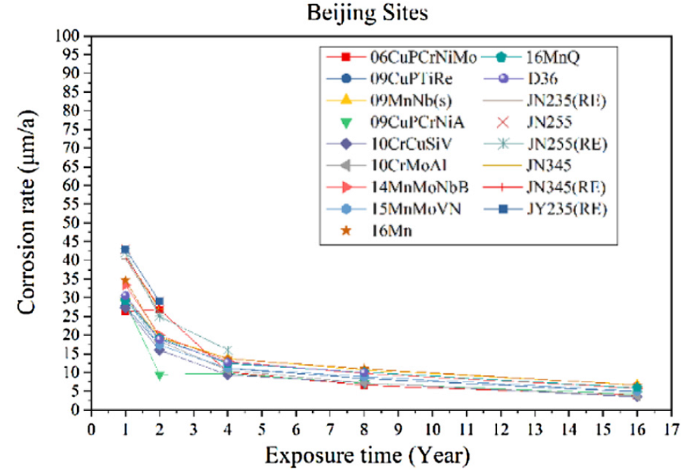
(3)For each steel, we take the 1 st, 2nd, 4th, 8th and 16th year as sampling time period and collect the corrosion rate at each period. Taking Beijing as an example, we visualize the corrosion rates of 17 LAS vs exposure time in Fig. 1.
Fig. 1.
Corrosion rates of LAS versus exposure time in Beijing.
As for modelling corrosion relationship, we take material components, environmental factors, exposure time as model input and take the corrosion rates as model output.
3. Methods
The framework of the proposed method is shown in this section. The method has two parts to combine with. The first part introduces the random forests-weighted k-nearest neighbors (abbreviated as RF-WKNNs) which is a modification of traditional RF model and can improve the generalization performance of RF for new samples. The second part gives the framework of proposed deep-structure methods based on RF-WKNNs and cForest [38], considering the advantages of RF-WKNNs and layer-by-layer representation of cForest. In addition, three evaluation criteria are adopted to evaluate the performance of the proposed model.
3.1. Random forests-weighted K-Nearest neighbors (RF-WKNNs)
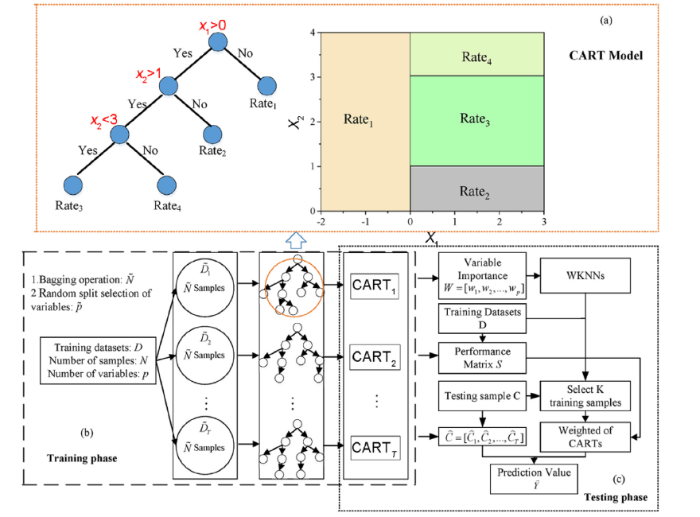
Random forests (RF) is an ensemble of multiple tree models. For a given sample, each tree can output a prediction value, and RF model outputs the aggregation of all the tree outputs, as the final prediction results. In general, the aggregate is just the average computation, resulting in the same weight on each tree. However, some tree models may fail in prediction due to the random selection samples or variables in training phase. Therefore, we expect to assign different weights for different tree models after training phase, and give the large weights for high accuracy trees and small weights for low accuracy trees, the weighted aggregate of all the trees can obtain a better performance than traditional RF model. Hence, we propose an improved method called random forest-weighted K nearest neighbors (RF-WKNNs) which can assign dynamic weights for different tree models. The framework of RF-WKNNs is shown in Fig. 2.
Fig. 2.
Fig. 2.
Framework of RF-WKNNs. (a) Example of CART model; (b) Training phase of RF-WKNNs; (c) Testing phase of RF-WKNNs.
According to Fig. 2, the whole process of RF-WKNNs includes two parts: training phase (a.k.a fitting phase) and testing phase (a.k.a generalization phase). The former phase is to learn the model parameters by training samples, the latter phase is used to evaluate the performance of the model.
As illustrated in Fig. 2, the training phase is to build T tree models of RF. In this paper, we use the classification and regression tree (abbreviated as CART) as the tree model. CART splits the parent node into two children nodes once. The example of a trained CART model structure is shown in Fig. 2(a). Assuming that the input is a two-dimension variable: X1 and X2. If X1≤0, then the prediction rate is Rate1; if X1>0 and X2≤1, then Rate2; if X1>0 and 1<X2<3, then Rate3; if X1>0 and X2≥3, then Rate4.
The detailed process of training and testing phase of RF-WKNNs will be shown in the next section.
3.1.1. Training phase
The training phase of RF-WKNNs is the same as that of RF model, which uses a training dataset to generate several trees with different model structures and parameters. To ensure the diversity of tree models, RF merges two important operations: bagging and random selection of variables.
From Fig. 2, the original training datasets is $D=\left\{ \left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right),\ldots ,\left( {{x}_{N}},{{y}_{N}} \right) \right\} $, ${{x}_{i}}=\left[ x_{i}^{1},x_{i}^{2},\ldots ,x_{i}^{p} \right] $. It contains N training samples, and each sample consists of p variables. Based on the datasets D, we perform the bagging and random selection of variables operation.
Firstly, the bagging (bootstrap aggregation) operation is used to construct sub-datasets for each tree model by randomly sampling with replacement from the original training datasets D. For example, there are N samples in D, and the selection probability of each sample is 1/N. In order to generate $\tilde{N} $(is equal to N generally) samples to train a CART model, we will randomly select one sample from D and repeat the selection with $\tilde{N} $ times. Then, there will be part of samples being selected with several times and part of samples not being selected ever. According to the statistical calculation, there are about 37 % of all the samples not being selected, and these samples are called out-of-bag (abbreviated as OOB) [23,32]. The OOB samples are just used to calculate the variable importance, and the specific algorithm refers to the work [32,36]. By bagging operation, the training samples are made different for each tree model, and the variance of the final ensemble model structure is reduced [37].
The second operation is the randomly selection of variables, i.e. only a random subset of all the p variables is considered at each node of the tree. This operation gives weak features a chance to be considered in the tree [38]. Based on the above two operations, we can obtain T different CART models with one single datasets D, as shown in Fig. 2(b).
3.1.2. Testing phase
In Fig. 2(c), for a given testing sample denoted by C, the testing phase of RF-WKNNs is to implement the weight combination of prediction values of all CARTs. The testing phase includes several steps as follows:
Step 1. Calculate the importance value of each input variable by the trained RF model [32,36], and obtain the importance of input variables $W=\left[ {{w}_{1}},{{w}_{2}},\ldots ,{{w}_{p}} \right],0<{{w}_{i}}<1,\underset{i-1}{\overset{p}{\mathop \sum }}\,{{w}_{i}}=1 $, where ${{w}_{i}} $ represent the importance of i-th variable.
Step 2. Compute the performance of each trained CART model on each training sample, and a performance matrix S is obtained:
where, Yn represents the real value of n-th training sample, and ${{\overset{}{\mathop{Y}}\,}_{nt}} $ represents the prediction value of t-th CART model on n-th training sample. There is a new parameter in Eq. (1), called threshold, which controls the sparse degree of the performance matrix S. When the threshold is set to be near to 1, most of elements in matrix S tends to be 1, and it means that almost every CART model can meet the requirement performance, leading to the weighted combination trivial. When the threshold is set to be near to 0, most of elements in S are tend to be 0, and it means that most of CART models can’t meet the performance requirement, leading to the weighted combination is too sparse to have a robust final model.
Step 3. Based on variables importance W, the WKNNs is constructed. Therefore, the similar equation between sample $A=\left[ {{a}_{1}},{{a}_{2}},\ldots ,{{a}_{p}} \right] $ and $B=\left[ {{b}_{1}},{{b}_{2}},\ldots ,{{b}_{p}} \right] $ is follows:
The smaller the weighted mean square error between A and B, the higher the similarity between samples.
Step 4. For a given testing sample C, calculate the similar value between C and each training samples. Then, select K nearest training samples.
Step 5. Based on the training samples and performance matrix S in Step 2, calculate the weighted value of CART models wc = $\left[ w_{1}^{c},w_{2}^{c},\ldots ,w_{T}^{c} \right] $. For example, assuming that the K in KNNs is 3, the selection of K-nearest training samples for new sample is Nos.3, 7 and 8. Then, $w_{i}^{C} $ =( ${{s}_{3i}}+{{s}_{7i}}+{{s}_{8i}} $)/3, i = 1, 2, …,T.
Step 6. Input C into all CART model, obtain the prediction value vector $\overset{}{\mathop{C}}\,=\left[ {{\overset{}{\mathop{C}}\,}_{1}},{{\overset{}{\mathop{C}}\,}_{2}},\ldots ,{{\overset{}{\mathop{C}}\,}_{T}} \right] $. These prediction values will be combined with weights and then the final prediction value ${{\overset{}{\mathop{Y}}\,}_{C}} $ is provided:
3.2. Densely connected cascade forests-WKNNs (DCCF-WKNNs)
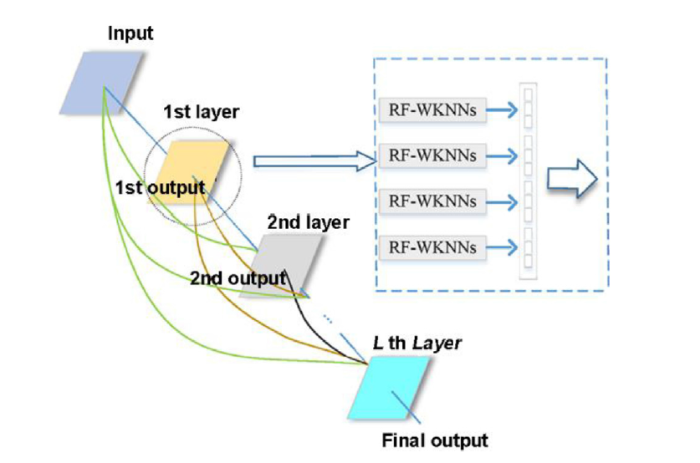
Recently, deep learning is applied and studied in many fields because of its superior performances. The learning process and structure in deep learning make itself applicable to solve the challenges which cannot be solved before. Among various deep-structure models, a kind of deep model called gcforest is proposed in 2017 [38]. It is based on RF modelling and representative learning to improve the capability of understanding audio and video information. Unlike most of deep learning structures, the gcforest can be used for the small sample dataset with just a few hyper-parameters to adjust. Based on the idea of gcforest, we propose a new deep-structure model called DCCF-WKNNs, which can be applied to the field of corrosion dataset. The framework of the proposed method is shown in Fig. 3.
Fig. 3.
Fig. 3.
Framework of proposed DCCF-WKNNs model.
As illustrated in Fig. 3, the DCCF-WKNNs is a layer-by-layer representation method. Each layer is composed of four RF-WKNNs model which is shown in Section 3.1, and each layer will transport the output to all the latter layers as the input variables.
In order to confirm the final layer of DCCF-WKNNs, we need to split a few samples from training samples as validation datasets and input the selected validation datasets into the RF-WKNNs model of the current layer. If the result is better than the result of the previous layer, it means that the performance of the current layer is better than the previous layer, and the training procedure continues to generate next layer. Otherwise, the performance of current layer is worse than the previous layer, and the training procedure is better to stop generation of the next layer.
3.3. Evaluation criteria
Three criteria are used to evaluate the training and testing results of model, which are as follows:
(1)Mean absolute percentage error (MAPE)
where N is the number of samples, ${{\overset{}{\mathop{y}}\,}_{n}} $ and ${{y}_{n}} $ represent the prediction and the true value of n-th sample. The smaller MAPE, the better prediction of the model.
(2)Root mean square error (RMSE):
The smaller RMSE, the better prediction of the models.
(3)Determination coefficients (R2):
where, $\bar{y}=\underset{n-1}{\overset{N}{\mathop \sum }}\,{{y}_{n}}/N $ is the mean of the true values of all samples. With R2 approaching to 1, the model capability becomes better.
4. Results and discussion
4.1. Determination of layer number
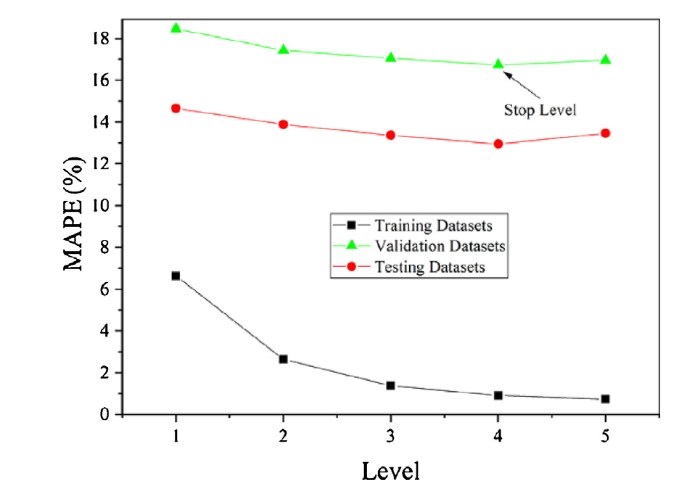
As mentioned above in Section 3.2, the proposed DCCF-WKNNs belongs to a kind of multi-layer representative model, and the number of layers needs to be determined by training datasets and validation datasets. Therefore, we randomly split the whole datasets into training, validation and testing with the proportion to be 4:1:2. We observe the MAPE of training, validation and test datasets and decide the number of layers. The main consideration is that when the model is deep enough, the layers cannot give more information to the subsequent layers but increase the complexity adversely. Therefore, A proper deep structure is preferred. Fig. 4 is the MAPE values with different layers on the collected corrosion datasets.
Fig. 4.
Fig. 4.
Choice of number of layers using MAPE.
From Fig. 4, we know that when 4-layer is fixed, the MAPE is satisfactory and reaches the lowest position for validation datasets. It shows 4-layer structure can have the best generalization performance for the datasets. Therefore, in our paper, we determine to establish a 4-layer DCCF-WKNNs model.
4.2. Comparison results of several methods
We compare the corrosion rate prediction results with several methods, such as ANN, SVR, traditional RF, RF-WKNNs and cForest [38]. For good performances of each algorithms, we set a series of hyper-parameters before modelling. The specific parameter values are as follows:
(1)For ANN algorithm, we set the architecture of model is: 15-100-1 (15 input variables, 100 hidden neurons, 1 output neuron). Furthermore, the transfer functions which reside in hidden and output layer are ReLu function. The stochastic gradient descent method is used to the parameter learning and tuning. The learning rate is set to 0.001, and model training stops when the iteration reaches 300 times.
(2)For SVR algorithm, we set the kernel function to be radial basis function (RBF), and the corresponding width is 1. The tolerance error is 300. According to the practical experiments, the smaller the values of width and tolerance error are, the poorer the training and testing results. While the values of width and tolerance error become large, the training error is low but the testing error is very large. The above values are decided by many experiments in our paper.
(3)For RF algorithm, we set the number of CART in RF to be 1000. The minimum sample number of leaves in CART is 3, which means that when the training samples in the node of CART is equal or less than 3, the split is stopped at this node and the node is treated as leaf node of CART.
(4)For RF-WKNNs algorithm, there are two additional parameters based on RF model. The first parameter is the threshold in Eq. (1), and when the parameter is set too small, most of elements in performance matrix S are 0, while when the value is too large, most of elements in S are 1. Both are not expected when making the model. Here, we set the value of threshold is 0.3, based on several experiments. The second parameter is the K of KNNs algorithm, and we set the K value to be 2.
(5)For cForest algorithm, it is the combination of several layers, and each layer contains several RF models. Based on the literature [38], we set the RF number in each layer to be 4, and the parameters in each RF have been mentioned above.
(6)For the proposed algorithm, it is the combination of cForest and RF-WKNNs. The values of threshold, K are equal to the RF-WKNNs mentioned above. The RF-WKNNs number in each layer, CART numbers in each RF-WKNNs, and the minimum samples number of leaves in CART are set as the same in the cForest model.
The following Table 3 shows the criteria results for those methods, including the fitting results using training dataset and generalization results using test dataset.
Table 3 Comparison of different methods for fitting and generalization.
| Methods | Fitting Results (Training samples) | Generalization Results (Testing samples) | ||||
|---|---|---|---|---|---|---|
| MAPE (%) | RMSE | R2 | MAPE (%) | RMSE | R2 | |
| ANN | 0.28 | 0.08 | 1.000 | 28.16 | 8.35 | 0.785 |
| SVR | 3.66 | 3.33 | 0.960 | 25.16 | 7.45 | 0.823 |
| RF | 6.02 | 2.32 | 0.980 | 16.21 | 5.46 | 0.908 |
| RF-WKNNs | 6.02 | 2.32 | 0.980 | 15.31 | 5.36 | 0.911 |
| cForest | 0.78 | 0.43 | 1.000 | 15.22 | 5.09 | 0.920 |
| DCGF-WKNNs | 0.89 | 0.44 | 1.000 | 12.95 | 4.95 | 0.924 |
From Table 3, we see that compared with traditional RF model, the proposed RF-WKNNs can obtain better performances in testing samples. It can be seen that the combination of weighted trees can improve the generalization ability of RF model. The cForest, the multiple-layer version of RF model, can achieve the sub-optimal results in testing samples. And the best generalization results are given by the proposed DCCF-WKNNs which adopts the advantages in both the RF-WKNNs and cForest.
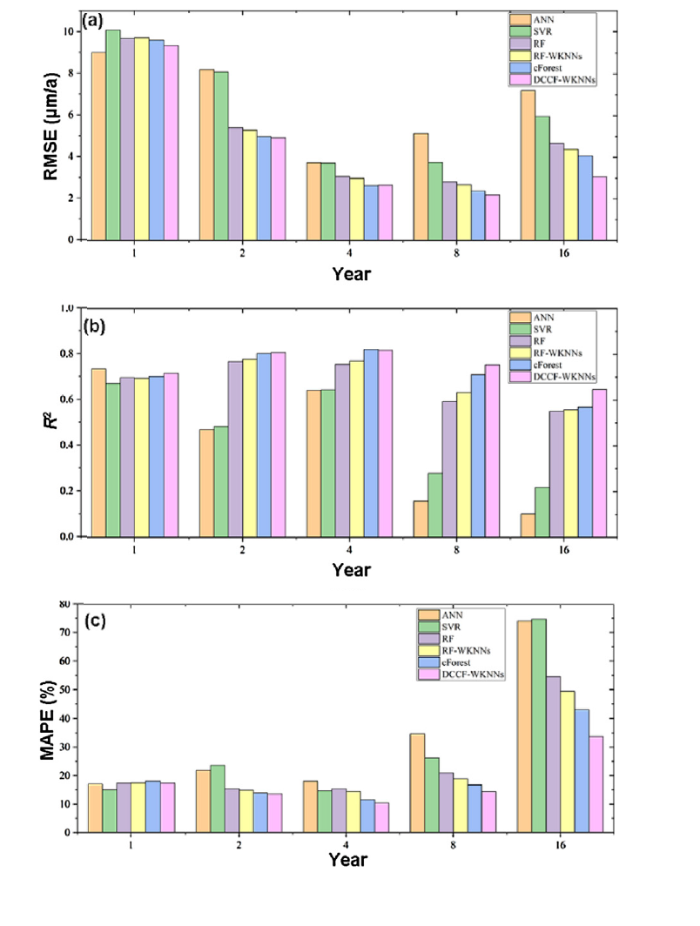
Furthermore, we respectively test the different stages of corrosion rate prediction, that is to split the data by the time dimension. As for datasets in this paper, in order to test the performance of 6 models in corrosion samples with 1-year exposure time, we use other samples as training samples to train the models, and the trained models are applied to forecast the corrosion rate of samples of which the exposure time is 1 year. In this way, we can give the models for each time period of corrosion situation based on 6 methods. Fig. 5 is the results.
Fig. 5.
Fig. 5.
Performances of different time periods of 6 methods: (a) RMSE results of 6 methods in sub-datasets with different exposure time; (b) R2 results of 6 methods in sub-datasets with different exposure time; (c) MAPE results of 6 methods in sub-datasets with different exposure time.
Fig. 5 shows the results of three evaluation criteria of 6 methods in each period. The Fig. 5(a) shows the RMSE which can be used to show the absolute error of real-value and predict-value. Fig. 5(b) shows the R2 criterion which can be used to show the fitting precision of model. Fig. 5(c) shows the MAPE criterion which is applied to demonstrate the relative error of real-value and predict-value. Among these three criteria, better performance of the model corresponds to smaller RMSE, MAPE value and larger R2 value, and vice versa. According to the analysis of three sub-graph of Fig. 5(a), we can infer that ANN has a slightly better results than the proposed DCCF-WKNNs in 1 st year, but has much worse results in other period time. RF-WKNNs almost always perform better than traditional RF model except for the 1 st year. The proposed DCCF-WKNNs almost keeps the best results along with time dimension, and the obvious superiority shows up with increasing time. It means DCCF-WKNNs model is able to model the data in a more sound way and give stable and confident results.
4.3. Corrosion knowledge mining results
In this part, the proposed model measures the quantitative effects of 6 environmental factors. The aim of measuring is to discover the thresholds by which the corrosion rate varies sharply. For example, different temperature ranges cause different corrosion degree and these facts often show up obvious step phenomena, in other words, there exist thresholds making corrosion rate change greatly. Traditional methods are hardly to find those thresholds. While using our proposed DCCF-WKNNs, it provides a way to find. DCCF-WKNNs fixes part of input variables and lets one input variable change within a certain range. Afterwards, we observe the output of the model to determine the threshold.
In practice, we fix the material to be ‘D36’, the location to be ‘Beijing’ and the time to be ‘1 year’. Then, when the values of six environmental factors are sequentially changed, the model is used to predict the corresponding corrosion rate.
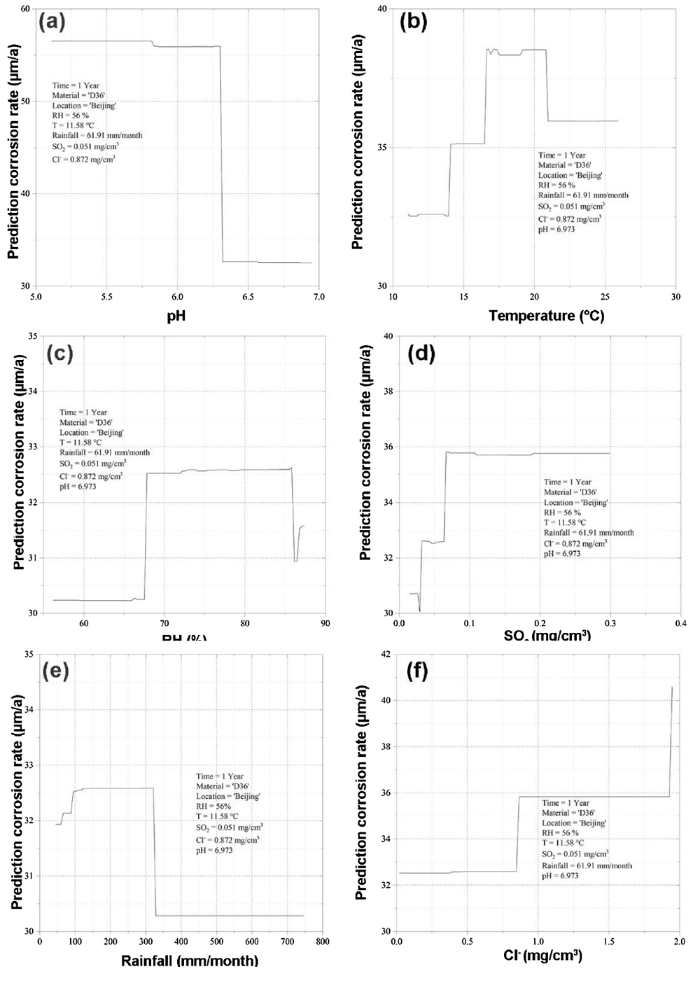
Fig. 6 shows the thresholds circumstance for 6 environmental factors.
Fig. 6.
Fig. 6.
Prediction corrosion rate curve with changing single environmental variable: Effects of pH thresholds (a), temperature thresholds (b), RH thresholds (c), SO2 thresholds (d), rainfall thresholds (e) and Cl- thresholds (f).
According to Fig. 6, we can infer qualitative and quantitative effects on the environmental factors to corrosion:
(1)As we know, when pH value decreases, the corrosion process will accelerate, due to the thin electrolyte film with lower pH could promote the dissolution of metal, destroy absorbed protective corrosion production layer [43,44]. Besides it, previous studies have shown that when pH value is less than a critical threshold, the corrosion of materials will be in an acidic environment, and the corresponding corrosion chemical reaction will be more intense than the reaction in a neutral environment, resulting in a faster corrosion process and corrosion rate [45]. However, due to the complexity of the corrosion process, it is often difficult to determine the pH threshold. With the help of the method in this paper, not only the qualitative analysis can be made, but also the corresponding quantitative results can be calculated. Just in Fig. 6(a), the pH threshold of D36 in Beijing area is about 6.3.
(2)Fig. 6(b) shows the predicted change curve of corrosion rate of D36 in Beijing with single temperature value changing. As for the influence of temperature on corrosion, experts believe that temperature can improve the chemical reaction process. On the other hand, the temperature will also increase the evaporation process of electrolyte film on the material surface, reduce the existence time of electrolyte film so as to reduce the corrosion rate. At present, some corrosion test results show the following phenomenon [46]. When the temperature is less than a critical threshold range, the increase of temperature will increase the corrosion rate of the material. When the temperature is higher than the threshold, the corrosion rate will be reduced. This phenomenon is consistent with the curve in Fig. 6(b), and the temperature threshold of D36 in Beijing is about 21℃.
(3)As we all know, the RH has an important effect on atmospheric corrosion, as well as oxygen. The RH can form electrolyte film which is necessary for atmospheric corrosion to occur. The previous studies generally showed that a thick electrolyte film could hinder the oxygen transport, lowering the cathodic corrosion rates; however, when the electrolyte film was too thin, it can hardly form an effective and continuous electrolyte for corrosion reactions [47]. Therefore, there are two critical RH values. One of them can be applied to determine whether the electrolyte film is continuous or not, and the other is used to decide whether the film is saturated or not. Based on Fig. 6(c), it can be seen that for the corrosion of D36 in Beijing, the paper gives two critical RH values are 67 % and 86 %.
(4)SO2 can improve the ion concentration in the electrolyte film, and catalyze the corrosion process [41,42]. Therefore, the higher SO2 corresponds to the higher corrosion rate, which is consistent with the curve trend in Fig. 6(d). In addition, the paper gives a threshold of SO2 around 0.067 mg/cm3, which can lead to the sudden change of corrosion rate.
(5)Similar to the effect of temperature on corrosion, rainfall raise can increase the RH and the electrolyte film on the surface of metal, and make the corrosion rate increase. On the other hand, excessive rainfall will wash away contaminants of metal surface frequently, which could decrease the corrosion rate [41,48]. The Fig. 6(e) give a threshold of rainfall is around 320 mm/month, and when rainfall value is over that threshold, the corrosion rate decreases sharply.
Depending on the data-modelling and mining, the paper attempts to give the effects of 6 environmental factors to outdoor atmospheric corrosion, while difficult to be obtained by corrosion experiment before. The results in Fig. 6 provide a corrosion trend of material ‘D36’ in ‘Beijing’ when a single environmental value is changed. Besides, the results also give a threshold for each environmental factor, which has a great important effect to the corrosion process. It can provide a new thought for the corrosion research field.
5. Conclusions
A new deep-structure model called DCCF-WKNNs is proposed in this paper to implement the corrosion modelling and knowledge mining. The main conclusions are in the following:
(1)To the task of corrosion modelling and prediction of various materials in a variety of outdoor atmospheric environments, the paper proposes a new deep model based on random forests model. Compared with the prediction results of several machine-learning algorithms on the collected low-alloy steels corrosion samples, the proposed method can obtain the best generalization performance.
(2)With the help of the proposed method, the paper draws a series of prediction corrosion rate curves when single environmental variable value changes. Based on the curves, we discover the thresholds of each variable, upon which the corrosion rates vary sharply.
(3)The development of the proposed DCCF-WKNNs on corrosion datasets provides a useful tool for the modelling and knowledge-mining of LAS corrosion in outdoor atmospheric.
Limited by the lack of quantitative of LAS microstructure in the collected datasets, the paper has not discussed the effects of chemical composition and microstructure on the corrosion in details. The related work will be further studied in the near future.
Acknowledgments
This work was financially supported by the National Key R&D Program of China (No. 2017YFB0702100) and the National Natural Science Foundation of China (No. 51871024). The authors also thank the China Corrosion and Protection Gateway for the data support.
Reference
DOI URL PMID [Cited within: 1]
DOI
URL
PMID
[Cited within: 3]

This study attempted to predict corrosion current density in concrete using artificial neural networks (ANN) combined with imperialist competitive algorithm (ICA) used to optimize weights of ANN. For that reason, temperature, AC resistivity over the steel bar, AC resistivity remote from the steel bar, and the DC resistivity over the steel bar are considered as input parameters and corrosion current density as output parameter. The ICA-ANN model has been compared with the genetic algorithm to evaluate its accuracy in three phases of training, testing, and prediction. The results showed that the ICA-ANN model enjoys more ability, flexibility, and accuracy.
Random forests are a combination of tree predictors such that each tree depends on the values of a random vector sampled independently and with the same distribution for all trees in the forest. The generalization error for forests converges a.s. to a limit as the number of trees in the forest becomes large. The generalization error of a forest of tree classifiers depends on the strength of the individual trees in the forest and the correlation between them. Using a random selection of features to split each node yields error rates that compare favorably to Adaboost (Y. Freund & R. Schapire, Machine Learning: Proceedings of the Thirteenth International conference, ***, 148–156), but are more robust with respect to noise. Internal estimates monitor error, strength, and correlation and these are used to show the response to increasing the number of features used in the splitting. Internal estimates are also used to measure variable importance. These ideas are also applicable to regression.]]>
Ensemble Methods Foundations and Algorithms, Chapman and Hall/CRC
AbstractThis paper proposes, focusing on random forests, the increasingly used statistical method for classification and regression problems introduced by Leo Breiman in 2001, to investigate two classical issues of variable selection. The first one is to find important variables for interpretation and the second one is more restrictive and try to design a good parsimonious prediction model. The main contribution is twofold: to provide some experimental insights about the behavior of the variable importance index based on random forests and to propose a strategy involving a ranking of explanatory variables using the random forests score of importance and a stepwise ascending variable introduction strategy.]]>
Proceedings of IEEE International Conference on Advances in Computing, Communications and Informatics
Proceeding of the 26th International Joint Conference on Artificial Intelligence
DOI
URL
PMID
[Cited within: 1]

Metal roofs are recognized for conveying significant metal loads to urban streams through stormwater runoff. Metal concentrations in urban runoff depend on roof types and prevailing weather conditions but the combined effects of roof age and rainfall pH on metal mobilization are not well understood. To investigate these effects on roof runoff, water quality was analysed from galvanized iron and copper roofs following rainfall events and also from simulating runoff using a rainfall simulator on specially constructed roof modules. Zinc and copper yields under different pH regimes were investigated for two roof materials and two different ages. Metal mobilization from older roofs was greater than new roofs with 55-year-old galvanized roof surfaces yielding more Zn, on average increasing by 45% and 30% under a rainfall pH of 4 and 8, respectively. Predominantly dissolved (85-95%) Zn and Cu concentrations in runoff exponentially increased as the rainfall pH decreased. Results also confirmed that copper guttering and downpipes associated with galvanized steel roof systems can substantially increase copper levels in roof runoff. Understanding the dynamics of roof surfaces as a function of weathering and rainfall pH regimes can help developers with making better choices about roof types and materials for stormwater improvement.
Ensemble of classifiers constitutes one of the main current directions in machine learning and data mining. It is accepted that the ensemble methods can be divided into static and dynamic ones. Dynamic ensemble methods explore the use of different classifiers for different samples and therefore may get better generalization ability than static ensemble methods. However, for most of dynamic approaches based on KNN rule, additional part of training samples should be taken out for estimating “local classification performance” of each base classifier. When the number of training samples is not sufficient enough, it would lead to the lower accuracy of the training model and the unreliableness for estimating local performances of base classifiers, so further hurt the integrated performance. This paper presents a new dynamic ensemble model that introduces cross-validation technique in the process of local performances’ evaluation and then dynamically assigns a weight to each component classifier. Experimental results with 10 UCI data sets demonstrate that when the size of training set is not large enough, the proposed method can achieve better performances compared with some dynamic ensemble methods as well as some classical static ensemble approaches.




 WeChat
WeChat