Structure Heterogeneity in Metallic Glass: Modeling and Experiment

Cite this Article

Ke H.B., Zeng J.F., Liu C.T., Yang Y.. Structure Heterogeneity in Metallic Glass: Modeling and Experiment. Journal of Materials Science & Technology, 2014, 30(6): 560-565 Copy to clipboard

Permissions

Structure Heterogeneity in Metallic Glass: Modeling and Experiment

Ke H.B., Zeng J.F., Liu C.T., Yang Y.^*

Centre for Advanced Structural Materials, Department of Mechanical and Biomedical Engineering, City University of Hong Kong, Kowloon Tong, Kowloon, Hong Kong, China

Corresponding author. Ph.D.; Tel.: +852 3442 9394

Abstract

Despite the great efforts dedicated to metallic glasses (MGs), their structure still remains a mystery to be understood. With comparison to the existing micromechanical models, such as the free-volume and shear transformation zone (STZ) models, we first discuss in this article our recently proposed ‘core-shell’ model, which contains a solid-like matrix and liquid-like inclusions. This serves as the theoretical basis to understand the structural heterogeneity in MGs in our analytical framework. After that, a scanning ultrafast nanoindentation technique is used to map out the structure heterogeneity in a Zr-based bulk metallic glass (BMG). With these ongoing research efforts, we hope that more research work could be stimulated in the pursuit of the structure-property relation in MGs.

Keyword: Metallic glass; Structure heterogeneity; Nanoindentation; Core-shell model

Show Figures

1. Introduction

Metallic glasses (MGs) are amorphous metals lacking a long-range translational symmetry in their atomic structure. Over the past decades, MGs have been extensively studied due to their excellent mechanical and physical properties^{[1], [2], [3] and [4]}, and are therefore considered to be a candidate material for a variety of structural and functional applications^{[5], [6] and [7]}. However, owing to the structural complexity, the deformation mechanisms in MGs have not yet been fully understood, which still remain as a topic of active research today.

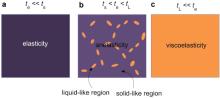
In the nominal elastic regime, MGs appear to deform in the same way as traditional crystalline metals. However, the recent experiments have shown that MGs actually undergo anelastic deformation in their apparent elastic regime even at room temperature^{[8], [9], [10], [11], [12] and [13]}. For instance, through the analysis of the X-ray diffraction results, Dmowski et al. suggested that a quarter of the apparently elastic response of an MG is indeed anelastic ^[8]; Ye et al. also discovered that MGs are not fully elastically loaded in this apparent elastic regime as significant mechanical hysteresis would occur if dynamic loading was exerted on MG micro-samples ^[9]. Since anelasticity arises as a consequence of elastic and inelastic deformation, which signals structural heterogeneity below a certain length scale, all these results thus indicate that the amorphous structure of MGs is indeed heterogeneous, namely, it comprises liquid- and solid-like regions which deform in a distinctive manner upon mechanical loading. The former acts as viscous flow units for energy dissipation while the latter as an elastic ‘scaffold’.

In the MG literature, the two widely used mean-field models for understanding the atomic-scale plastic flow in MGs, namely, the free volume ^[14] and shear transformation zone (STZ) model^{[15] and [16]}, were developed in the 1970s. Although these two models share a similar mathematic framework and have been successfully used to explain many important deformation features, such as shear localization or shear-band formation from the perspective of shear-induced softening/dilation ^[17], however, their physical basis has also been constantly debated through the comparison with the atomistic simulations and experimental results obtained recently^{[18] and [19]}.

According to the STZ models^{[15] and [16]}, plastic flow occurs in MGs via the STZ event or the activation of the potential STZ site, which consists of a cluster of atoms moving collectively under shear ( Fig. 1(a)). Following the modified STZ model of Falk and Langer ^[16], an STZ site in MGs could be viewed as the elementary plasticity ‘carrier’ as an analog of the dislocation in a crystalline metal. Nevertheless, unlike dislocations being a structural defect that can be characterized by electron microscopy, the presence of STZs cannot be observed in advance unless they are externally perturbed. Alternatively, the atomic-scale plastic flow in MGs could be modeled following the “free volume” theory as proposed by Spaepen ^[14]. According to the free-volume model, plastic flow occurs via the discrete atomic jumps in and out of the free-volume site, as depicted schematically in Fig. 2(b). During this process of local diffusive jumps, free volumes could be created and annihilated, leading to the macroscopically observable plastic flow. Note that the above two kinds of models, as originally developed for yielding and plasticity in MGs, were all of a mean-field type. Therefore, any possible structural interactions were neglected. Here, the pre-yield deformation was taken as a trivial process of elasticity; yielding occurs once STZs or free-volume creation is activated without considering any non-local structural interactions.

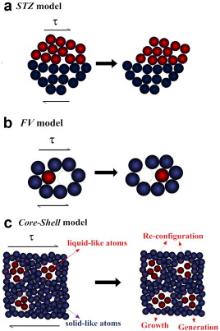	Figure Option View Download New Window
	Fig. 1. Schematics of (a) the shear transformation zone (STZ) model, after Argon, (b) the free volume (FV) model, after Spaepen, and (c) the core-shell model proposed by us.

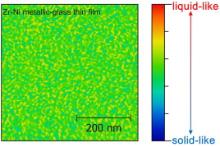	Figure Option View Download New Window
	Fig. 2. DAFM image obtained from a Zr–Ni metallic-glass thin film showing the structural contrast as determined from the ability of anelastic energy dissipation (the blue region = the solid-like region with low energy dissipation and the red region = the liquid-like region with high energy dissipation). Note that the image is adapted from Ref ^[26].

As inspired by the phenomenon of anelasticity ^[9] and the vast previous atomistic simulations^{[20], [21], [22], [23] and [24]}, we proposed a core-shell structural model in our previous work to rationalize the pre-yield deformation behavior of MGs^{[9], [25], [26] and [27]}. As shown in Fig. 1(c), the atomic structure, as depicted in the core-shell model, is composed of liquid-like atoms (red spheres) and solid-like atoms (blue spheres). To retain an overall solid-like characteristic in the glass, the solid-like atoms must percolate and form an elastic network, while the liquid-like ones are therefore encaged as ‘inclusions’ or ‘flow units’. Different from the free-volume or STZ model, the core-shell model explicitly takes into account the elastic back-stress effect from the solid-like atoms, therefore explaining the anelasticity naturally^{[9], [25], [26], [27] and [28]}. Furthermore, as all liquid-like atoms can be modeled as a liquid-like ‘phase’ interacting with its elastic ‘shell’ from a coarse-grained perspective, the core-shell model is essentially a non-local approach. From a theoretical point of view, it can be perceived that, in the ‘elastic’ regime, an existing liquid-like region may grow or reconfigure itself, or a new liquid-like region may be generated as long as the elastic ‘shell’ still remains interconnected ( Fig. 1(c)). This is a much richer picture of deformation dynamics involving structural evolution as compared to those in the original STZ or free-volume model, which is much closer to what the atomistic simulations already revealed.

To confirm the above thinking, dynamic atomic force microscopy (DAFM) was recently used to probe the surface of the metallic-glass thin films (MGTFs)^{[26], [29] and [30]}. According to the anelastic energy dissipation measured at each individual contact between the AFM tip and the MGTF, the structural heterogeneity in MGs could be revealed. Fig. 2 shows a typical DAFM structural picture obtained from a Zr–Ni MGTF ^[26], from which one can clearly see a structural contrast resulting from the varying degree of anelastic energy absorption over the scanned surface. As the force exerted by the AFM tip is usually very small, we expect that the DAFM technique retains the overall feature of the atomic structure before the perturbation. In the literature, the DAFM technique was already utilized to characterize the structural heterogeneity^{[29] and [30]} and to study the annealing-induced fractal-like densification process in the MGTF ^[26].

While the DAFM is a useful technique, however, it usually demands an atomic-scale surface smoothness^{[26] and [29]}, hence limiting its application to bulk metallic glasses (BMGs). Furthermore, the DAFM method is essentially an amplitude rather than force modulation technique; hence, it is very hard to quantitatively extract the local mechanical properties, such as the local modulus for the elastic ‘shell’, and the local viscosity for the viscous ‘core’. In this study, we would like to propose a nanoindentation based method to characterize the structure heterogeneity in BMGs. With a well-controlled load function, the spatial mapping of local modulus, local viscosity and local relaxation time is enabled, which provides an experimental means, alternative to the DAFM technique, in the exploration of the structure and the structure-property relation in BMGs.

2. Theoretical

According to the core-shell model^{[25] and [26]} ( Fig. 3(a)), the stress-induced activation of the individual viscous core is a probabilistic process. The activation probability, p, can be related to the external shear stress, τ, as follows:

$\frac{d p}{d t} + 2 ω p e^{- \frac{Δ G}{k T}} = 2 ω e^{- \frac{Δ G}{k T}} \frac{τ Ω}{k T}$ (1)

where ω= the attempt frequency of the liquid-like atoms, Δ G= the energy barrier against the activation, t= the time, k= the Boltzmann constant, T= the ambient temperature, and Ω= the activation volume.

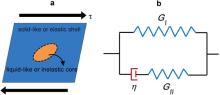	Figure Option View Download New Window
	Fig. 3. Schematics of (a) the coarse-grained core-shell model and (b) the standard linear solid (SLS) rheological model that gives rise to the same governing equation as (a).

The total mechanical strain, γ, occurring to the MG can be approximated as the sum of the affine (elastic) strain, γ_e = σ/ μ, and the non-affine (inelastic) strain γ_i ∼ βp, where μ is the shear modulus of the solid-like shell and β is the pre-factor that quantifies the sensitivity of the total strain to its inelastic component β = ∂ γ/∂ γ_i. Substituting γ = τ/ μ + βp into (1) gives:

$\dot{γ} + 2 ω e^{- \frac{Δ G}{k T}} γ = \frac{\dot{τ}}{μ} + 2 ω e^{- \frac{Δ G}{k T}} (\frac{β Ω}{k T} + \frac{1}{μ}) τ$ (2)

Note that Eq.(2) is a typical equation that can be derived from the standard linear solid (SLS) model in rheology, which is composed of two springs and one dashpot, as shown in Fig. 3(b). After translating the variety of physical parameters related to the liquid- and solid-like atoms into the spring moduli, G_I and G_II, and the dashpot viscosity η, we obtain

$\dot{γ} + \frac{G_{I} G_{II}}{η (G_{I} + G_{II})} γ = \frac{\dot{τ}}{G_{I} + G_{II}} + \frac{G_{II}}{η (G_{I} + G_{II})} τ$ (3A)

$G_{I} = μ / (1 + α)$ (3B)

$G_{II} = α μ / (1 + α)$ (3C)

$η = \frac{α μ}{2 ω e^{- Δ G / k T} \cdot {(1 + α)}^{2}}$ (3D)

where α= βΩμ/( kT) can be viewed as a state variable that increases with the total volume of the liquid-like atoms in an MG. Theoretically, there are two limiting cases, i.e. α= 0 and α= infinity. The former case corresponds to an ‘ideal’ or ‘perfect’ glass without the liquid-like atoms ^[31], while the latter to a ‘pure’ liquid without any solid-like atoms. For these two cases, we have

$Elasticity for the'ideal' glass : \dot{γ} = \frac{\dot{τ}}{G_{I}}$ (4A)

$Maxwell-typed viscoelasticity for the'pure' liquid : \dot{γ} = \frac{\dot{τ}}{G_{II}} + \frac{τ}{η}$ (4B)

Hence, anelasticity in MGs can be viewed as an intermediate case where some ‘residual liquidity’ is embedded into the ideal glass owing to the fast cooling.

3. Experimental

Once the theoretical basis is clear, now let us discuss how we can use the state-of-art nanoindentation technique to detect the presence of the liquid- and solid-like regions, namely, to measure the local viscosity η and the local modulus G_I or G_II. For this purpose, a typical Zr-based BMG with the nominal composition of Zr_52.5Ti₅Cu_17.9Ni_14.6Al₁₀ (Vit105) was selected as the model material. Prior to indentation, the amorphous structure of the sample was confirmed by X-ray diffraction and differential scanning calorimetry ^[25] (not shown here) and the sample surface was mechanically polished to a mirror finish. The nanoindentation scanning of 11 × 11 points was subsequently performed on the TI 950 TriboIndenter system (Hysitron Inc., Minneapolis, MN) with a 2 μm spherical indenter at room temperature, as illustrated in Fig. 4(a). At each indentation point, we employed a load function featured with an asymmetric loading–holding–unloading profile, as shown in Fig. 4(b). In virtue of the ultrafast data acquisition capability (with a maximum of 30,000 points per second) of the nanoindentation system, unusually high loading rates could be achieved. In order to reveal the effect of anelasticity, the loading time t_L, the holding time t_H and unloading time t_U, were both fixed at 0.001 s, 0.1 s and 0.1 s, respectively. The holding time is significantly larger than the loading time to ensure the full recovery of the anelastic deformation caused by the fast loading.

Figure Option
'>View Download New Window

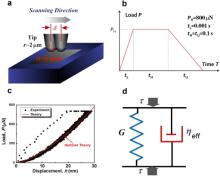Fig. 4. (a) Schematic illustration of the scanning nanoindentation test to map out the structural heterogeneity in a BMG, (b) the sketch of the indentation load function, (c) the representative nanoindentation P–h curves obtained at P_H = 800 μN, showing the anelastic deformation in the Vit105 BMG. The Hertzian curve (red line) corresponds to the indenter tip radius of 2 μm, shear modulus of 30 GPa and Poisson's ratio of 0.363 for Vit105, (d) the sketch of the effective Kelvin model.

Fig. 4(c) displays the typical load-displacement curves obtained by indenting the Zr-based BMG at a constant load of 800 μN, from which it can be seen that all curves return to the zero displacement after unloading, implicative of the elastic nature of the material's response. Furthermore, it can be seen that the loading curves deviate significantly from the Hertzian theory owing to the anelastic nature of the deformation. During the holding time, the material ‘creeps’ to the corresponding Hertzian point and then follows the Hertzian response during unloading. Note that, in a load-controlled experiment, the stress rate $\dot{τ}$ can be approximated as zero at a small indentation load. This is because the time spent for a load increment in the nanoindentation is longer than the relaxation time of the liquid-like region. For details of discussion, please refer to our previous work ^[25]. Hence, Eq. could be simplified to a Kelvin model ( Fig. 4(d)):

$\dot{γ} + \frac{G_{I} G_{II}}{η (G_{I} + G_{II})} γ = \frac{G_{II}}{η (G_{I} + G_{II})} τ$ (5A)

$or simply \dot{γ} + \frac{G}{η_{e f f}} γ = \frac{τ}{η_{e f f}}$ (5B)

where G= G_Iand the effective viscosity η_eff= η(1 + G_I/G_II) = η(1 + 1/ α).

For an elastic Hertzian contact, the load-displacement relation can be expressed as

$h {(t)}^{3/2} = 3 P (1 - ν) / 8 G \sqrt{R}$ (6)

where his the indent depth; Pis the indentation load; vis the material's Poisson's ratio; Gis the material's shear modulus; and Ris the indenter tip radius. For an anelastic solid as shown in Fig. 4(d), the loading curve can be derived from the Hertzian solution using the integral transform method ^[32]:

$h {(t)}^{3/2} = h_{0} {(t)}^{3/2} - \frac{3 \dot{P} (1 - ν) t_{c}}{8 \sqrt{R} G} [1 - \exp (- \frac{t}{t_{c}})]$ (7)

where $\dot{P}$ is the loading rate; t_c= η/ Gis the relaxation time of the liquid-like region; and h₀is the Hertzian solution $h_{0} {(t)}^{3/2} = 3 P (t) (1 - ν) / 8 G \sqrt{R}$ . For simplicity, a constant Poisson's ratio of 0.363 is assumed for the derivation. By fitting the experiment data to Eqs.(6)and(7), we can obtain the shear modulus Gand the relaxation time t_cpoint by point. After that, the local viscosity η_effcan be also computed from t_c= η_eff/ G. Therefore, we can obtain the local shear modulus G, the local relaxation time t_cand the local viscosity η_effall from a single indentation experiment.

4. Results and Discussion

4.1. Mapping of structural heterogeneity in BMG

Following the above method, the nanoindetation tests were repeated at 11 × 11 different positions in a square lattice with a spacing of 100 nm Fig. 5(a)–(c) shows the mapping of the local shear modulus, the local relaxation time and the local viscosity as obtained from the ultra-fast spherical indentation experiments. As seen in this figure, the tested amorphous structure exhibits the variations in not only the local static property, such as the shear modulus, but also the local dynamic properties, such as the local viscosity or relaxation time. Due to the limited spatial resolution (~100 nm) of the current experimental settings, a sudden or discontinuous change in these measured local properties can be witnessed. Despite that, the general trend of a local structural heterogeneity is still perceivable. Fig. 5(d)–(f) displays the statistical distributions of G, t_c and η_eff, all of which can be fitted to a Gaussian curve. Again, this distribution is expected and agrees with the previous findings with respect to the distribution of local properties in MGs^{[20] and [33]}.

	Figure Option View Download New Window
	Fig. 5. Mapping of (a) local shear modulus, (b) local relaxation time and (c) local viscosity of the Zr-based BMG at the indentation load of 800 μN and the scanning space of 100 nm. On the right are the corresponding statistical distribution of (d) local shear modulus, (e) local relaxation time and (f) local viscosity. The dashed lines are the Gaussian fitting to the experimental data.

4.2. Local versus global viscosity in BMG

According to our ultra-fast indentation experiment, the typical value for the local viscosity is around 10⁷ Pa s for the liquid-like regions in the Zr-based BMG, which corresponds to a relaxation time t_c ~ 0.4 ms being encaged by an elastic ‘shell’ with a shear modulus G ~ 30 GPa. These results are consistent with the previous findings^{[9] and [25]}. Now one may ask the following questions: (1) why do some atoms behave solid-like while others liquid-like although the atomic packing is amorphous everywhere in the glass; and (2) since the viscosity of supercooled liquids already reaches up to 10¹² Pa s at the glass transition point, how come the viscosity in the glass could be such low, only around 10⁷ Pa s?

Now let us address the first question. According to Ref. ^[34], glass transition can be viewed as a percolation process in which the slowly relaxing atoms, which corresponds to a large viscosity and a long relaxation time t_L, percolate to form the ‘skeleton’ of the glass whilst the rapidly relaxing atoms, which corresponds to a low viscosity and a short relaxation time t_s (<< t_L), are therefore left as the ‘residual liquidity’ embedded in the glass. In such a case, we may term the viscosity of the percolating atoms as the global viscosity as opposed to the local viscosity of the liquid-like atoms. Given an experimental time scale t_e, all atoms would behave elastically if t_e << t_s ( Fig. 6(a)). In such a case, the glass appears as a pure elastic solid. On the other hand, if t_s < t_e << t_L, structural heterogeneity can be easily detected due to the distinction between the liquid- and solid-like atoms ( Fig. 6(b)). Finally, if t_L << t_e, all atoms appear ‘flowing’ under stress like in a liquid state, as illustrated in Fig. 6(c). According to the recent room temperature creep tests^{[10] and [11]}, we can roughly estimate that the relaxation time of the solid-like regions is about 10⁴–10⁵ s and the associated viscosity is about 10¹⁵–10¹⁶ Pa s when the external stress reaches about 90% of the yielding strength. According to Guan et al. ^[35], the viscosity and relaxation time of the solid-like regions could be even higher at a smaller stress. Because the experimental time is finite, say, t_e ∼ 0.2 s as in our indentation experiments, the atoms corresponding to a high viscosity or a long relaxation time (>10⁵ s) therefore behave like elastic solids. Furthermore, the local structural motif may differ between the liquid- and solid-like atoms, which can also explain the large variation between the local and global viscosity. Following this line of reasoning, it can be understood that the viscosity measured for the supercooled liquid should correspond to the global viscosity of the whole glass while the viscosity we herein measured only should correspond to the local one. This distinction between the local and global viscosity is indeed the dynamic nature of structural heterogeneity in MGs.

	Figure Option View Download New Window
	Fig. 6. Schematic illustrations of the possible ‘elastic’ behaviors that an MG alloy could exhibit according to the pre-set experimental time t_e relative to the two internal relaxation times ( t_s and t_L): (a) pure elasticity ( t_e << t_s), (b) anelasticity ( t_s < t_e < t_L), and (c) viscoelasticity ( t_L << t_e).

5. Summary

To summarize, our current work can be divided into two parts. In the first part, we briefly discuss the physics and mathematical formulation of the core-shell model in comparison to the traditional free volume and STZ models. The core-shell modeling is based on the notion that there is distinction between the solid- and liquid-like atoms in the glass. As a coarse-grained approach, the core-shell model can be also applied to study the structural evolution in MGs. In the second part, we discuss the use of a nanoindentation method as in align with our core-shell model to characterize the structure heterogeneity in BMGs. Our preliminary results show that the local modulus, the local relaxation time and the local viscosity could be all mapped out simultaneously on a two-dimensional plane. This scanning ultrafast indentation method is a promising technique to characterize different amorphous structures in BMGs in terms of their local static and dynamic properties.

References

Acknowledgments

Y. Yang is grateful to the financial support provided by City University of Hong Kong (CityU) through the start-up grant for newly recruited faculty members (Project No. 7200303) and the research of C.T. Liu is also supported by CityU (Project No. CityU117612).

The authors have declared that no competing interests exist.

Reference

View Option

1.	M. W. Chen, Annu. Rev. Mater. Res. , 38 (2008), pp. 445–469 [Cited within: 1]
2.	C. A. Schuh, T. C. Hufnagel, U. Ramamurty, Acta Mater. , 55 (2007), pp. 4067–4109 [Cited within: 1] [JCR: 3.941]
3.	M. M. Trexler, N. N. Thadhani, Prog. Mater. Sci. , 55 (2010), pp. 759–839 [Cited within: 1] [JCR: 23.194]
4.	A. R. Yavari, J. J. Lewand owski, J. Eckert, MRS Bull. , 32 (2007), pp. 635–638 [Cited within: 1] [JCR: 5.024]
5.	A. L. Greer, E. Ma, MRS Bull. , 32 (2007), pp. 611–619 [Cited within: 1] [JCR: 5.024]
6.	W. H. Wang, Adv. Mater. , 21 (2009), pp. 4524–4544 [Cited within: 1] [JCR: 14.829]
7.	G. Kumar, A. Desai, J. Schroers, Adv. Mater. , 23 (2011), pp. 461–476 [Cited within: 1] [JCR: 14.829]
8.	W. Dmowski, T. Iwashita, C. P. Chuang, J. Almer, T. Egami, Phys. Rev. Lett. , 105 (2010), p. 205502 [Cited within: 2] [JCR: 7.943]
9.	J. C. Ye, J. Lu, C. T. Liu, Q. Wang, Y. Yang, Nat. Mater. , 9 (2010), pp. 619–623 [Cited within: 6] [JCR: 35.749]
10.	H. B. Ke, P. Wen, H. L. Peng, W. H. Wang, A. L. Greer, Scripta Mater. , 64 (2010), pp. 966–969 [Cited within: 2] [JCR: 2.821]
11.	K. W. Park, C. M. Lee, M. Waked, Y. Shibutani, M. L. Falk, J. C. Lee, Acta Mater. , 56 (2008), pp. 5440–5450 [Cited within: 2] [JCR: 3.941]
12.	W. Jiao, P. Wen, H. L. Peng, H. Y. Bai, B. A. Sun, W. H. Wang, Appl. Phys. Lett. , 102 (2013), p. 101903 [Cited within: 1] [JCR: 3.794]
13.	W. Jiao, B. A. Sun, P. Wen, H. Y. Bai, Q. P. Kong, W. H. Wang, Appl. Phys. Lett. , 103 (2013), p. 081904 [Cited within: 1] [JCR: 3.794]
14.	F. Spaepen, Acta Metall. , 25 (1977), pp. 407–415 [Cited within: 2] [JCR: 0.612] [CJCR: 0.835]
15.	A. S. Argon, Acta Metall. , 27 (1979), pp. 47–58 [Cited within: 2] [JCR: 0.612] [CJCR: 0.835]
16.	M. L. Falk, J. S. Langer, Phys. Rev. E, 57 (1998), pp. 7192–7205 [Cited within: 3] [JCR: 2.313]
17.	A. L. Greer, Y. Q. Cheng, E. Ma, Mater. Sci. Eng. R, 74 (2013), pp. 71–132 [Cited within: 1]
18.	T. Egami, J. Alloy. Compd. , 509 (2011), pp. [Cited within: 1] [JCR: 2.39]
19.	R. Dasgupta, S. Karmakar, I. Procaccia, Phys. Rev. Lett. , 108 (2012), p. 075701 [Cited within: 1] [JCR: 7.943]
20.	T. Egami, D. Srolovitz, J. Phys. F, 12 (1982), pp. 2141–2163 [Cited within: 2]
21.	J. L. Barrat, J. J. de Pablo, MRS Bull. , 32 (2007), pp. 941–944 [Cited within: 1] [JCR: 5.024]
22.	S. Takeuchi, K. Edagawa, Prog. Mater. Sci. , 56 (2011), pp. 785–816 [Cited within: 1] [JCR: 23.194]
23.	Y. Q. Cheng, E. Ma, Prog. Mater. Sci. , 56 (2011), pp. 379–473 [Cited within: 1] [JCR: 23.194]
24.	H. L. Peng, M. Z. Li, W. H. Wang, Appl. Phys. Lett. , 102 (2013), p. 131908 [Cited within: 1] [JCR: 3.794]
25.	L. S. Huo, J. F. Zeng, W. H. Wang, C. T. Liu, Y. Yang, Acta Mater. , 61 (2012), pp. 4329–4338 [Cited within: 6] [JCR: 3.941]
26.	Y. Yang, J. F. Zeng, A. Volland , J. J. Bland in, S. Gravier, C. T. Liu, Acta Mater. , 60 (2012), pp. 5260–5272 [Cited within: 7] [JCR: 3.941]
27.	Y. Yang, J. F. Zeng, J. C. Ye, J. Lu, Appl. Phys. Lett. , 97 (2010), p. 261905 [Cited within: 2] [JCR: 3.794]
28.	Z. Y. Liu, Y. Yang, C. T. Liu, Acta Mater. , 61 (2013), pp. 5928–5936 [Cited within: 1] [JCR: 3.941]
29.	J. F. Zeng, J. P. Chu, Y. C. Chen, A. Volland , J. J. Bland in, S. Gravier, Y. Yang, Intermetallics, 44 (2014), pp. 121–127 [Cited within: 3] [JCR: 1.857]
30.	Y. H. Liu, D. Wang, K. Nakajima, W. Zhang, A. Hirata, T. Nishi, A. Inoue, M. W. Chen, Phys. Rev. Lett. , 106 (2011), p. 125504 [Cited within: 2] [JCR: 7.943]
31.	Z. Wang, P. Wen, L. S. Huo, H. Y. Bai, W. H. Wang, Appl. Phys. Lett. , 101 (2012), p. 121906 [Cited within: 1] [JCR: 3.794]
32.	R. M. Christensen, Dover Publications, New York, 1982. [Cited within: 1]
33.	H. Wagner, D. Bedorf, S. Küchemann, M. Schwabe, B. Zhang, W. Arnold, K. Samwer, Nat. Mater. , 10 (2011), pp. 439–442 [Cited within: 1] [JCR: 35.749]
34.	H. Tanaka, T. Kawasaki, H. Shintani, K. Watanabe, Nat. Mater. , 9 (2010), pp. 324–331 [Cited within: 1] [JCR: 35.749]
35.	P. F. Guan, M. W. Chen, T. Egami, Phys. Rev. Lett. , 104 (2010), p. 205701 [Cited within: 1] [JCR: 7.943]

2008

0.0

... Over the past decades, MGs have been extensively studied due to their excellent mechanical and physical properties^{[1], [2], [3] and [4]}, and are therefore considered to be a candidate material for a variety of structural and functional applications^{[5], [6] and [7]} ...

2007

3.941

0.0

C. A.

Schuh

, T. C.

Hufnagel

, U.

Ramamurty

, Acta Mater. , 55 (2007), pp. 4067–4109

Abstract The mechanical properties of amorphous alloys have proven both scientifically unique and of potential practical interest, although the underlying deformation physics of these materials remain less firmly established as compared with crystalline alloys. In this article, we review recent advances in understanding the mechanical behavior of metallic glasses, with particular emphasis on the deformation and fracture mechanisms. Atomistic as well as continuum modeling and experimental work on elasticity, plastic flow and localization, fracture and fatigue are all discussed, and theoretical developments are connected, where possible, with macroscopic experimental responses. The role of glass structure on mechanical properties, and conversely, the effect of deformation upon glass structure, are also described. The mechanical properties of metallic glass-derivative materials – including in situ and ex situ composites, foams and nanocrystal-reinforced glasses – are reviewed as well. Finally, we identify a number of important unresolved issues for the field.

2010

23.194

0.0

M. M.

Trexler

, N. N.

Thadhani

, Prog. Mater. Sci. , 55 (2010), pp. 759–839

Abstract The mechanical properties of bulk metallic glasses, including their superior strength and hardness, and excellent corrosion and wear resistance, combined with their general inability to undergo homogeneous plastic deformation have been a subject of fascination for scientists and engineers. The scientific interest stems from the unconventional deformation and failure initiation mechanisms in this class of materials in which the typical carriers of plastic flow (dislocations) are absent. Metallic glasses undergo highly localized, heterogeneous deformation by formation of shear bands, a particular mode of deformation of interest for certain applications, but which also causes them to fail catastrophically due to uninhibited shear band propagation. Varying degrees of brittle and plastic failure creating intricate fracture patterns are observed in metallic glasses, quite different from those observed in crystalline solids. The tension–compression anisotropy, strain-rate sensitivity, thermal stability, stress-induced crystallization and polyamorphism transformations, are some of the attributes that have sparked engineering studies on bulk metallic glasses. Understanding of the glass-forming ability and the deformation and failure mechanisms of bulk metallic glasses, has given insight into alloy compositions and intrinsically-forming or extrinsically-added reinforcement phases for creating composite structures, to attain the combination of high strength, tensile ductility, and fracture toughness needed for use in advanced structural applications. The relative ease of fabricating metallic glasses into bulk forms, combined with their unique mechanical properties, has made these materials attractive options for possible applications in aerospace, naval, sports equipment, luxury goods, armor and anti-armor systems, electronic packaging, and biomedical devices.

2007

5.024

0.0

2007

5.024

0.0

2009

14.829

0.0

2011

14.829

0.0

2010

7.943

0.0

... However, the recent experiments have shown that MGs actually undergo anelastic deformation in their apparent elastic regime even at room temperature^{[8], [9], [10], [11], [12] and [13]} ...

... suggested that a quarter of the apparently elastic response of an MG is indeed anelastic^[8] ...

2010

35.749

0.0

... However, the recent experiments have shown that MGs actually undergo anelastic deformation in their apparent elastic regime even at room temperature^{[8], [9], [10], [11], [12] and [13]} ...

... also discovered that MGs are not fully elastically loaded in this apparent elastic regime as significant mechanical hysteresis would occur if dynamic loading was exerted on MG micro-samples^[9] ...

... As inspired by the phenomenon of anelasticity^[9] and the vast previous atomistic simulations^{[20], [21], [22], [23] and [24]}, we proposed a core-shell structural model in our previous work to rationalize the pre-yield deformation behavior of MGs^{[9], [25], [26] and [27]} ...

... Different from the free-volume or STZ model, the core-shell model explicitly takes into account the elastic back-stress effect from the solid-like atoms, therefore explaining the anelasticity naturally^{[9], [25], [26], [27] and [28]} ...

... These results are consistent with the previous findings ^{[9] and [25]} ...

2010

2.821

0.0

... However, the recent experiments have shown that MGs actually undergo anelastic deformation in their apparent elastic regime even at room temperature^{[8], [9], [10], [11], [12] and [13]} ...

... According to the recent room temperature creep tests ^{[10] and [11]}, we can roughly estimate that the relaxation time of the solid-like regions is about 10⁴–10⁵ s and the associated viscosity is about 10¹⁵–10¹⁶ Pa s when the external stress reaches about 90% of the yielding strength ...

2008

3.941

0.0

K. W.

Park

, C. M.

Lee

, M.

Waked

, Y.

Shibutani

, M. L.

Falk

, J. C.

Lee

, Acta Mater. , 56 (2008), pp. 5440–5450

Abstract This study demonstrates that elastostatic compression imposed on amorphous alloys at room temperature induces irreversible structural disordering. The rate of disordering depends on the atomic packing density as determined by the fraction of the material in short-range ordered (SRO) atomic environments. The structural disordering, measured experimentally by differential scanning calorimetry, in turn alters the mechanical properties of the material. A combination of experiments and molecular dynamics simulations are used to explore fundamental issues related to shear-induced disordering during elastostatic compression.

... However, the recent experiments have shown that MGs actually undergo anelastic deformation in their apparent elastic regime even at room temperature^{[8], [9], [10], [11], [12] and [13]} ...

2013

3.794

0.0

... However, the recent experiments have shown that MGs actually undergo anelastic deformation in their apparent elastic regime even at room temperature^{[8], [9], [10], [11], [12] and [13]} ...

2013

3.794

0.0

... However, the recent experiments have shown that MGs actually undergo anelastic deformation in their apparent elastic regime even at room temperature^{[8], [9], [10], [11], [12] and [13]} ...

1977

0.612

0.835

... In the MG literature, the two widely used mean-field models for understanding the atomic-scale plastic flow in MGs, namely, the free volume^[14] and shear transformation zone (STZ) model^{[15] and [16]}, were developed in the 1970s ...

... Alternatively, the atomic-scale plastic flow in MGs could be modeled following the “free volume” theory as proposed by Spaepen^[14] ...

1979

0.612

0.835

... According to the STZ models^{[15] and [16]}, plastic flow occurs in MGs via the STZ event or the activation of the potential STZ site, which consists of a cluster of atoms moving collectively under shear (Fig ...

1998

2.313

0.0

... Following the modified STZ model of Falk and Langer^[16], an STZ site in MGs could be viewed as the elementary plasticity ‘carrier’ as an analog of the dislocation in a crystalline metal ...

2013

0.0

... Although these two models share a similar mathematic framework and have been successfully used to explain many important deformation features, such as shear localization or shear-band formation from the perspective of shear-induced softening/dilation^[17], however, their physical basis has also been constantly debated through the comparison with the atomistic simulations and experimental results obtained recently^{[18] and [19]} ...

2011

2.39

0.0

2012

7.943

0.0

1982

0.0

... Again, this distribution is expected and agrees with the previous findings with respect to the distribution of local properties in MGs ^{[20] and [33]} ...

2007

5.024

0.0

2011

23.194

0.0

Takeuchi

, K.

Edagawa

, Prog. Mater. Sci. , 56 (2011), pp. 785–816

Abstract Since the end of 1980s, bulk metallic glasses became available for various multi-component alloys. Because bulk metallic glasses are applicable to structural materials, their mechanical properties have become a matter of great interest in these decades. A characteristic feature of plastic deformation of metallic glasses at the ambient temperature is the localized shear deformation. Since we have no appropriate experimental technique, unlike crystalline matter, to approach microscopic deformation process in amorphous materials, we have to rely on computer simulation studies by use of atomistic models to reveal the microscopic deformation processes. In this article, we review atomistic simulation studies of deformation processes in metallic glasses, i.e., local shear transformation (LST), structural characterization of the local shear transformation zones (STZs), deformation-induced softening, shear band formation and its development, by use of elemental and metal–metal alloy models. We also review representative microscopic models so far proposed for the deformation mechanism: early dislocation model, Spaepen’s free-volume model, Argons’s STZ model and recent two-state STZ models by Langer et al.

2011

23.194

0.0

Y. Q.

Cheng

, E.

, Prog. Mater. Sci. , 56 (2011), pp. 379–473

Abstract The structure of metallic glasses (MGs) has been a long-standing mystery. On the one hand, MGs are amorphous materials with no long-range structural order; on the other hand, topological and chemical short-to-medium range order is expected to be pronounced in these alloys, due to their high atomic packing density and the varying chemical affinity between the constituent elements. The unique internal structure of MGs underlies their interesting properties, which render MGs potentially useful for various applications. While more and more glass-forming alloys have been developed in recent years, fundamental knowledge on the structural aspect of MGs remains seriously lacking. For example, how atoms pack on the short-to-medium range, how the structure differs in different MGs and changes with composition, temperature, and processing history, and more importantly, how the structure influences the properties of MGs, are still unresolved questions. In this paper, we review the tremendous efforts over the past 50 years devoted to unraveling the atomic-level structure of MGs and the structural origin of their unique behaviors. Emphasis will be placed on the progress made in recent years, including advances in structural characterization and analysis of prototypical MGs, general structural models and fundamental principles, and the correlations of thermodynamic, kinetic, and mechanical properties with the MG structures. Some widely observed property–property correlations in MGs are also examined from the structural perspective. The insights summarized are shown to shed light on many intriguing behaviors of the MG-forming alloys and expected to impact the development of MGs. Outstanding questions in this important research area will also be outlined.

2013

3.794

0.0

2012

3.941

0.0

... TheoreticalAccording to the core-shell model^{[25] and [26]} (Fig ...

... Prior to indentation, the amorphous structure of the sample was confirmed by X-ray diffraction and differential scanning calorimetry ^[25] (not shown here) and the sample surface was mechanically polished to a mirror finish ...

... For details of discussion, please refer to our previous work^[25] ...

... These results are consistent with the previous findings ^{[9] and [25]} ...

2012

3.941

0.0

... To confirm the above thinking, dynamic atomic force microscopy (DAFM) was recently used to probe the surface of the metallic-glass thin films (MGTFs)^{[26], [29] and [30]} ...

... 2 shows a typical DAFM structural picture obtained from a Zr–Ni MGTF^[26], from which one can clearly see a structural contrast resulting from the varying degree of anelastic energy absorption over the scanned surface ...

... In the literature, the DAFM technique was already utilized to characterize the structural heterogeneity^{[29] and [30]} and to study the annealing-induced fractal-like densification process in the MGTF^[26] ...

... While the DAFM is a useful technique, however, it usually demands an atomic-scale surface smoothness^{[26] and [29]}, hence limiting its application to bulk metallic glasses (BMGs) ...

... TheoreticalAccording to the core-shell model^{[25] and [26]} (Fig ...

2010

3.794

0.0

2013

3.941

0.0

2014

1.857

0.0

... To confirm the above thinking, dynamic atomic force microscopy (DAFM) was recently used to probe the surface of the metallic-glass thin films (MGTFs)^{[26], [29] and [30]} ...

... While the DAFM is a useful technique, however, it usually demands an atomic-scale surface smoothness^{[26] and [29]}, hence limiting its application to bulk metallic glasses (BMGs) ...

2011

7.943

0.0

... To confirm the above thinking, dynamic atomic force microscopy (DAFM) was recently used to probe the surface of the metallic-glass thin films (MGTFs)^{[26], [29] and [30]} ...

2012

3.794

0.0

... The former case corresponds to an ‘ideal’ or ‘perfect’ glass without the liquid-like atoms ^[31], while the latter to a ‘pure’ liquid without any solid-like atoms ...

1982

0.0

... 4(d), the loading curve can be derived from the Hertzian solution using the integral transform method ^[32]: ...

2011

35.749

0.0

... Again, this distribution is expected and agrees with the previous findings with respect to the distribution of local properties in MGs ^{[20] and [33]} ...

2010

35.749

0.0

... ^[34], glass transition can be viewed as a percolation process in which the slowly relaxing atoms, which corresponds to a large viscosity and a long relaxation time t_L, percolate to form the ‘skeleton’ of the glass whilst the rapidly relaxing atoms, which corresponds to a low viscosity and a short relaxation time t_s (t_L), are therefore left as the ‘residual liquidity’ embedded in the glass ...

2010

7.943

0.0

... ^[35], the viscosity and relaxation time of the solid-like regions could be even higher at a smaller stress ...