Characteristics of Twin Lamellar Structure in Magnesium Alloy during Room Temperature Dynamic Plastic Deformation

Cite this Article

Lou Chao, Zhang Xiyan, Duan Gaolin, Tu Jian, Liu Qing. Characteristics of Twin Lamellar Structure in Magnesium Alloy during Room Temperature Dynamic Plastic Deformation. Journal of Materials Science & Technology, 2014, 30(1): 41-46 Copy to clipboard

Permissions

Characteristics of Twin Lamellar Structure in Magnesium Alloy during Room Temperature Dynamic Plastic Deformation

Lou Chao, Zhang Xiyan^*, Duan Gaolin, Tu Jian, Liu Qing

School of Materials Science and Engineering, Chongqing University, Chongqing 400030, China

Corresponding author. Prof., Ph.D.; Tel./Fax: +86 23 65112154.

Abstract

The microstructures of the as-rolled magnesium alloy subjected to dynamic plastic deformation along the rolling direction have been investigated. Mostly one ${10 \bar{1} 2}$ twin variant or a twin variant pair is activated in a grain, leading to a parallel ${10 \bar{1} 2}$ twin lamellar structure. At the stage of twinning-dominated deformation (ε < ∼8%), lamellar thickness decreases significantly with strain, from 5.55 to 2.49 μm. The evolution of lamellar thickness during deformation is directly related to ${10 \bar{1} 2}$ twin activity. When plastic strain is greater than ∼8%, the twin lamellar structure disappears because the volume fraction of twins almost saturates at a value of ∼90%.

Keyword: Magnesium alloy;

{10 \bar{1} 2}

twin lamella; Lamellar thickness; Strain

Show Figures

1. Introduction

Deformation twinning plays an important role in the deformation of hexagonal close-packed (hcp) metals because of their limited slip systems^{[1], [2], [3] and [4]}. Due to the complicated interaction between twinning and slip, deformation twinning can effectively strengthen or weaken the strength and ductility of hcp metals ^[3]. For pure Mg and Mg alloys, which have the low stacking fault energy, twinning plays an important role during deformation, particularly at low temperatures and high strain rates^{[5] and [6]}. Generally three types of twins can be activated in magnesium alloys: ${10 \bar{1} 2}$ extension twins, compression twins on the ${10 \bar{1} 1}$ and ${10 \bar{1} 3}$ planes, and double twins, including ${10 \bar{1} 1} - {10 \bar{1} 2}$ and ${10 \bar{1} 3} - {10 \bar{1} 2}$ double twins^{[7], [8] and [9]}. ${10 \bar{1} 2}$ twinning is thought to be activated more frequently in several types of twins of Mg alloys. Due to the polar characteristic of ${10 \bar{1} 2}$ twinning, the deformation texture attributable to twinning always forms in wrought magnesium and magnesium alloys and results in high asymmetry and anisotropy in the mechanical properties of metals^{[10] and [11]}. Moreover, the twin boundaries acted as effective barriers for slip also play an important role in the deformation mechanisms of hcp materials^{[5], [12] and [13]}. Song and Li ^[14] investigated the effect of twin spacing on the deformation behavior of nano-twinned magnesium using molecular dynamics simulation and found that there is a pronounced shift in its mechanical behavior when twin spacing is smaller than 2.9 nm. Therefore, it is crucial to understand the twinning behavior in hcp materials, for microstructural design and applications. For a face-centered cubic (fcc) polycrystalline Cu subjected to a dynamic plastic deformation, twin boundary spacing decreases from 48 to 14 nm with increasing strain and steps into saturated state when deformation strain is greater than 1.2 ^[15]. When a nickel-base HASTELLOY C-2000 alloy was subjected to a surface severe plastic deformation treatment, the twin spacing decreased as the position became closer to the impacted surface ^[16]. However, a little has been reported so far on hcp metals. For the Mg alloys of hcp crystal structure, the development of the microstructural morphology caused by ${10 \bar{1} 2}$ twins is also closely related to plastic strain. Hence, it is of great interest to investigate the microstructural evolution of Mg alloys during deformation. ${10 \bar{1} 2}$ twin nucleation and propagation can be dramatically enhanced at dynamic rates, and contraction and secondary twinning are not favored ^[17]. So to facilitate twinning, dynamic plastic deformation (DPD) was employed to deform samples to several strains in this study.

2. Experimental

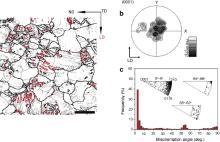
The hot-rolled AZ31 Mg alloy sheet (Mg–3%Al–1%Zn, wt%) has twin-free equiaxed grain structure ( Fig. 1(a)) and an average grain size of 34 μm calculated by the linear intercept method. As generally observed in annealed AZ31 sheets, the basal {0001} planes of this sheet were aligned almost parallel to the rolling plane, as shown in Fig. 1(b). Cylinders (8 mm in diameter and 12 mm in height) were cut from this sheet along the rolling direction (RD) ( Fig. 2). Samples were subjected to DPD just once with Instron Dynatup 8120 testing machine at room temperature and the strain rate is about 10³ s^-1. The deformation strain was defined as ε = ln( L₀/ L_d), where L₀ and L_d are the initial and final height of the samples, respectively. The initial texture was measured by X-ray diffraction in a Rigaku D/max-2500 PC. Scanning electron microscopy–electron back-scattered diffraction (SEM–EBSD) was utilized to analyze the microstructure and texture of samples after deformation. The deformation within the samples under uniaxial compression was of inhomogeneity, so EBSD data was acquired from the center of the cross section ( i.e. the ND–RD plane) of the impacted sample. EBSD scans were performed by FEI Nova400 FEG–SEM on the unit for 300 × 300 with a step size of 1 μm and EBSD information was acquired with Channel 5 software. The specimens for EBSD were prepared by standard metallographic polishing, then electropolished by using the commercial AC 2 electrolyte for 60 s at 20 V and 20 °C.

	Figure Option View Download New Window
	Fig. 1. Microstructural characteristics of the as-rolled material: (a) EBSD map, (b) (0001) pole figure.

	Figure Option View Download New Window
	Fig. 2. Schematic illustration of the sample orientations used for DPD testing. RD, TD and ND represent the rolling direction, the transverse direction and the normal direction, respectively; the arrows indicate the loading direction.

3. Results and Discussion

3.1. Microstructural evolution

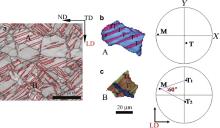
Fig. 3 shows the optical micrographs of DPD samples observed in the longitudinal section with different strain levels and the texture evolution during deformation. Only ${10 \bar{1} 2}$ twin is generated in grains during deformation. At the early stage of deformation, a lot of ${10 \bar{1} 2}$ twins are activated and the twin morphologies developed in a grain are almost parallel to each other, as shown in Fig. 3(a) and (b). With further strain, irregular twin shapes are obtained due to the coalescence of growing twins, as shown in Fig. 3(c) and (d). For compression perpendicular to the c-axis in the hcp crystal structure, the c-axis of the twinned region is oriented toward the loading direction (LD). The difference of twin textures with different strains ( Fig. 3) can be interpreted based on the different volume fractions of twins. For strain ε > ∼8%, the as-rolled texture with the c-axis aligned parallel to the normal direction (ND) is transferred to the twin texture with the c-axis aligned parallel to the RD ( Fig. 3(d)).

	Figure Option View Download New Window
	Fig. 3. EBSD maps and (0001) pole figures of AZ31 samples with different strains: (a) ε = 2.1%, (b) ε = 4.3%, (c) ε = 6.5%, (d) ε = 8.3%. LD represents loading direction.

3.2. Characteristic of

{10 \bar{1} 2}

twin lamellar structure

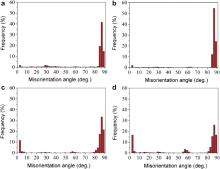
Theoretically, a grain could twin on six equivalent ${10 \bar{1} 2}$ twinning planes with one shear direction of $〈 10 \bar{1} 1 〉$ , but the selection of twin variants depends on the strain path^{[18] and [19]}. Fig. 4 shows the misorientation angle distributions of AZ31 samples with different strains. As shown in Fig. 4(a), a local peak at 80°–90° increases rapidly with increasing strain to ∼4% ( Fig. 4(b)) due to ${10 \bar{1} 2}$ twin nucleation, and then decreased as the interaction of growing twins ( Fig. 4(c) and (d)). For Mg alloys, several misorientation relationships can be generated between two ${10 \bar{1} 2}$ twin variants, i.e. 0° or 7.4° $〈 \bar{1} 2 \bar{1} 0 〉$ relationship between same twin variant pairs, and 60° $〈 10 \bar{1} 0 〉$ or 60.4° $〈 8 \bar{1} \bar{7} 0 〉$ relationship between different twin variant pairs^{[17] and [19]}. But the misorientations for the latter two are so close that it is hard to distinguish in EBSD map ^[20]. For compression perpendicular to the c-axis, most grains included just one ${10 \bar{1} 2}$ twin variant or a twin variant pair, so these twin bands were almost parallel to each other, such as grain A in Fig. 5(a), and orientations of grain matrix and the activated ${10 \bar{1} 2}$ variants are illustrated in Fig. 5(b). So a local peak at 80°–90° decreases as the intersection or coalescence of twins with further strain, and a misorientation relationship about 7.4° $〈 \bar{1} 2 \bar{1} 0 〉$ is generated, leading to a rapid increase in the peak of low misorientation angles about 0°–10° ( Fig. 4). As listed in , some grains generate different ${10 \bar{1} 2}$ twin variants, such as grain B in Fig. 5(a), and its orientation is illustrated in Fig. 5(c). So a local peak at ∼60° increases slightly with strain. In addition, a local peak at low angles (<5°) results from the dislocation pileups developing at the twin boundaries and the sessile dislocations within twins. It should be pointed out that the similar twin lamellar structure in our experiments has also been gotten by quasi-static compression (QSC), in which the loading direction is perpendicular to the c-axis of crystal lattice^{[19] and [20]}.

	Figure Option View Download New Window
	Fig. 4. Misorientation angle distributions of AZ31 samples with different strains: (a) ε = 2.1%, (b) ε = 4.3%, (c) ε = 6.5%, (d) ε = 8.3%. The rotation axis distributions in the crystal coordinate system indicate the different misorientation relationships.

	Figure Option View Download New Window
	Fig. 5. (a) Microstructure of DPD sample with ε = 4.3%, red lines indicate ${10 \bar{1} 2}$ twin boundaries; sketch maps (b) and (c) show grain A and B in (a) and their crystallographic orientations, respectively, M represents grain matrix, T, T1 and T2 represent activated ${10 \bar{1} 2}$ twin variants.

Table 1. Statistical results of the number of twinned grains

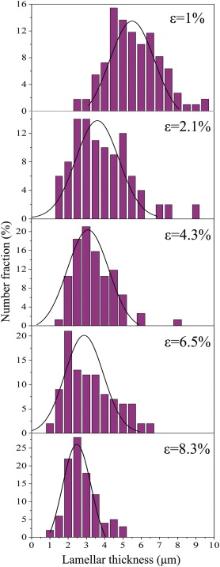
3.3. Evolution of lamellar structure

Lamellar thickness was measured by an average linear intercept with the aim of analyzing the relationship between the microstructural morphology and plastic strain. To ensure statistical validity, a large number of twinned grains have been investigated in five samples, corresponding to different strain levels of 1%, 2.1%, 4.3%, 6.5% and 8.3%, respectively, as listed in . Nearly all grains generate ${10 \bar{1} 2}$ twins in the statistical results, and a few grains do not form twins because grain orientations have a large deviation from ideal orientation of basal texture. The statistical results of lamellar thickness are presented in Fig. 6. The average lamellar thickness decreases from 5.55 μm at ε = 1% to 2.49 μm at ε = 8.3%. Meanwhile, the distribution range of lamellar thickness shrinks from 2–10.2 μm at ε = 1% to 1–4.85 μm at ε = 8.3%. Lamellar thickness decreases significantly with increasing strain.

	Figure Option View Download New Window
	Fig. 6. Statistical results of lamellar thickness with different strains.

3.4. Effect of plastic strain on the lamellar thickness

Fig. 7(a) shows the average lamellar thickness with different strains. It is obvious that lamellar thickness decreases with increasing strain to ∼8%. But the contribution of twinning to the deformation rapidly decreases with increasing strain because the capacity for twinning is exhausted locally within grains ( Fig. 7(b)). When plastic strain exceeds ∼8%, twin morphologies become irregular and the amount of twin boundaries finally decreases as twin-to-twin interactions causes a change in the misorientation angles of twin boundaries. As shown in Fig. 8, a few twin lamellae are found in the sample with ε = 11.4% ( Fig. 8(a) and (c)), and the initial texture with the c-axis aligned parallel to the ND is transferred to the twin texture with the c-axis aligned parallel to the RD ( Fig. 8(b)). As mentioned above, with increasing strain, a lot of 7.4° $〈 \bar{1} 2 \bar{1} 0 〉$ boundaries parallel to each other are generated (gray lines as shown in Fig. 8(a)), making it look like lamellar structure. A few ${10 \bar{1} 1}$ compression twins are activated in the twin area because c-axis aligns parallel to the loading direction, and the misorientation relationship of 56° $〈 1 \bar{2} 10 〉$ leads to the increase in the local peak at 50°–57° ( Fig. 8(c)).

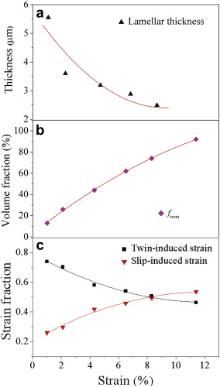	Figure Option View Download New Window
	Fig. 7. Microstructural statistical results: (a) lamellar thickness, (b) twin volume fraction f_twin, (c) twin/slip-induced strain rate of DPD AZ31 alloys with different strains.

Figure Option
View Download New Window

Fig. 8. (a) EBSD map of ε = 11.4% deformed sample,

{10 \bar{1} 2}

twin boundaries, grain boundaries and other boundaries with misorientation below 10° are indicated as red, black and gray lines, respectively; (b) (0001) pole figures; (c) misorientation angle distributions, and the rotation axis distributions in the crystal coordinate system indicate the different misorientation relationships.

The strain accommodated by twinning can be calculated as follows ^[18]:

When twinning dominated the deformation of AZ31 alloy, a large number of twin lamellae were generated in grains due to the parallel twin structure, and lamellar thickness decreased with increasing plastic strain. Obviously, this microstructural evolution is directly related to ${10 \bar{1} 2}$ twin nucleation and growth. Generally lamellar thickness decreases with the increase in the number of twin nucleation, or increases due to the growth of activated twins. A much higher stress is required for twin nucleation compared with twin growth ^[18]. So twin nucleation becomes more difficult, and the activated ${10 \bar{1} 2}$ twins are easier to develop with further strain. At the early stage of twinning-dominated deformation ( ε < ∼4%), a lot of twins are activated, leading to a rapid decrease of the lamellar thickness with increasing strain. And the twin nucleation per grain is associated with grain area ^[23]. The growth of activated twins led to the decrease in the initial grain area, so the nucleation of new twins became more difficult with further strain. Meanwhile, the coalescence of growing twins led to the decrease in lamellar numbers. When deformation strain exceeds ∼4%, a little change of lamellar thickness with strain can be attributed to the fact that twin nucleation was restrained. Capolungo et al. ^[24] thought that ${10 \bar{1} 2}$ twin thickening proceeded independently of slip in Mg. Here, it was thought that the twin growth would not be affected by dislocation slips.

Dislocation slips, replacing twinning, dominated the later deformation above ∼8%. The twin lamellar structure disappeared because the volume fraction of twins almost saturated at a value of ∼90%.

4. Conclusion

When the as-rolled AZ31 Mg alloy is subjected to dynamic plastic deformation perpendicular to the c-axis of hcp lattice, mostly one ${10 \bar{1} 2}$ twin variant or a twin variant pair is activated in a grain, leading to a parallel ${10 \bar{1} 2}$ twin lamellar structure. At the stage of twinning-dominated deformation ( ε < ∼8%), lamellar thickness decreases from 5.55 to 2.49 μm with increasing strain. The evolution of lamellar thickness during deformation is directly related to ${10 \bar{1} 2}$ twin activity. At low strains ( ε < ∼4%), the positive nucleation of twins results in a rapid decrease in the lamellar thickness. When plastic strain is greater than ∼4%, the twin nucleation which is restrained due to the limited grain area and the growth of activated twins lead to a gradual decrease in the lamellar thickness. Dislocation slips dominate the later deformation beyond ∼8%. At this stage, twin lamellar structure disappears because the volume fraction of twins almost saturates at a value of ∼90%.

Acknowledgements Acknowledgments

This work was supported by National Natural Science Foundation of China (Nos. , and ) and the Fundamental Research Funds for the Central Universities (No. ).

The authors have declared that no competing interests exist.

Reference

View Option

1.	M. R. Barnett, Mater. Sci. Eng. A, 464 (2007), pp. 1–7 [Cited within: 1]
2.	M. R. Barnett, Mater. Sci. Eng. A, 464 (2007), pp. 8–16 [Cited within: 1]
3.	M. H. Yoo, Mater. Trans. A, 12 (1981), pp. 409–418 [Cited within: 2] [JCR: 1.627]
4.	M. Shamsi, M. Sanjari, A. Z. Hanzaki, J. Mater. Sci. Technol. , 25 (2009), pp. 1039–1045 [Cited within: 1] [JCR: 1.198] [CJCR: 0.293]
5.	L. Jiang, J. J. Jonas, R. K. Mishra, A. A. Luo, A. K. Sachdev, S. Godet, Acta Mater. , 55 (2007), pp. 3899–3910 [Cited within: 2] [JCR: 3.941]
6.	J. W. Christian, S. Mahajan, Prog. Mater. Sci. , 39 (1995), pp. 1–157 [Cited within: 1] [JCR: 23.194]
7.	B. C. Wonsiewicz, W. A. Backofen, Trans. Metall. Soc. AIME, 239 (1967), pp. 1422–1431 [Cited within: 1]
8.	M. R. Barnett, Z. Keshavarz, A. G. Beer, X. Ma, Acta Mater. , 56 (2008), pp. 5–15 [Cited within: 1] [JCR: 3.941]
9.	P. Cizek, M. R. Barnett, Scripta Mater. , 59 (2008), pp. 959–962 [Cited within: 1] [JCR: 2.821]
10.	S. Kleiner, P. J. Uggowitzer, Mater. Sci. Eng. A, 379 (2004), pp. 258–263 [Cited within: 1]
11.	J. A. del Valle, F. Carreno, O. A. Ruano, Acta Mater. , 54 (2006), pp. 4247–4259 [Cited within: 1] [JCR: 3.941]
12.	E. W. Kelley, W. F. Hosford, Trans. Metall. Soc. AIME, 242 (1968), pp. 654–660 [Cited within: 1]
13.	L. E. Murr, E. Moin, F. Greulich, Scripta Metall. Mater. , 12 (1978), pp. 1031–1035 [Cited within: 1]
14.	H. Y. Song, Y. L. Li, Phys. Lett. A, 376 (2012), pp. 529–533 [Cited within: 1] [JCR: 1.11]
15.	G. H. Xiao, N. R. Tao, K. Lu, Mater. Sci. Eng. A, 513–514 (2009), pp. 13–21 [Cited within: 1]
16.	L. L. Shaw, A. L. Ortiz, J. C. Villegas, Scripta Mater. , 58 (2008), pp. 951–954 [Cited within: 1] [JCR: 2.821]
17.	N. V. Dudamell, I. Ulacia, F. Gálvez, S. Yi, J. Bohlen, D. Letzig, I. Hurtado, M. T. Perez-Prado, Acta Mater. , 59 (2011), pp. 6949–6962 [Cited within: 2] [JCR: 3.941]
18.	S. G. Hong, S. H. Park, C. S. Lee, Acta Mater. , 58 (2010), pp. 5873–5885 [Cited within: 3] [JCR: 3.941]
19.	S. G. Hong, S. H. Park, C. S. Lee, Scripta Mater. , 64 (2011), pp. 145–148 [Cited within: 3] [JCR: 2.821]
20.	M. D. Nave, M. R. Barnett, Scripta Mater. , 51 (2004), pp. 881–885 [Cited within: 2] [JCR: 2.821]
21.	M. A. Meyers, O. Vohringer, V. A. Lubarda, Acta Mater. , 49 (2001), pp. 4025–4039 [Cited within: 1] [JCR: 3.941]
22.	A. A. Salem, S. R. Kalidindi, R. D. Doherty, S. L. Semiatin, Metall. Mater. Trans. A, 37 (2006), pp. 259–268 [Cited within: 1] [JCR: 1.627]
23.	L. Capolungo, P. E. Marshall, R. J. McCabe, I. J. Beyerlein, C. N. Tome, Acta Mater. , 57 (2009), pp. 6047–6056 [Cited within: 1] [JCR: 3.941]
24.	L. Capolungo, I. J. Beyerlein, C. N. Tome, Scripta Mater. , 60 (2009), pp. 32–35 [Cited within: 1] [JCR: 2.821]

2007

0.0

... IntroductionDeformation twinning plays an important role in the deformation of hexagonal close-packed (hcp) metals because of their limited slip systems^{[1], [2], [3] and [4]} ...

2007

0.0

... IntroductionDeformation twinning plays an important role in the deformation of hexagonal close-packed (hcp) metals because of their limited slip systems^{[1], [2], [3] and [4]} ...

1981

1.627

0.0

... IntroductionDeformation twinning plays an important role in the deformation of hexagonal close-packed (hcp) metals because of their limited slip systems^{[1], [2], [3] and [4]} ...

... Due to the complicated interaction between twinning and slip, deformation twinning can effectively strengthen or weaken the strength and ductility of hcp metals ^[3] ...

2009

1.198

0.293

... IntroductionDeformation twinning plays an important role in the deformation of hexagonal close-packed (hcp) metals because of their limited slip systems^{[1], [2], [3] and [4]} ...

2007

3.941

0.0

Jiang

, J. J.

Jonas

, R. K.

Mishra

, A. A.

Luo

, A. K.

Sachdev

, S.

Godet

, Acta Mater. , 55 (2007), pp. 3899–3910

Abstract The evolution of twinning and texture in two Mg-based (+Al, Mn, Zn) alloys was investigated using uniaxial tension, uniaxial compression and ring hoop tension testing at temperatures from ambient to 250 °C and a strain rate of 0.1 s −1 . The results indicate that the initial extrusion texture plays an important role in the formation of different types of twins and that the twinning behavior also depends on the strain path. Contraction and double twinning are the dominant twinning mechanisms in uniaxial tension, while extension twinning prevails in uniaxial compression and ring hoop tension testing. Schmid factor analysis indicates that only components that are favorably oriented (i.e., with the highest SF values) can undergo rapid and complete twinning. The different twinning behaviors are shown to be responsible for the sharply contrasting strain hardening characteristics of the experimental flow curves and dramatic texture changes.

... For pure Mg and Mg alloys, which have the low stacking fault energy, twinning plays an important role during deformation, particularly at low temperatures and high strain rates^{[5] and [6]} ...

... Moreover, the twin boundaries acted as effective barriers for slip also play an important role in the deformation mechanisms of hcp materials^{[5], [12] and [13]} ...

1995

23.194

0.0

... For pure Mg and Mg alloys, which have the low stacking fault energy, twinning plays an important role during deformation, particularly at low temperatures and high strain rates^{[5] and [6]} ...

1967

0.0

... Generally three types of twins can be activated in magnesium alloys: {101¯2} extension twins, compression twins on the {101¯1} and {101¯3} planes, and double twins, including {101¯1}–{101¯2} and {101¯3}–{101¯2} double twins^{[7], [8] and [9]} ...

2008

3.941

0.0

M. R.

Barnett

, Z.

Keshavarz

, A. G.

Beer

, X.

, Acta Mater. , 56 (2008), pp. 5–15

Abstract The present work combines electron backscattering diffraction and Schmid analysis to investigate secondary twinning in the magnesium alloy Mg–3Al–1Zn. Inspection of the misorientations between the parent and doubly twinned volumes reveals that there are four possible variants. One of these variants (the one that forms a misorientation with the matrix characterized by 38° ) is favoured much more than the others. This variant involves the activation of secondary twinning systems quite inconsistent with Schmid-type behaviour. For the secondary twin to grow significantly it must take on a shape enforced by the primary twin. This is non-optimal for strain compatibility. It is argued that the 38° variant occurs most because it provides the closest match between the primary and secondary twinning planes, thus minimizing the compatibility strain.

2008

2.821

0.0

Cizek

, M. R.

Barnett

, Scripta Mater. , 59 (2008), pp. 959–962

Characteristics of the “contraction” twins, formed close to the fracture surface in Mg–3Al–1Zn alloy deformed in tension approximately perpendicular to the grain c -axes, are investigated using transmission electron microscopy. The grain c -axis contractions were largely accommodated by double-twins in a variant characterized by twin/matrix misorientation in conjunction with dislocation slip. A possible interpretation of the observed preference for this variant formation is given and some crystal plasticity modelling is performed to elucidate the matter.

2004

0.0

... Due to the polar characteristic of {101¯2} twinning, the deformation texture attributable to twinning always forms in wrought magnesium and magnesium alloys and results in high asymmetry and anisotropy in the mechanical properties of metals^{[10] and [11]} ...

2006

3.941

0.0

J. A.

del Valle

, F.

Carreno

, O. A.

Ruano

, Acta Mater. , 54 (2006), pp. 4247–4259

Abstract Equal channel angular pressing (ECAP) and large-strain hot rolling (LSHR) are widely used methods for refining the grain size in magnesium alloys. The hardening capability of the processed materials confers the resistance to develop tensile mechanical instabilities, therefore controlling ductility. In this work various magnesium alloys were processed using ECAP, LSHR and annealing treatments in order to control the texture and the grain size. Emphasis was laid upon the influence of these factors on work hardening behavior and dynamic recovery. In addition to the direct effect of texture through the change in the orientation factor for basal and prismatic slip, effects were found on dynamic recovery and the appearance of stage II of work hardening. The grain size refinement causes a strong decrease in the hardening rate. A contribution of grain boundary sliding to deformation gives a plausible explanation of these results.

1968

0.0

... Moreover, the twin boundaries acted as effective barriers for slip also play an important role in the deformation mechanisms of hcp materials^{[5], [12] and [13]} ...

1978

0.0

... Moreover, the twin boundaries acted as effective barriers for slip also play an important role in the deformation mechanisms of hcp materials^{[5], [12] and [13]} ...

2012

1.11

0.0

... Song and Li ^[14] investigated the effect of twin spacing on the deformation behavior of nano-twinned magnesium using molecular dynamics simulation and found that there is a pronounced shift in its mechanical behavior when twin spacing is smaller than 2 ...

0.0

... 2 ^[15] ...

2008

2.821

0.0

L. L.

Shaw

, A. L.

Ortiz

, J. C.

Villegas

, Scripta Mater. , 58 (2008), pp. 951–954

The Hall–Petch relationship in a nanotwinned alloy with absence of dislocation pile-ups is investigated for the first time. It is shown that, when the twin spacing is large ( d > 150 nm), the hardness exhibits a d −1/2 dependence. However, when the twin spacing is small ( d d −1 dependence results. These phenomena are interpreted based on dislocation-mediated mechanisms corroborated by the analysis of electron microscopy and X-ray diffractometry.

... When a nickel-base HASTELLOY C-2000 alloy was subjected to a surface severe plastic deformation treatment, the twin spacing decreased as the position became closer to the impacted surface ^[16] ...

2011

3.941

0.0

N. V.

Dudamell

, I.

Ulacia

, F.

Gálvez

, S.

, J.

Bohlen

, D.

Letzig

, I.

Hurtado

, M. T.

Perez-Prado

, Acta Mater. , 59 (2011), pp. 6949–6962

Abstract The microstructural evolution of an AZ31 rolled sheet during dynamic deformation at strain rates of ∼10 3 s −1 has been investigated by electron backscatter diffraction, X-ray and neutron diffraction. The influence of orientation on the predominant deformation mechanisms and on the recovery processes taking place during deformation has been systematically examined. The results have been compared with those corresponding to the same alloy tested quasi-statically under equivalent conditions. It has been found that strain rate enhances the activation of extension twinning dramatically, while contraction and secondary twinning are not significantly influenced. The polarity of extension twinning is even reversed in some grains under selected testing conditions. Significant grain subdivision by the formation of geometrically necessary boundaries (GNBs) takes place during both quasi-static and dynamic deformation of this AZ31 alloy. It is remarkable that GNBs of high misorientations form even at the highest strain rates. The phenomenon of recovery has been found to be orientation dependent.

... {101¯2} twin nucleation and propagation can be dramatically enhanced at dynamic rates, and contraction and secondary twinning are not favored ^[17] ...

... 4° 〈81¯7¯0〉 relationship between different twin variant pairs ^{[17] and [19]} ...

2010

3.941

0.0

S. G.

Hong

, S. H.

Park

, C. S.

Lee

, Acta Mater. , 58 (2010), pp. 5873–5885

Abstract The active twin variants during {10–12} twinning of magnesium alloys were dependent on the strain path (i.e., compression perpendicular to the c -axis or tension parallel to the c -axis), and their section mechanism was governed by the Schmid law. The activation of specific twin variants depending on the strain path induced a significant difference in twinning characteristics, such as twin morphology, volume fraction of twins with strain, and twin texture, and consequently gave rise to a totally different effect on the deformation. The differences in the deformation characteristics (flow stress and strain hardening) between both strain paths are explained in relation to activation stresses for twinning and slips, activities of twinning and slips in the deformation, the Hall–Petch effect by twinning-induced grain size change, and twinning-induced change in activities of slips.

... Characteristic of {101¯2} twin lamellar structure Theoretically, a grain could twin on six equivalent {101¯2} twinning planes with one shear direction of 〈101¯1〉, but the selection of twin variants depends on the strain path^{[18] and [19]} ...

... The strain accommodated by twinning can be calculated as follows ^[18]: ...

... A much higher stress is required for twin nucleation compared with twin growth ^[18] ...

2011

2.821

0.0

S. G.

Hong

, S. H.

Park

, C. S.

Lee

, Scripta Mater. , 64 (2011), pp. 145–148

The {1 0 −1 2} twinning activity in plastic deformation of a polycrystalline magnesium alloy was investigated using the in situ electron backscatter diffraction technique in combination with Schmid factor analysis. The activation of different twin variants depending on the strain path introduced a significant difference in the intersection characteristics between twin bands, causing a totally different twinning contribution to the deformation. The intersection between different twin variant pairs was found to retard the twin growth and promote the nucleation of new twins.

... 4° 〈81¯7¯0〉 relationship between different twin variant pairs ^{[17] and [19]} ...

... In addition, a local peak at low angles (c-axis of crystal lattice ^{[19] and [20]} ...

2004

2.821

0.0

M. D.

Nave

, M. R.

Barnett

, Scripta Mater. , 51 (2004), pp. 881–885

Abstract Microstructures of textured polycrystalline Mg samples compressed parallel and perpendicular to the predominant c -axis direction in a channel die are characterized using EBSD. Anomalous peaks in the misorientation angle distribution of the latter sample result from twinning on two different planes within individual grains.

... But the misorientations for the latter two are so close that it is hard to distinguish in EBSD map ^[20] ...

... In addition, a local peak at low angles (c-axis of crystal lattice ^{[19] and [20]} ...

2001

3.941

0.0

M. A.

Meyers

, O.

Vohringer

, V. A.

Lubarda

, Acta Mater. , 49 (2001), pp. 4025–4039

Abstract A constitutive approach is developed that predicts the critical stress for twinning as a function of external (temperature, strain rate) and internal (grain size, stacking-fault energy) parameters. Plastic deformation by slip and twinning are considered as competitive mechanisms. The twinning stress is equated to the slip stress based on the plastic flow by thermally assisted movement of dislocations over obstacles, which leads to successful prediction of the slip-twinning transition. The model is applied to body centered cubic, face centered cubic, and hexagonal metals and alloys: Fe, Cu, brasses, and Ti, respectively. A constitutive expression for the twinning stress in BCC metals is developed using dislocation emission from a source and the formation of pile-ups, as rate-controlling mechanism. Employing an Eshelby-type analysis, the critical size of twin nucleus and twinning stress are correlated to the twin-boundary energy, which is directly related to the stacking-fault energy (SFE) for FCC metals. The effects of grain size and SFE are examined and the results indicate that the grain-scale pile-ups are not the source of the stress concentrations giving rise to twinning in FCC metals. The constitutive description of the slip-twinning transition are incorporated into the Weertman–Ashby deformation mechanism maps, thereby enabling the introduction of a twinning domain. This is illustrated for titanium with a grain size of 100 μm.

2006

1.627

0.0

A. A.

Salem

, S. R.

Kalidindi

, R. D.

Doherty

, S. L.

Semiatin

, Metall. Mater. Trans. A, 37 (2006), pp. 259–268

Novel experiments were conducted to elucidate the effect of deformation twinning on the mechanical response of high-purity α-titanium deformed at room temperature. Orientation-imaging microscopy (OIM), microhardness, and nanohardness evaluations were employed in conjunction with optical microscopy and quasi-static compression testing to obtain insight into the deformation mechanisms. Hardness measurements revealed that the newly formed deformation twins were harder than the matrix. This observation is perhaps the first experimental evidence for the Basinski mechanism for hardening associated with twinning, arising from the transition of glissile dislocations to a sessile configuration upon the lattice reorientation by twinning shear. This work also provided direct evidence for two competing effects of deformation twinning on the overall stress-strain response: (1) hardening via both a reduction of the effective slip length (Hall-Petch effect) and an increase in the hardness of twinned regions (Basinski mechanism) and (2) softening due to the lattice reorientation of the twinned regions.

1.AFRL/MLLM Air Force Research Laboratory, Materials and Manufacturing Directorate Wright-Patterson AFB OH 2.Universal Technology Corporation Dayton OH 3.Drexel University the Department of Materials Science and Engineering Philadelphia PA 4.AFRL/MLLM Air Force Research Laboratory, Materials and Manufacturing Directorate USA

2009

3.941

0.0

Capolungo

, P. E.

Marshall

, R. J.

McCabe

, I. J.

Beyerlein

, C. N.

Tome

, Acta Mater. , 57 (2009), pp. 6047–6056

Abstract An in-depth statistical analysis using electron backscatter diffraction (EBSD) is carried out to expose statistical correlations between { } twinning and grain size, crystallographic orientation, grain boundary length, and neighbor misorientation in high-purity polycrystalline zirconium strained to 5% and 10% at 77 K. A strong correlation was found between the active twin variant and crystallographic orientation. The propensity of a grain to twin or not was found to be only weakly dependent on grain area and diameter. Within the population of grains containing twins the number of twins per grain noticeably increases with grain area, and twin thickness is found to be rather insensitive to grain size and orientation. A weak preference for twinning was found for smaller grain boundary misorientation angles. These and the other statistical results reported can improve theoretical treatments for twin nucleation in polycrystal models. The statistical methodology presented has general applicability for all twin types in a wide range of metals.

2009

2.821

0.0

Capolungo

, I. J.

Beyerlein

, C. N.

Tome

, Scripta Mater. , 60 (2009), pp. 32–35

We study two possible twin growth mechanisms in hexagonal close-packed (hcp) metals: a slip-assisted one, based on dislocation reactions at twin interfaces, and a slip-independent one, based on the direct activation of twin dislocations. A twin thickening rate law is developed to estimate the contribution of slip dislocations to twin growth in hcp crystals. Application of the model to Mg single crystals, and comparison with experimental data, suggests that twin thickening proceeds independently of slip.

... ^[24] thought that {101¯2} twin thickening proceeded independently of slip in Mg ...