1. Introduction
Elastic constants are fundamental material properties which reflect the nature of atomic binding on one hand and closely related to the mechanical properties such as hardness, tensile strength, fracture stress, etc., on the other hand [1]. Calculations of elastic constants have long been one of the main tasks and benchmark of first-principles methods based on density functional theory. Nowadays, elastic constants may be calculated very accurately by using first-principles method at 0 K (e.g., Ref. [2]). However, elastic constants are generally measured experimentally at finite temperature. This is one of the main sources of the error between theoretical and experimental elastic constants. Furthermore, the temperature dependence of the elastic constants may be crucial to the understanding of material behavior. For examples, for the materials undergoing structural martensitic transition (MT) upon changing temperature (e.g., TiNi [3]), the MT process is coupled with elastic constant hardening of the martensite and softening of the austinite with lowering temperature. The critical temperature for the MT is high pertinent to the temperature dependent elastic constants. In regard to the above aspects, accurate calculation of the elastic constants at finite temperature from first-principles is profound.
There are mainly two first-principles method based techniques for the calculations of elastic constants at finite temperature. The first one relies on the thermodynamic properties from static first-principles calculations in combination with the quasiharmonic approximation (QHA) or particle in a cell model [4]. The temperature dependent elastic constants were obtained by calculating the strain dependence of the free energy at the volume corresponding to a given temperature. The free energy is quasiharmonic, evaluated from the phonon dispersions of the strained lattice. This approach (denoted as QHA1 hereafter) has been used to calculate the temperature dependent elastic constants of MgO and MgSiO3 [5,6], W [7], Al [8], etc. Because the direct calculations of the phonon dispersions of random alloys are cumbersome, Vitos et al. developed another QHA scheme (denoted as QHA2 hereafter) to calculate the elastic constants of random alloys [9,10]. The contribution of the temperature effect to the elastic constants was separated into constant temperature and constant volume components. For the constant temperature component, the temperature induced variation of the elastic constant is evaluated as the difference between the one with volume V corresponding to a given temperature T and the one with equilibrium volume V0 at 0 K. The V(T) relationship is determined from the quasiharmonic Debye model. For the constant volume component, the free energy of the strained lattice is calculated with the contribution of electronic entropy at temperature T and volume V0. The electron-phonon coupling effect may also be included in the free energy by considering the effect of Lorentz-type smearing of the electronic density of states at finite temperature where empirical electron-phonon coupling constant λel-ph is adopted to evaluate the phonon limited electron life time [11,12].
Alternative to the QHA scheme, ab initio molecular dynamics (AIMD) method has also been applied to calculate the temperature dependent elastic constants. The stresses of the strained lattice are calculated by using AIMD at given temperature T and volume V(T). The elastic constants under temperature T are then obtained by fitting the stress-strain relationship. AIMD has been applied to calculate the elastic constants of CaSiO3 [13] and Fe [14] under Earth’s mantle core conditions. The elastic constants of TiN [15] have also been evaluated as function of temperature by using AIMD calculations. It is noted that these materials in question are generally “hard” with large elastic constants. The application of AIMD on the calculation of elastic constants of “soft" materials is not found in literature. The main reason could be that the stress of the strained lattice fluctuates against the time step. For the “soft” materials with small elastic constants, the amplitude of the stress fluctuation for a given strain is too large relative to the “true” value of the stress, leading to errors overriding the calculated elastic constants. This may not matter too much for “hard” materials because the elastic constants are large and the corresponding stress of the strained lattice is large such that the influence of the stress fluctuation is relatively insignificant.
In the present work, we explore the feasibility of AIMD in the calculations of the temperature dependent elastic constants of relatively “soft” material. We choose aluminum (Al) with face-centered cubic structure as an example. The experimental C11, C12 and C44 of Al are about 123 GPa, 65 GPa and 30 GPa, much lower that those of “hard” materials such as TiN with C11, C12 and C44 of 611 GPa, 130 GPa and 160 GPa, respectively [15]. For comparison, the QHA2 scheme is also adopted to calculate the temperature dependent elastic constants of Al. The paper is arranged as follows. The calculation details are given in Section 2. We report the results of temperature dependent volume and elastic constants in Section 3. The individual contributions of the volume expansion, lattice vibration, and electronic temperature to the temperature induced variation of elastic constants are discussed in this section. Finally, we conclude our work in Section 4.
2. Method
2.1. AIMD scheme
With the AIMD scheme, the elastic constants are calculated by linear fitting of the stress-strain relationship. Strain tensors are applied on the system with volume V(T) and then the corresponding stresses are calculated at temperature T by using AIMD. We choose the orthorhombic strain tensor
and monoclinic strain tensor
The orthorhombic strain (Eq. (1)) results in stress-strain relationship
whereas the monoclinic strain (Eq. (2)) leads to
For the thermal expansion V(T), we calculate the external pressure P(T) of 5 different volumes around the experimental equilibrium volume at given temperature T using AIMD. The equilibrium volume at each temperature T is then obtained by minimizing the external pressure P(T) against V(T) using the Birch-Murnaghan P-V equation of state [17].
2.2. QHA2 scheme
As introduced in Sec. 1, in the QHA2 scheme, the temperature dependent elastic constants are separated to constant temperature part, $\text{ }\!\!\Delta\!\!\text{ C}_{\text{ij}}^{\text{T}}\text{(T)}={{\text{C}}_{\text{ij}}}\text{ }\!\![\!\!\text{ }{{\text{T}}_{0}}\text{,V(T) }\!\!]\!\!\text{ }-{{\text{C}}_{\text{ij}}}\text{(}{{\text{T}}_{0}}\text{,}{{\text{V}}_{0}}\text{)}$, and constant volume part, $\text{ }\!\!\Delta\!\!\text{ C}_{\text{ij}}^{\text{V}}\text{(T)}={{\text{C}}_{\text{ij}}}\text{(T,}{{\text{V}}_{0}}\text{)}-{{\text{C}}_{\text{ij}}}\text{(}{{\text{T}}_{0}}\text{,}{{\text{V}}_{0}}\text{)}$. Here, Cij[T0,V(T)] is the static elastic constant (T0 = 0 K) calculated with volume at temperature T, V(T). Cij(T0,V0) is the static elastic constant for equilibrium volume V0=V(T0) at T0 = 0 K. Cij(T,V0) is the elastic constants calculated with equilibrium volume V0 with electronic temperature of T. The final elastic constants is obtained by ${{\text{C}}_{\text{ij}}}\text{(T)}={{\text{C}}_{\text{ij}}}\text{(}{{\text{T}}_{0}}\text{,}{{\text{V}}_{0}}\text{)+ }\!\!\Delta\!\!\text{ C}_{\text{ij}}^{\text{T}}\text{(T)+ }\!\!\Delta\!\!\text{ C}_{\text{ij}}^{\text{V}}\text{(T)}$. The constant temperature component takes care of the thermal expansion effect on the elastic constants whereas the constant volume component addresses mainly the electronic thermal excitation effect. For the constant volume part, we consider solely the contribution of the electronic entropy with the electron-phonon coupling effect neglected, and therefore, we change the notation from $\text{ }\!\!\Delta\!\!\text{ C}_{\text{ij}}^{\text{V}}\text{(T)}$ to $\text{ }\!\!\Delta\!\!\text{ C}_{\text{ij}}^{\text{e}}\text{(T)}$ hereafter.
The static first-principles calculations of elastic constants of cubic system may be much more convenient than the AIMD strategy. One may adopt only one strain tensor
and evaluate the elastic constants with
The strains ε may also be much smaller (e.g., one order of magnitude) than those for the AIMD calculations. However, in order to reduce the error induced by the different strain tensors and make the elastic constants from AIMD and QHA2 calculations comparable, we employ exactly the same strain tensors (i.e., Eqs. (1) and (2)) and strain magnitude to calculate the elastic constant in the QHA2 calculations.
For the constant temperature component, the elastic constants are calculated at different volume V(T) at temperature T. The thermal expansion V(T) is determined with quasiharmonic Debye model. The static total energies E(V) are calculated for 21 volumes V around the equilibrium volume V0. Then the V(T)~T relationship is obtained by fitting the E(V)-V data points with the thermal equation of state [18].
For the constant volume component, we consider only the electronic temperature that enters into DFT as the Fermi-Dirac electronic smearing parameter Σ (Σ = kBT with kB being the Boltzmann constant). The elastic constants C(T,V0) are calculated at various electronic temperature of T. The elastic constants at T = 0 (i.e., Σ = 0), C(0,V0), are obtained by extrapolating the C(T,V0)~T relationships to T = 0.
2.3. Calculation details
The calculations are carried out with the plane wave pseudopotential method implemented in the Vienna Ab Initio Simulation Package [[19], [20], [21]] (VASP). The projector-augmented wave [22,23] (PAW) potentials is adopted to describe the electron-core interaction. The generalized gradient approximation parameterized by Perdew, Burke, and Ernzerhof [24] is used for the electronic exchange-correlation functional. The plane-wave cut-off energy is set as 350 eV.
The size of the supercell for both the QHA2 and AIMD calculations is 3 × 3×3 of the FCC unit cell, containing 108 atoms. The k-point mesh for the irreducible Brillouin zone sampling is 4 × 4×4. For the QHA2 calculations, the energy tolerance for the electronic relaxation is set as 1 × 10-6 eV while the force tolerance for the ion relaxation is set as 0.01 eV/Å. The Born-Oppenheimer molecular dynamics is used for the AIMD calculations such that the electronic and ionic subsystems are fully decoupled [25]. The energy tolerance for the electronic relaxation is set as 1 × 10-5 eV. We use a canonical ensemble (NVT) to maintain the desired temperature for all the AIMD simulations. The Nosé algorithm [26] with mass parameter of 2 is used for the thermostat. The total number of time steps is 5000 with each time step corresponding to 2 fs. The calculations are performed from 10 K (near absolute zero) to 900 K (near melting point).
3. Results and discussion
3.1. Thermal expansion
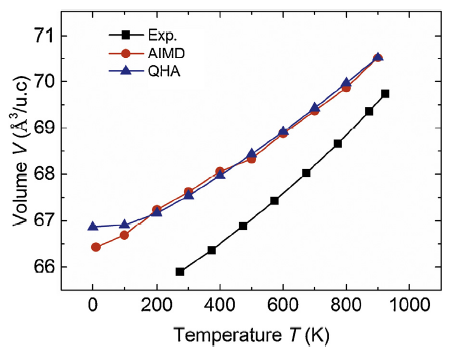
Both the AIMD and QHA2 schemes need the temperature dependent volume V(T). Fig. 1 shows the volumes of pure Al as functions of temperature T from AIMD and QHA Debye model calculations. As expected, the volume expands with increasing temperature. The V(T)~T curve from AIMD calculations is in perfect agreement with that from the QHA calculations above temperature of 200 K. The error between them below 200 K is also negligible. Therefore, we adopt the AIMD V(T) for both AIMD and QHA2 calculations in order to make the contributions from volume expansion exactly the same for both calculations. Displayed also in Fig. 1 is the volume from experimental measurements [27]. The theoretical volume is larger than the experimental values but with error no more than 2%, corresponding to lattice constant error of no more than 0.7%. The agreement between the theoretical and experimental volumes is slightly better at high temperature than at low temperature.
Fig. 1.
Fig. 1.
Volumes of pure Al as functions of temperature from ab initio molecular dynamics (AIMD, red circles) and quasiharmonic Debye model (QHA, blue triangles) calculations, in comparison with experimental measurements (black squares). The experimental data is from the high-temperature Debye-Scherrer X-ray measurements of Wilson [27].
3.2. Stress fluctuation and AIMD error evaluation
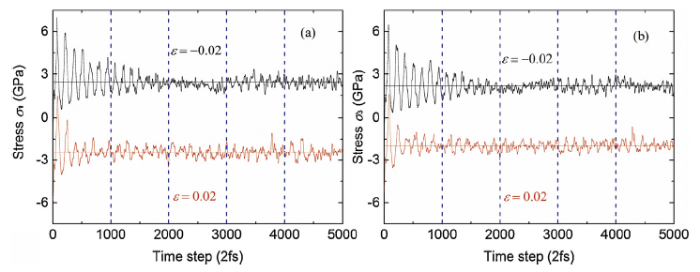
As introduced in Sec. 1, the stress of the strained lattice fluctuates against the time step during the AIMD calculations. As examples, we present the stresses σ1 and σ3 on Al supercell induced by orthorhombic strains ε0=-0.02 and 0.02 at 700 K to show the stress fluctuation (see Fig. 2). The stress σ1 averaged over the 5000 time steps is 2.44 GPa for ε0=-0.02 and -2.44 GPa for ε0 = 0.02. For σ3, the stresses are respectively 2.17 GPa and-1.97 GPa for ε0=-0.02 and ε0 = 0.02. The amplitudes of the fluctuations of σ1 and σ3 are about ±0.6 GPa for both strains after about 1500 time steps when the AIMD calculations are converged. In the present work, we take the stress averaged over the 5000 time steps to calculate all the elastic constants (solid circles in Fig. 3). The error associated with the stress fluctuation is evaluated with the converged amplitude of the fluctuation, which is shown as the thin error bars in Fig. 3. In order to evaluate the influence of the number of time steps on the calculated elastic constant, we present another kind of error for the AIMD calculations. The elastic constants are calculated with the stresses averaged over every 1000 time steps. The error between these elastic constants and the ones calculated with the stresses averaged over total 5000 time steps is then evaluated, shown in Fig. 3 as the thick error bars.
Fig. 2.
Fig. 2.
(Color online) Fluctuation of the stresses σ1 and σ3 on Al supercell induced by orthorhombic strains ε0=-0.02 and 0.02 and from ab initio molecular dynamic (AIMD) calculations at 700 K.
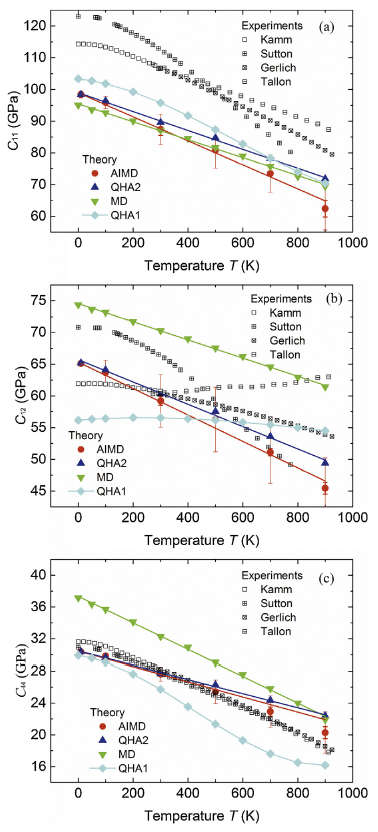
Fig. 3.
Fig. 3.
(Color online) Single crystal elastic constants of FCC Al as functions of temperature T from present AIMD (red circles) and QHA2 (blue upward triangles) as well as molecular dynamic (MD, green downward triangles) with empirical potentials and QHA1 (cyan diamonds) calculations by Pham et al. [8], in comparison with available experimental measurements (black squares) [[28], [29], [30], [31]]. The slashes are for the linear fitting of the calculated data points. The red thin vertical lines represent the stress fluctuation amplitude associated error bars from the AIMD calculations while the thick ones are for the time step associated error bars.
As seen in Fig. 3, the error determined with the amplitude of the stress fluctuation (thin error bars) is quite small at low temperature. In general, the stress fluctuation amplitude associated error increases monotonically with increasing temperature, except the error of C12 that remains almost constant for temperature above 500 K. The largest relative errors of C11, C12 and C44 are all about ±10%.
The error associated with the time steps (thick error bars in Fig. 3) is very small (no more than ±4%) for all the elastic constant components, indicating that the calculated elastic constants are not sensitive to the number of time steps. This means that we actually do not need to run too many AIMD steps to get elastic constants with reasonable accuracy, which may improve significantly the efficiency of the calculations. It is well known that AIMD calculations are expensive and time consuming. The insensitivity of the elastic constants on the number of time steps makes AIMD calculations of elastic constants more feasible.
3.3. Temperature dependent elastic constants
As seen from Fig. 3, the elastic constants C11, C12 and C44 decrease almost linearly with increasing temperature from both AIMD and QHA2 calculations. The elastic constant Cij from the present AIMD calculations decrease faster than those from the QHA2 calculations with increasing temperature T for all the elastic constant components. The reason is mainly that the contribution of the lattice vibration to the temperature dependent elastic constant is not considered in the present QHA2 calculations. We will discuss this point in more detail hereafter.
Pham et al. [8] have calculated the temperature dependent elastic constants of Al using QHA1 scheme and molecular dynamics (MD) simulation. C11 from the QHA1 and MD calculations are in general agreement with those from the AIMD and QHA2 calculations. The MD C12 is about 10-15 GPa higher than the AIMD and QHA2 C12s. The AIMD, QHA2 and MD yield apparent decreasing C12 with increasing temperature. However, the QHA1 C12 remains almost constant, which might be partly ascribed to the fact that the contribution of the lattice vibration to C12 was not correctly captured in the QHA1 calculations [8]. At the same temperature, the MD C44 is higher than the QHA1 C44 while AIMD and QHA2 C44s lie in between MD and QHA1 C44s. At very low temperature, the AIMD and QHA2 C44s are close to the QHA1 C44 whereas they approach to the MD C44 at high temperature. MD and QHA1 predicted faster decrease of C44 than AIMD and QHA2.
The experimental elastic constants of Al against temperature [[28], [29], [30], [31]] shown in Fig. 3 were all measured with the composite piezoelectric ultrasonic oscillator technique [32,33]. The only difference is that the wave frequencies used by Sutton [29] and Tallon and Wolfenden [31] were relative low (at KHz level) whereas those used by Kamm and Alers [28] and Gerlich and Fisher [30] were higher (at MHz level). It was believed that the low frequency measurement is less accurate because it is sensitive to the sample geometry and might be influenced by the dislocation motion [30]. As shown in Fig. 3, the elastic constants from experimental measurements are scattered except for C44. The temperature dependence of C11 and C12 varies for different experiment measurements as demonstrated by the different Cij~T slopes. Especially, the measurement of Tallon et al. even generated C12 increasing slightly with temperature T, in contrast to the trends measured by other experimentalists. Considering the scattering of the measured elastic constants, the theoretical elastic constants are in good agreement with those from experimental measurements. It is noted that the theoretical C11 and C12 are systematically smaller than those from experimental measurements, especially for C11. The reason is that the GGA-PBE exchange-correlation functional employed in the work is known to underestimate the atomic binding such that results in lower elastic constants.
3.4. Decomposed contributions of temperature to elastic constants
From the QHA calculations of the temperature dependent elastic constants, we get to know that the contribution to the elastic constants may separated mainly into three parts: volume expansion, lattice vibration [34], and electronic temperature, with the electron-phonon coupling neglected. QHA1 includes volume expansion and lattice vibration contributions while QHA2 considers volume expansion and electronic temperature effects. It is very interesting to know how much the three parts contribute individually to the temperature dependent elastic constants.
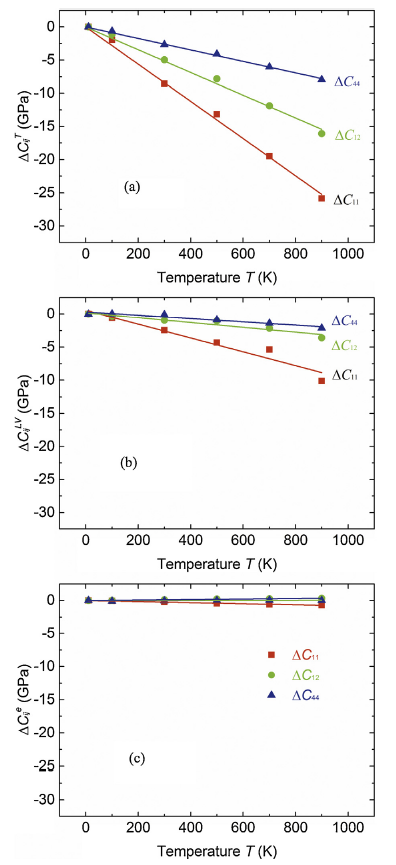
The elastic constants calculated with AIMD include the volume expansion and lattice vibration contributions, similar to the case of QHA1. The total contribution of the temperature to the elastic constants is $\text{ }\!\!\Delta\!\!\text{ }{{\text{C}}_{\text{ij}}}\left( \text{T} \right)={{\text{C}}_{\text{ij}}}\left( \text{T,V} \right)-{{\text{C}}_{\text{ij}}}\text{(}{{\text{T}}_{0}}\text{,}{{\text{V}}_{0}}\text{)}$. The contribution of the lattice vibration may be extracted as $\text{ }\!\!\Delta\!\!\text{ C}_{\text{ij}}^{\text{LV}}\left( \text{T} \right)=\text{ }\!\!\Delta\!\!\text{ }{{\text{C}}_{\text{ij}}}\left( \text{T} \right)-\text{ }\!\!\Delta\!\!\text{ C}_{\text{ij}}^{\text{T}}\text{(T)}$ with ΔCij(T) from the AIMD calculations. The contributions of volume expansion and electronic entropy are respectively $\text{ }\!\!\Delta\!\!\text{ C}_{\text{ij}}^{\text{T}}\text{(T)}$ and $\text{ }\!\!\Delta\!\!\text{ C}_{\text{ij}}^{\text{e}}\text{(T)}$ as detailed in Section 2.2. Fig. 4 displays the decomposed contributions of temperature to the elastic constants of Al.
Fig. 4.
Fig. 4.
(Color online) Decomposed contributions of the temperature to the elastic constants: (a) the volume expansion effect; (b) the lattice vibration effect; (c) the electronic temperature effect. The slashes are for the linear fitting of calculated data points. For the convenience of intuitive comparison, we set the same y-scale for all elastic constant components.
As seen in Fig. 4(a), the volume expansion contributes the major part of the temperature dependent elastic constants. At temperature of 900 K, the volume expansion induced elastic constants reduction $\text{ }\!\!\Delta\!\!\text{ C}_{\text{ij}}^{\text{T}}\text{(T)}$ are respectively -26 GPa, -16 GPa and-8 GPa for C11, C12 and C44 (see Fig. 4(a), which are about 75~80% of the total amount of the temperature induced variation of the elastic constants.
The contribution of the lattice vibration, which softens the elastic constants as well, is minor (Fig. 4(b)). The reduction of the elastic constants induced by the lattice vibration, $\text{ }\!\!\Delta\!\!\text{ C}_{\text{ij}}^{\text{LV}}\text{(T)}$, are respectively about -10 GPa, -4 GPa and-2 GPa for C11, C12 and C44 at temperature of 900 K (Fig. 4b), about 20~25% of the total amount. The contribution of lattice vibration to the temperature dependent elastic constants of Al has also been evaluated by Pham et al. [8] using QHA1 scheme. The vibrational contribution $\text{ }\!\!\Delta\!\!\text{ C}_{\text{ij}}^{\text{LV}}\text{(T)}$ was predicted to reduce C11 by about 10 GPa, in perfect agreement with our AIMD calculations. However, C12 was incorrectly predicted to be hardened by the lattice vibration [8], which was ascribed to the small supercell size used in the calculations. In general, the elastic constants of materials with dynamically stable crystal structure should be softened by lattice vibration. Of course, the situation will be opposite for the materials (e.g., high temperature austenite phases during martensitic transition) stabilized by thermal effect, for which the lattice vibration hardens the elastic constants with increasing temperature [11,12].
The contribution of the electronic entropy is negligible for all elastic constant components (Fig. 4c). $\text{ }\!\!\Delta\!\!\text{ C}_{\text{ij}}^{\text{e}}\text{(T)}$ does not always decrease with increasing temperature. $\text{ }\!\!\Delta\!\!\text{ C}_{11}^{\text{e}}\text{(T)}$ decreases slightly (-0.68 GPa at 900 K) while $\text{ }\!\!\Delta\!\!\text{ C}_{12}^{\text{e}}\text{(T)}$ increases slightly (0.32 GPa at 900 K) with temperature. $\text{ }\!\!\Delta\!\!\text{ C}_{44}^{\text{e}}\text{(T)}$ is one magnitude smaller. The influence of the electronic temperature on the elastic constant is determined by the shape of the electronic density of states (DOS) and its response to the strain applied on the crystal lattice. $\text{ }\!\!\Delta\!\!\text{ C}_{\text{ij}}^{\text{e}}\text{(T)}$ can be negative or positive depending on the DOS and the applied strain tensor [9].
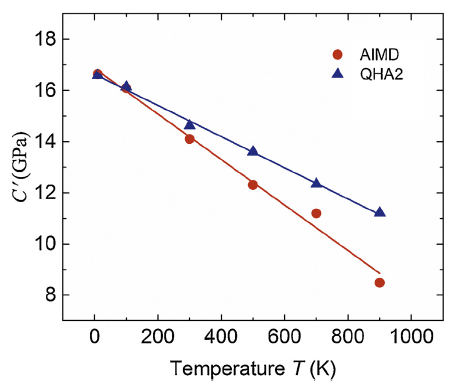
3.5. Elastic stability
As a cubic crystal, the elastic constants of Al should follow the Born stability criteria [35], i.e., C11-C12>0, C11+2C12>0, and C44>0. Fig. 5 shows tetragonal shear modulus $\text{C }\!\!'\!\!\text{ }=\frac{1}{2}\text{(}{{\text{C}}_{11}}-{{\text{C}}_{12}}\text{)}$ against the temperature T. As seen in figure, C' decreases with increasing temperature but remains positive with temperature up to 900 K. This is also the case for C11+2C12 and C44 as shown in Fig. 3. Therefore, although the elastic stability of Al is weakened by the raising temperature, the elastic stability requirements are satisfied for temperature up to 900 K. This is one of the reasons why FCC Al does not undergo structure transition before melting, noting that the melting point of Al is about 933 K [36]. AIMD predicts faster decreasing of C' (Fig. 5), C11+2C12 and C44 (Fig. 3) than QHA2 does, indicating that the lattice vibration destabilizes elastically FCC Al with increasing temperature because the lattice vibration is responsible for the difference between the elastic constants from AIMD and QHA2 calculations as discussed in Section 3.4.
Fig. 5.
Fig. 5.
(Color online) Shear modulus C' of FCC Al as functions of temperature T from the AIMD (red circles) and QHA2 (blue upward triangles). The slashes are for the linear fitting of calculated data points.
4. Conclusions
In the present work, the temperature dependent single crystal elastic constants of FCC Al were calculated by using both ab initio molecular dynamics (AIMD) and static first-principles method with quasiharmonic approximation (QHA2). The main results are summarized as follows.
(1) By choosing proper strain tensors and magnitude of the strain, the elastic constants of relatively “soft” metal Al may be calculated reliably by using AIMD. The elastic constants from AIMD calculations are not sensitive to the number of time steps, which ensure an efficient calculation of the temperature dependent elastic constants.
(2) The elastic constants from both AIMD and QHA2 calculations decrease almost linearly with raising temperature, in good agreement with experimental measurements.
(3) For FCC Al, the volume expansion effect contributes the major part in the temperature induced variation of the elastic constants, the contribution of lattice vibration is minor, while the electronic temperature effect is negligible. Both the volume expansion and lattice vibration soften the elastic constants. We would like to emphasize here that this trend might not hold for the thermally stabilized crystals.
(4) Although the elastic constants soften with increasing temperature, FCC Al satisfies the Born elastic stability criteria with temperature up to the experimental melting point. This is why there is no temperature driving structure transition for Al.
Acknowledgements
The authors are grateful to the National Key Research and Development Program of China (No. 2016YFB0701301), the National Nature Science Foundation of China (No. 91860107), and the National Key Basic Research Program (No. 2014CB644001) for financial supports.
Reference




 WeChat
WeChat