The PVT behavior of compounds is attributed to the changing of specific volume (1/density) with changes in temperature and pressure. This behavior in injection molding simulation is an integral know-how to determine the compressibility of the thermoplastic injection polymer compound. The amount of shrinkage in injection molded polymer compound can be considered as a direct function of the PVT behavior. The two-domain Tait PVT model, which consists of thirteen coefficients, is required to be data fitted, where V (m³/kg) is specific volume, T (K) temperature, T_t (K) transition temperature and P (Pa) is pressure. The b_1m tob_4m, b_1s to b_4s, and b₅ to b₉ are coefficients.

VT, P=V0t1-0.0894×ln⁡ln1+PBT+VtT, P(1)

when T> T_t​, V_t  (T,  P)=0 (2)

V₀=b_1m+b_2m  (T-b₅), B(T)=b_3mexp[-b_4m  (T-b₅)]

when T< T_t(3)

V0=b1s+b2sT-b5, BT=b3sexp⁡exp-b4sT-b5,

VfT, P=b7exp⁡[(bsT-bs-b9P)]

T_t  (P)=b₅+b₆P

Generalized reduced gradient (GRG) nonlinear method was used to fit the PVT data into the model. R², coefficient of determination, was also determined for each of the materials. Coefficient of determination is a value between 0 and 1; the more precise data fitting leads to the more accurate model coefficients^[1]. Tait PVT model data and its coefficients are shown in Fig. 1 and Table 1.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Drawn Tait PVT model of (a) PLA, (b) PLA-TPU, (c) and PLA-TPS.

Table 1.

Table 1.

Table 1. Coefficients of curve-fitted (a) the two domain Tait PVT model and (b) cross-WLF model of PLA, PLA-TPU and PLA-TPS Coefficient Unit PLA PLA-TPU PLA-TPS (a) Two domain Tait PVT model b5 K 361.26 462 367.15 b6 K/Pa 7.5E-08 8E-08 1.05E-07 b1m m3/kg 0.000827 0.0008413 0.000844 b2m m3/kg K 8.50E-07 6.38E-07 7.25E-07 b3m Pa 1.63E+08 1.85E+08 1.85E+08 b4m 1/K 0.006196 0.003812 0.005837 b1s m3/kg 0.000821 0.00087 0.000838 b2s m3/kg K 4.47E-07 5.14E-07 3.29E-07 b3s Pa 2.14E+08 2.00E+08 2.45E+08 b4s 1/K 0.006078 0.003398 0.005153 b7 m3/kg 0 0 0 b8 1/K 0 0 0 b9 1/Pa 0 0 0 (b) Cross-WLF viscosity model A1 - 36.10003 1398.752 36.65705 A2 K 1.094729 15375.78 11.57926 D1 Pa s 7.63E+16 4.05E+15 9.20E+16 D2 K 432.0627 145.6926 395.1525 D3 K/Pa 0 0 0 N - 0.01 0.301358 0.607351 Γ Pa 20402.61 27135.87 160.5206

Table 1. Coefficients of curve-fitted (a) the two domain Tait PVT model and (b) cross-WLF model of PLA, PLA-TPU and PLA-TPS

Viscosity‒shear rate relationship of a molten material can be used to predict the rheological behavior once being subjected to shear forces. In this section, the rheology characteristics of the molten thermoplastic materials were determined and the data were further embedded into the Cross-WLF model assisted by data fitting using GRG nonlinear regression method. Seven data fitted coefficients of PLA, PLA-TPU and PLA-TPS blends in Eqs. (4) and (5) are also reported in Table 1. Finally, the obtained coefficients of the model were transferred into Autodesk Moldflow^® database for the injection molding simulations. The Cross-WLF model of the rheological data for the mentioned materials are depicted in Fig. 2.

η=η01+(η0×γ̇Γ)(1-η)(4)

η0=D1exp⁡exp-A1(T-T* )A2+(T-T* ), T* =D2+D×P(5)

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Depiction of fitted Cross-WLF models on (a) PLA, (b) PLA-TPU, (c) and PLA-TPS rheological data.

In the above equations, η (Pa s), γ̇(1/s), T (K), P (Pa) are viscosity, shear rate, temperature and pressure, respectively ^[1]. Table 2 shows the coefficients of determination (R²) for three polymers, which represent the preciseness of implemented model in the data fitting. The R² is calculated using Eq. (6)^[1]. SSE and SST parameters were also calculated using Eqs. (7) and (8).

R2=1-SSESST(6)

SSE=∑(Experimetal data-Model fitted data)2(7)

SST=∑(Experimetal data-Average of experimental data)2(8)

Table 2.

Table 2.

Table 2. Coefficient of determination (R2) PLA PLA-TPU PLA-TPS PVT model 0.974 0.974 0.983 Rheology model 0.979 0.975 0.980

Table 2. Coefficient of determination (R2)

The specific heat capacity of materials was evaluated in the previous works for a wide range of temperatures. Heat capacity evaluation is necessary during solidification of molten material, cooling and heat transfer along the plastic part. Furthermore, steady and balanced heat removal is of great importance for reduction of warpage, shrinkage and internal stress. Moreover, thermal conductivity of each plastic was assumed to be constant at 0.2 W/(m K)^[1].

In the mechanical properties, isotropic features consisting of elastic modulus, shear modulus and alpha (coefficient of thermal expansion) were obtained at around room temperature and embedded in the software for each material.

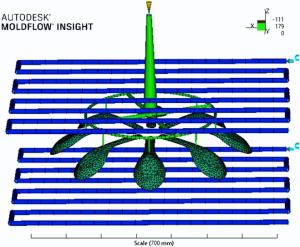
The part model (Fig. 3) was imported into the Autodesk Moldflow^® for the simulation of injection molding process. “ Dual Domain” mesh was used in this analysis that converted the model with triangular elements. The meshed part included 1962 surface triangles, and the average mesh aspect ratio was 2.3739. After the meshing step, the model transferred into a complete multi-cavity design, which included sprue, runner, gate and cooling system, as shown in Fig. 4. The injection location was selected. The best location was recommended by “ Gate Location” analysis.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Designed layout of spoon part.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Spoon cavity design with sprue, runner and cooling channel.

As previously described earlier, the process factors, such as coolant temperature, packing time, packing pressure, mold temperature and melt temperature, were the most significant parameters, which affect warpage and shrinkage of injection-molded part, according to the literature. The simulation was performed by selecting the “ Cool + Fill + Pack + Warp” analysis of these materials to obtain warpage and maximum volumetric shrinkage at the plastic part (spoon). Allrounder 420c 110 ton 7.1 oz (45 mm) (manufactured by Argburg) was determined as the injection molding machine in process simulation. Tool Steel P-20 (manufactured by Generic) was selected as the mold material.

The Taguchi array design was applied to investigate the effect of several process parameters on shrinkage and warpage of the plastic part. The process factors and levels are represented in Table 3. Three reasonable levels were chosen for each factor. For example, melt temperature was set to 185 ° C for level 1 and 205 ° C for level 3 to assure that the melt temperature is well above the material melting points, and degradation does not occur. Meanwhile, the level values were selected in a manner where short shot (incomplete fill) does not happen in the injection process. Very low injection pressure, melt temperature and molding temperatures are the common reasons for the short shot^{[34, 35, 36]}. Other injection parameters, such as filling time and ejection temperature are constant and their values are 1.5 s and 52 ° C, respectively. Injection pressure was switched over after 99% volume filled at the end of the filling stage. Cooling time was automatically determined according to target ejection criteria (i.e. mold temperature and ejection temperature). L₂₇Taguchi array arranged the factors and levels to design the fractional experiments as demonstrated in Table 4.

Table 3.

Table 3.

Table 3. Process factors and their levels Level A: Coolant temperature B: Packing time C: Packing pressure D: Mold temperature E: Melt temperature (° C) (s) (% Injection pressure) (° C) (° C) 1 8 8 75 25 185 2 13 20 85 30 195 3 18 32 95 40 205

Table 3. Process factors and their levels

Table 4.

Table 4.

Table 4. 27 (35) Taguchi orthogonal array Trial No. Control factors Trial no. Control factors A B C D E A B C D E 1 1 1 1 1 1 15 2 2 3 1 3 2 1 1 1 1 2 16 2 3 1 2 1 3 1 1 1 1 3 17 2 3 1 2 2 4 1 2 2 2 1 18 2 3 1 2 3 5 1 2 2 2 2 19 3 1 3 2 1 6 1 2 2 2 3 20 3 1 3 2 2 7 1 3 3 3 1 21 3 1 3 2 3 8 1 3 3 3 2 22 3 2 1 3 1 9 1 3 3 3 3 23 3 2 1 3 2 10 2 1 2 3 1 24 3 2 1 3 3 11 2 1 2 3 2 25 3 3 2 1 1 12 2 1 2 3 3 26 3 3 2 1 2 13 2 2 3 1 1 27 3 3 2 1 3 14 2 2 3 1 2 - - - - - -

Table 4. 27 (35) Taguchi orthogonal array

ANNs are capable of dealing with linear and nonlinear functions, and their major application is in the area of forecasting^[37]. In this study, a feed-forward back-propagation-based ANN solver, provided by IBM SPSS Modeler 14.2 was used. Multilayer perceptron includes a large group of feed-forward neural networks with different number of layers. The multilayer perceptron ANNs were created with the common learning algorithm of feed-forward back-propagation (FFBP) for each 27 experiments group (Taguchi orthogonal arrays) as the training sample. The parameters of the model, such as selection of input nodes, number of hidden layers and hidden nodes, and the form of transfer functions are dependent on the problem and often are specified using trial and error. Ghiasi and Nangoy studies show that the ideal number of hidden layers in FFBP algorithm is often 1 or 2, although there are fewer guidelines on the optimal number of hidden nodes^[38]. To find the optimal network that allows most accurate ANNs for fitting target, different numbers of hidden layers (1 and 2) and nodes (9-15) in every hidden layer were tested, and then, the bests were selected. The inputs were control factors from A to E in the levels of 1, 2 or 3 and the target was the shrinkage percentage, warpage or average of normalized shrinkage and warpage.

To establish the more accurate ANN for each material and each target (warpage, shrinkage or average of normalized shrinkage and warpage), the 56 architectures (with 1 or 2 hidden layers each containing 9 to 15 nodes) were established. Training accuracy (R²) of ANNs was obtained according to the comparison of outputs of ANN and Autodesk Moldflow for each of the 27 experiments. The stopping rules include a limit of desired accuracy, number of maximum training cycles that the model would run, and the maximum training time which the model is allowed to run. In this project, both stopping rules of maximum training time of 15 min and minimum accuracy of 99.9 were selected to ensure that the resulting model meets high accuracy. Overall, between each 56 architectures for each material and target, only 1 with higher training R² is selected. Afterwards, for the highest training accuracy models, forecasting sets (out of 27 training sets) were also tested. The generally accepted guideline of 80% for training (27 training set) and 20% for forecasting (7 forecasting set) of experiments were used^[38]. The training R² based on mean squared error was calculated by the software but the forecasting R² was calculated using Eq. (6). Table 5 shows the performance of the optimum ANNs.

Table 5.

Table 5.

Table 5. Characteristics and performances of the six optimum ANNs Samples Warpage Shrinkage Average of normalized shrinkage and warpage R12 R22 N1 N2 R12 R22 N1 N2 R12 R22 N1 N2 PLA 0.9991 0.9673 9 9 0.9993 0.9834 10 12 0.9990 0.9851 8 12 PLA-TPU 0.9990 0.9782 15 15 0.9995 0.9648 9 9 0.9992 0.9765 15 15 PLA-TPS 0.9991 0.9741 15 15 0.9995 0.9782 15 15 0.9991 0.9573 14 15 N1 = Number of neurons in the first hidden layer. N2 = Number of neurons in the second hidden layer. R12 = Training R2. R22 = Forecasting R2.

Table 5. Characteristics and performances of the six optimum ANNs

Shrinkage and warpage behaviors may be affected by many parameters, such as material combination and processing factors. It is commonly accepted that semi-crystalline polymers have less resistance to warpage and shrinkage compared to amorphous ones because of the closer packing of the crystalline structure^{[13, 17]}. Higher volumetric shrinkage indicates that the material of the plastic part has a greater transition of specific volume. In other words, extensive crystallization happens in the course of solidification of molten material during cooling process^[1]. It means that the volumetric shrinkage is influenced from the compressibility properties of the polymer material through the PVT properties. However, warpage depends on the phenomenon of the polymer shrinkage. Actually, warpage happens when non-uniform shrinkage occurs in the plastic part. Generally, a low degree of crystallinity results in the reduction of shrinkage and thereby reducing warpage in semi-crystalline polymers^[39]. In this study, PLA and PLA-TPU have the highest and the lowest degree of crystallinity among the used polymers, respectively. PLA crystallization for PLLA is normally between 37% and 42%^{[40, 41]}, however, in this work, crystallization is 42% reported in Ref.^[31]. By melt mixing of TPU and PLA due to the existence of another polymer and its low crystallization rate^[42], the crystallinity is highly declined^[43]. The same phenomenon happens for the PLA-TPS and the crystallinity is decreased; however, this increase is lower than PLA-TPU blends since the starch can act as a nucleating agent in the PLA matrix^[29]. Fig. 5 indicates the volumetric shrinkage behaviors of PLA, PLA-TPU and PLA-TPS in the same process conditions (typically trial 8 from Table 4). Regions in red have the highest volumetric shrinkage defects. As can be seen in Fig. 5, the maximum volumetric shrinkage in plastic spoon part for PLA, PLA-TPU and PLA-TPS are 9.724%, 5.071% and 5.305%, respectively. Fig. 6 shows the deflection (warpage) effect in three components (x, y, and z) for PLA, PLA-TPU and PLA-TPS in the same process conditions (trial 8). Sections in red have the most deflection defects in the part. Here, the most deflection also occurs in the PLA part (1.428 mm). On the contrary, the PLA-TPU part has the lowest warpage (0.5302 mm).

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Shrinkage of (a) PLA, (b) PLA-TPU, and (c) PLA-TPS.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Warpage of (a) PLA, (b) PLA-TPU, and (c) PLA-TPS.

According to the results, the PLA spoon has exhibited the worst resistance to warpage and shrinkage defects compared to the other two spoons. This behavior can be further explicated by the highest crystallinity of the PLA, which results in the highest level of shrinkage and thereby warpage in PLA spoon. Due to the lower price of starch compared to the other polymers in this system and use of 50:50 wt% blend PLA-TPS, it can be the best alternative to produce spoon. PLA-TPU is also cost-effective but not cheaper than PLA-TPS. However, based on the Autodesk Moldflow^® results, PLA-TPU has the best results.

In order to measure the output quality and characteristics (warpage and shrinkage), Taguchi has utilized the signal-to-noise (S/N) ratio according to Eqs. (9) and (10). S/N ratio measures the sensitivity of a parameter to uncontrollable factors. The terms “ signal” and “ noise” stand for desirable and undesirable quality values, respectively. The goal of Taguchi is not only optimization of control factors, but also reduction of sensitivity of engineering designs to uncontrollable factors (noises). Taguchi proposed to maximize S/N ratio due to reduction of product variance around the target value^[13]. The quality characteristic in the S/N ratio analysis is smaller-the-better, because the target is to minimize warpage as well as volumetric shrinkage at the part, where MSD is the mean square deviation, y is the experiment value and n represents the number of tests in one trial ^[18].

S/N=-10log(MSD) (9)

MSD=1n∑i=1nyi2(10)

Fig. 7 and Fig. 8 represent the S/N ratios of warpage and shrinkage for different polymers, respectively. The higher the S/N ratio for each factor gave the better process conditions. As can be observed in Fig. 7, the effects of changing levels on the warpage are different for each polymer. For example, S/N ratio is increased by increasing the E factor (melt temperature) for the PLA and PLA-TPS parts. This observation indicates that the warpage is reduced. On the contrary, S/N ratio is decreased by increasing the E factor for the PLA-TPU. However, with increasing the C factor (packing pressure) S/N ratio is generally increased for all of the applied polymers, and therefore, the warpage is decreased.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. S/N ratio of control factors for warpage response.

According to Fig. 8, the effects of changing levels of factors on the shrinkage are also different for three polymers. However, C factor has the same effect on shrinkage for three polymers, like warpage. These results are in agreement with the observations in previous reports^{[11, 25, 44, 45]}, which indicates that higher packing pressure causes lower shrinkage and warpage on the plastic part.

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. S/N ratio of control factors for shrinkage response.

The ANOVA is used in order to investigate the most significant factors affecting the quality of the final product^[13]. The ANOVA results for warpage and shrinkage are given in Table 6. The results show the best combination of factors and levels to maximize S/N ratio, which causes less sensitivity of uncontrollable factors during production. Here, the percentage contribution (C%) of variances or factors is calculated after determining quantities of degree of freedom (f), sum of squares (SS), and variance (V) according to Eqs. [11, 12, 13, 14, 15, 16, 17]. The determination of these values was illustrated for Factor A and interaction AB as a sample; calculation of all factors and their binary interactions are reported in Table 6.

Total degree of freedom,  f_T​: f_T=N-1=27-1=26 (11)

where N is the total number of results.

Degree of freedom for Factor A,  f_A​: f_A=k_A-1=3-1=2 (12)

Table 6.

Table 6.

Table 6. ANOVA table for (a) warpage, (b) shrinkage, and (c) average of normalized shrinkage and warpage (a) ANOVA warpage Source PLA PLA-TPU PLA-TPS f SS V C% Best level SS V C% Best level SS V C% Best level A 2 0.0004 0.0002 0.265 1 0.0398 0.0199 2.163 1 0.0433 0.0216 2.059 3 B 2 0.0002 0.0001 0.131 3 0.1032 0.0516 5.615 1 0.0234 0.0117 1.114 1 C 2 0.0107 0.0054 7.094 3 0.1138 0.0569 6.189 3 0.0645 0.0323 3.067 3 D 2 0.0001 0.0001 0.075 3 0.1859 0.093 10.113 3 0.3814 0.1907 18.132 3 E 2 0.1033 0.0517 68.441 3 0.0611 0.0305 3.321 1 0.0031 0.0016 0.148 3 AB 4 0.0108 0.0027 7.169 1 3 0.2997 0.0749 16.302 1 3 0.4459 0.1115 21.197 1 3 AC 4 0.0003 0.0001 0.206 1 3 0.2891 0.0723 15.727 1 3 0.4048 0.1012 19.244 1 3 AD 4 0.0109 0.0027 7.225 1 3 0.217 0.0542 11.804 1 3 0.0879 0.022 4.181 1 3 AE 4 0.0008 0.0002 0.554 3 3 0.0011 0.0003 0.058 1 1 0.0094 0.0024 0.447 3 1 BC 4 0.0005 0.0001 0.34 3 3 0.2257 0.0564 12.275 3 3 0.4247 0.1062 20.189 3 3 BD 4 0.0111 0.0028 7.359 3 3 0.1535 0.0384 8.352 3 3 0.1078 0.027 5.126 3 3 BE 4 0.0002 0.0001 0.155 1 3 0.002 0.0005 0.108 1 1 0.0034 0.0009 0.162 1 3 CD 4 0.0006 0.0001 0.396 3 3 0.143 0.0357 7.777 3 3 0.0667 0.0167 3.172 3 3 CE 4 0.0005 0.0001 0.354 3 3 0.0009 0.0002 0.051 3 1 0.0054 0.0014 0.259 3 2 DE 4 0.0003 0.0001 0.23 3 3 0.0027 0.0007 0.144 3 1 0.0317 0.0079 1.507 3 3 Total 26 0.1509 — 100 — 1.8383 — 100 — 2.1038 — 100 — (b) ANOVA shrinkage Source PLA PLA-TPU PLA-TPS f SS V C% Best level SS V C% Best level SS V C% Best level A 2 0.0445 0.0222 0.752 1 0.0343 0.0172 0.285 1 0.0016 0.0008 0.012 3 B 2 0.2489 0.1244 4.207 1 0.4682 0.2341 3.889 3 0.00001 0 0.0001 2 C 2 0.5518 0.2759 9.327 3 1.7728 0.8863 14.725 3 1.3846 0.6923 10.711 3 D 2 0.4055 0.2028 6.855 1 0.0408 0.0204 0.339 3 0.7276 0.3638 5.628 1 E 2 0.3834 0.1917 6.48 3 2.772 1.386 23.025 1 4.4335 2.2168 34.298 1 AB 4 0.9573 0.2393 16.183 2 2 1.8136 0.4534 15.064 1 3 2.1122 0.528 16.34 2 2 AC 4 0.6544 0.1636 11.063 2 3 0.509 0.1273 4.228 1 3 0.7276 0.1819 5.628 2 3 AD 4 0.8007 0.2002 13.535 2 1 2.241 0.5603 18.614 1 3 1.3846 0.3462 10.712 2 1 AE 4 0.0756 0.0189 1.277 3 3 0.0007 0.0002 0.005 1 1 0.0002 0.0001 0.002 3 1 BC 4 0.45 0.1125 7.608 2 3 0.0752 0.0188 0.624 3 3 0.7291 0.1823 5.641 2 3 BD 4 0.5963 0.1491 10.08 2 1 1.8071 0.4518 15.01 3 3 1.3862 0.3466 10.724 2 1 BE 4 0.2997 0.0749 5.066 2 3 0.0008 0.0002 0.007 2 1 0.0014 0.0004 0.011 3 1 CD 4 0.2934 0.0733 4.96 3 1 0.50264 0.1256 4.174 3 3 0.0016 0.0004 0.0123 3 1 CE 4 0.078 0.0195 1.319 3 3 0.001 0.0002 0.008 3 1 0.0345 0.0086 0.267 3 1 DE 4 0.0761 0.019 1.287 1 3 0.0004 0.0001 0.003 3 1 0.0018 0.0005 0.014 1 1 Total 26 5.9155 — 100 — 12.0393 — 100 — 12.9266 — 100 — (c) ANOVA average of normalized shrinkage and warpage Source PLA PLA-TPU PLA-TPS f SS V C% Best Level SS V C% Best level SS V C% Best level A 2 0.0002 0.0001 0.058 1 0.016 0.008 1.69205 1 0.0094 0.0047 1.657 3 B 2 0.0007 0.00035 0.203 1 0.0044 0.0022 0.46531 1 0.0047 0.00235 0.82849 1 C 2 0.0061 0.00305 1.766 3 0.1238 0.0619 13.09222 3 0.0462 0.0231 8.14384 3 D 2 0.0013 0.00065 0.376 1 0.0596 0.0298 6.30288 3 0.0688 0.0344 12.12762 1 E 2 0.0178 0.0089 5.152 3 0.1284 0.0642 13.57868 1 0.0408 0.0204 7.19196 1 AB 4 0.0073 0.00183 2.113 3 1 0.1834 0.0459 19.39509 1 3 0.115 0.02875 20.27146 2 2 AC 4 0.002 0.0005 0.579 3 3 0.064 0.016 6.76819 1 3 0.0734 0.01835 12.93848 2 3 AD 4 0.0068 0.0017 1.968 3 2 0.1282 0.0321 13.55753 1 3 0.0509 0.01273 8.97233 2 1 AE 4 0.0004 0.0001 0.116 3 3 0.0004 0.0001 0.0423 1 1 0.002 0.0005 0.35255 2 1 BC 4 0.0015 0.00038 0.434 1 3 0.0756 0.0189 7.99492 3 3 0.0781 0.01953 13.76697 2 3 BD 4 0.0063 0.00158 1.823 1 2 0.1398 0.035 14.78426 3 3 0.0556 0.0139 9.80081 2 1 BE 4 0.001 0.00025 0.289 1 3 0.0007 0.00018 0.07403 3 1 0.0006 0.00015 0.10576 2 1 CD 4 0.2934 0.07335 84.92 3 2 0.0203 0.00508 2.14679 3 3 0.014 0.0035 2.46783 3 1 CE 4 0.0005 0.00013 0.145 3 3 0.0004 0.0001 0.0423 3 1 0.0013 0.00033 0.22916 3 1 DE 4 0.0002 0.00005 0.058 2 3 0.0006 0.00015 0.06345 3 1 0.0065 0.00163 1.14578 1 1 Total 26 0.3455 — 100 — 0.9456 — 100 — 0.5673 — 100 —

Table 6. ANOVA table for (a) warpage, (b) shrinkage, and (c) average of normalized shrinkage and warpage

Sum of square, SS:

SSA=(∑(A1)2kA+(∑(A2)2kA+(∑(A3)2kA-(y1+y2+⋯+yN)2N(13)

SSAB=(∑(A1B1)2kAkB+⋯+∑(A3B32kAkB-(y1+y2+⋯+yN)2N(14)

SST=∑(SSA+⋯+SSE+SSAB+⋯+SSDE)(15)

where ∑ A_i stands for sum of the y_j when Factor A is in the ith level.

Variance for Factor A, V_A: VA=SSAfA(16)

Percentage contribution, C% for Factor A: C%= SSASST×100(17)

Percentage contribution (C%) shows which factors have a greater impact on warpage and shrinkage of the plastic spoon. The higher C% indicates the more importance of a factor.

As can be seen in Table 6(a) (warpage), melt temperature (E) with 68.441% of the contribution for PLA, the combination of coolant temperature and packing time (A ×  B) with 16.302% of the contribution for PLA-TPU and 21.197% of the contribution for PLA-TPS give the highest influence on warpage. On the other hand, from Table 6(b) (shrinkage) the combination of coolant temperature and packing time (A ×  B) with 16.183% of the contribution for PLA, melt temperature (E) with 23.025% of the contribution for PLA-TPU and 34.289% of the contribution for PLA-TPS are the most effective factors on shrinkage. The best level for each factor is the one that achieves maximum S/N ratio value compared to the other levels as shown in Table 6. The best level selection for binary interactions is the binary level when S/N ratio is maximum. Each factor or binary interaction has three and nine (3× 3) level states, respectively. The final optimal level selection is not as simple as selection of the best level for all factors and interactions because of the contribution of single factors and binary interactions. In order to solve this year, factors and interactions were aliened based on their percentage contribution; the highest percentage contribution of each factor in single factor and interaction has the strongest criterion in selection of optimal level of the factor^[13]. Table 7 represents the optimal level selection for each factor in the warpage and shrinkage analysis of the three materials. Due to the use of automatic injection pressure, the packing pressure (C) level selection do not define a particular pressure values as materials or conditions change, and therefore their specific values are shown along their level selection in the Table 7. The optimal level selection of control factors to reach the lower warpage and shrinkage based on ANOVA lead to 1.359, 0.4647 and 0.5984 mm warpage and 6.923, 1.791 and 2.728% shrinkage for PLA, PLA-TPU and PLA-TPS, respectively. In addition, after the minimization of shrinkage and warpage simultaneously, i.e. after averaging the normalized shrinkage and warpage by using ANOVA (based on Table 7), shrinkage and warpage of PLA, PLA-TPU and PLA-TPS become “ 7.025%, 1.367 mm” , “ 1.791%, 0.4647 mm” and “ 2.728%, 0.6928 mm” , respectively. The results of simultaneously lowering shrinkage and warpage are highly desirable and their pertaining conditions are efficacious in practice.

Table 7.

Table 7.

Table 7. The level selection of factors for warpage, shrinkage and average of normalized shrinkage and warpage optimization based on ANOVA and ANN results PLA PLA-TPU PLA-TPS A B C D E A B C D E A B C D E Warpage ANOVA C% 7.2 7.4 7.1 7.4 68.4 16.3 16.3 15.7 11.8 3.3 21.2 21.2 20.2 19.2 1.5 Optimal Level 1 3 3(7.05 MPa) 3 3 1 3 3(58.71 MPa) 3 1 1 3 3(30.75 MPa) 3 3 ANN Optimal Level 2 3 3(6.96 MPa) 3 3 1 3 3(58.71 MPa) 3 1 2 3 3(32.72 MPa) 3 3 Shrinkage ANOVA C% 16.2 16.2 11.1 13.5 6.5 18.6 15.1 14.7 18.6 23.0 16.3 16.3 10.7 10.7 34.3 Optimal Level 2 2 3(7.76 MPa) 1 3 1 3 3(58.71 MPa) 3 1 2 2 3(55.04 MPa) 1 1 ANN Optimal Level 1 1 3(7.07 MPa) 1 3 1 3 3(58.71 MPa) 3 1 3 2 3(56.06 MPa) 1 1 Average of normalized shrinkage and warpage ANOVA C% 2.1 2.1 84.9 84.9 5.2 19.4 19.4 13.1 14.8 13.6 20.3 20.3 13.8 12.1 7.2 Optimal Level 3 1 3(7.80 MPa) 2 3 1 3 3(58.71 MPa) 3 1 2 2 3(55.04 MPa) 1 1 ANN Optimal Level 3 1 3(7.07 MPa) 1 3 1 3 3(58.71 MPa) 3 1 3 2 3(55.14 MPa) 2 1

Table 7. The level selection of factors for warpage, shrinkage and average of normalized shrinkage and warpage optimization based on ANOVA and ANN results

As represented in Table 5, the training and forecasting R² for each created ANN is higher than 0.95, which shows high accuracy of the fitted models on each 27 experiments group and their predictions. The optimal level selection of control factors based on ANN with warpage targets result in outputs of 1.360, 0.4647 and 0.6285 mm for PLA, PLA-TPU and PLA-TPS, respectively. Moreover, the optimal level selection extracted from ANN models with shrinkage targets results in 6.917, 1.791 and 2.670% shrinkage for PLA, PLA-TPU and PLA-TPS, respectively. Furthermore, for the minimization of shrinkage and warpage at the same time, i.e. after averaging normalized shrinkage and warpage, using the optimal level selection of factors predicted by ANN as reported in Table 7, the shrinkage and warpage of PLA, PLA-TPU and PLA-TPS become 7.0312% (1.361 mm), 1.791% (0.4647 mm) and 2.8127% (0.6273 mm), respectively. The ANN optimal level selection and pertaining targets (warpage, shrinkage or average of normalized shrinkage and warpage) are almost in agreement with ANOVA optimal level selection and obtained targets. Although ANN and ANOVA optimal targets are different in some cases, they are so close that their differences are considered negligible. Surprisingly, the ABCDE optimal level selections of warpage, shrinkage, and average of normalized shrinkage and warpage for PLA-TPU are the same, i.e. 13331, and more notably, its shrinkage and warpage are significantly lower than those of PLA and PLA-TPS. Thus, the very low warpage and shrinkage of PLA-TPU is added to its good processability, biocompatibility, biodegradability, and relative cost-effectiveness, which makes it a good injectable plastic and is applicable even in the food contactable usage.