Cite this Article
Jian-Feng Wen, Shan-Tung Tu, Fu-Zhen Xuan, Xue-Wei Zhang, Xin-Lin Gao. Effects of Stress Level and Stress State on Creep Ductility: Evaluation of Different Models. Journal of Materials Science & Technology, 2016, 32: 695-704  
Permissions
Copyright reserved, Editorial board of Journal of Materials Science & Technology
Received:2016-02-03
Effects of Stress Level and Stress State on Creep Ductility: Evaluation of Different Models
Jian-Feng Wen1,2, Shan-Tung Tu1,*, Fu-Zhen Xuan1, Xue-Wei Zhang1, Xin-Lin Gao3
1 Key Laboratory of Pressure Systems and Safety (Ministry of Education), School of Mechanical and Power Engineering, East China University of Science and Technology, Shanghai 200237, China
2 Department of Materials Science and Engineering, Texas A&M University, College Station, TX 77843, USA
3 Department of Mechanical Engineering, Southern Methodist University, Dallas, TX 75275-0337, USA
Corresponding author. Ph.D.; Tel.: +86 21 64253425; Fax: +86 21 64253513.E-mail address: sttu@ecust.edu.cn (S.-T. Tu).
Abstract

The last few decades have witnessed an increasing emphasis on the development of strain-based approach for predicting the creep life or damage of components operating at elevated temperatures. Creep ductility, as a key parameter in this approach, may vary with a number of factors including strain rate, state of stress, operating temperature, material microstructure, etc. The present paper, however, is focused on reviewing the state-of-the-art understanding of the effects of stress level and stress state on the creep ductility. Mechanisms involving the void growth and coalescence are presented to describe the role of stress level in the variation of uniaxial creep ductility. The prediction capacity of existing empirical ductility models is also assessed in light of uniaxial test data. On the other hand, a vast body of multiaxial creep test data, collected from open literature, is utilized to examine the influence of the state of stress on the creep ductility. Then, a variety of multiaxial ductility factor models are introduced and evaluated with the available experimental data. Finally, a brief discussion on the dependence of creep ductility on the stress triaxiality and Lode parameter, predicted by numerical methods, is provided.

Keyword: Creep; Creep ductility; Multiaxial stress state; Ductility exhaustion

Nomenclature

β i(i  = 0, 1, 2, 3…) material constants in empirical ductility models

σ applied stress

ω ccreep damage variable

ε ccreep strain

creep strain rate

Δ ltrielongation of the matrix under triaxial stress state

Δ lunielongation of the matrix under uniaxial stress state

σ eqequivalent (von Mises) stress

ω ffatigue damage variable

σ mhydrostatic stress

inelastic strain rate

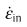
ε Llower shelf for uniaxial creep ductility

α material constant of multiaxiality in stress-based models

σ 1maximum principal stress

multiaxial creep ductility

σ rrupture stress (representative stress)

σ 2secondary principal stress

σ btensile strength

σ 3third principal stress

ε funiaxial creep ductility

ε Uupper shelf for uniaxial creep ductility

σ 0.2yield strength

l half distance between voids

L Lode parameter

MDF multiaxial ductility factor

n steady-state creep exponent

p material constants in Spindler model

P2/P1biaxial stress ratio

q material constants in Spindler model

rhradius of growing void

T temperature

t time

trtime to rupture

1. Introduction

The history of industrial civilization in human society has witnessed the continued rise of operating temperatures for machines since the industrial revolution. The use of higher temperatures not only improves the efficiency in energy conversion systems, but also imposes more requirements for the safety of materials and structures. One of the dominant failure mechanisms for components operated at elevated temperatures is creep fracture[1]. The challenge to both academia and industry, therefore, is to develop techniques that will permit more reliable and effective assessment of the integrity of critical components under creep conditions.

Basically, models to evaluate the creep life or damage fall into two main categories. The first one is based on Robinson's life fraction rule[2], in which the indicator of creep damage, ω c, can be expressed in the form

ωc=∫dttτ(σ, T)(1)

where t is the time spent at a given applied stress, σ , and a given temperature, T. Since the time to rupture, tr, is a function of the applied stress, this time fraction concept actually coincides with the stress-based approach. This concept results in a simple mathematical analysis and has been commonly used in high temperature design codes such as ASME BPVC Section III-NH[3], RCC-MRx[4] and life assessment guidelines such as BS7910[5]. However, uniaxial creep rupture experiments have already demonstrated that the life fraction rule cannot be valid for stress-change conditions[6]. In addition, although long-term test results are still limited in the literature, some uniaxial creep-fatigue data have shown that the time fraction approach may be overly conservative for high stress dwells and non-conservative for relatively low stress dwells[7], as shown in Fig. 1.

Fig. 1. Comparison of creep damages calculated by life fraction rule and ductility exhaustion concept in calculating damages for 316H stainless steel at 570 ° C (linear interaction, /3 and × 3 denote ω c+ω f=1, 1/3 and 3, respectively): (a) creep-fatigue interaction diagram; (b) total damage vs stress dwell (adapted from Reference [7]).

Under multiaxial stress conditions, the life fraction rule (stress-based approach) may extremely underestimate the creep life in many relaxation-predominant cases. For example, Isobe et al.[8] revealed that the stress-based approach could overestimate the creep damage by a factor of 500 in a notched bar of a low alloy steel. This is mainly because the representative stresses are high at early stage of life, and unrealistically large amounts of damage are calculated using these stresses. It is also worth mentioning that the widely-accepted Kachanov-like damage evolution laws[9] can also be phrased as Eq. (1), in which Hayhurst[10] suggested that the rupture stress should be employed instead of σ to incorporate the effect of multiaxial stress states. The rupture stress (representative stress) is defined by

σ r=α σ 1+(1-α )σ eq(2)

where σ 1 and σ eq are the maximum principal and von Mises stress, respectively. The material constant α reflects the effect of multiaxial stress states and is in the range of 0 to 1. However, different values of α are obtained by different investigators [11, 12, 13, 14], as listed in Table 1. It must be pointed out that predictions are extremely sensitive to this material constant, e.g., a tiny decrease of α from 0.57 to 0.52 may cause a dramatic increase of 47.34% of the predicted failure time for compact tension (CT) specimens of P91 steel [15]. These uncertainties of the representative stresses and the material constants are insurmountable obstacles to accurate assessment by using the stress-based approach.

Table 1. Material constant α for 316 stainless steel

The alternative scheme now gaining favor is the strain-based approach for evaluating the creep life or damage, which can be given as follows:

ωc=∫dεcεf* (3)

where ε c and εf* are creep strain and multiaxial creep ductility, respectively. This approach is based on the ductility exhaustion concept, in which the failure is assumed to occur when the locally accumulated creep strain reaches a critical value. Since the components operating at high temperatures are often subjected to a multiaxial state of stress imposed by an alteration of geometry, material or loading in service, εf* normally differs from the uniaxial creep ductility, ε f, which is usually determined by the strain to failure in a constant load creep test. It should be noted that the creep ductility can be defined in terms of either elongation or reduction in area. For the purpose of concision and consistency, the same symbol, ε f, will be used in the present paper. The ductility exhaustion concept for calculating creep damage has already been included into the R5 guidelines[16, 17] and widely incorporated with finite element techniques for predicting the initiation and growth of creep cracks in carbon-manganese steel[18, 19, 20], austenitic stainless steels[21, 22, 23, 24], ferritic heat resistant steels[25, 26], coppers[27, 28], structural ceramics[29], etc. Extensive studies[30, 31, 32, 33, 34]have proven that the strain-based approach (ductility exhaustion concept), if the creep ductility is appropriately given, may offer more accurate predictions of life under cyclic loading than the stress-based approach (life fraction rule), as shown in Fig. 1 for 316H stainless steel at 570 ° C[7].

Undoubtedly, creep ductility (creep failure strain) is a key parameter when creep damage or creep crack growth rate[35] is estimated by using the strain-based approach. Nevertheless, a criticism that may usually be leveled is the difficulty to deal with the complex change in the creep ductility: one is concerned with the variation of uniaxial creep ductility over wide ranges of strain rate (stress level); another refinement that needs to be heeded is the effect of multiaxial states of stress on creep failure strain. In the present work, therefore, we intend to concentrate primarily on these two aspects of great importance and to provide a better understanding of them.

2. Stress Dependence of Uniaxial Creep Ductility
2.1. Mechanisms of stress-level effect

It is widely accepted that the mechanisms of creep fracture are involved with wedge-type cracking at grain boundary triple points or with nucleation of cavities followed by growth and coalescence at grain boundaries. Since initiation[36] and propagation[37] of some wedge-type cracks may also be caused by cavity formation, we will only focus on studies on creep cavitation hereinafter. Fig. 2(a) and (b) presents a typical steady-state growth of creep cavities in Inconel 718[38] and combination of developed cavities in Waspaloyalloy[39], respectively. With respect to cavity nucleation, three mechanisms including vacancy accumulation[40], grain boundary sliding[41] and dislocation pile-ups[42] are supposed to be the likely driving forces. Nevertheless, it is still unclear which mechanism is dominant at the nucleation stage[43]. Thus, only subsequent growth and coalescence of cavities will be mainly discussed in the present paper.

Fig. 2. Micrograph of creep cavities at grain boundaries: (a) steady-state growth of cavities in Inconel 718 alloy at 650 ° C[38]; (b) interlinkage of cavities in Waspaloy alloy at 700 ° C[39].

By virtue of the relative simplicity of testing and convenience of strain measurement, overwhelming majority of creep ductility data are obtained from uniaxial creep tests, e.g., Reference [44]. However, uniaxial strain to failure may vary with stress level/rupture time/strain rate in an intricate style. Generally, rupture ductility is expected to be high at high stress levels and low at low stress levels. For instance, Holdsworth[45] proposed that the rupture elongation vs rupture time curve for ferritic steels can be roughly divided into four regimes, as illustrated in Fig. 3. In Regime-I, ductile rupture occurs mainly due to the formation of voids arising from particle/matrix decohesion. Followed is Regime-II, characterized by a remarkable drop in rupture ductility, which is caused by the increasing grain boundary cavities and by relatively evident matrix deformation. The lower plateau, Regime-III, involves the formation and diffusion-controlled cavity growth at grain boundaries. In a longer term, rupture ductility recovers to some extent, resulting from the suppressive cavity nucleation and growth associated with the over-aging of microstructure in Regime-IV. This four-regime description is consistent with the dataset of rupture elongation for a heat resistant steel[46] (X19CrMoVNb11-1) at different temperatures but has not received much attention.

Fig. 3. Effect of rupture time on rupture ductility (adapted from Reference [45]).

Another regime splitting method receiving more acceptance was proposed by Hales[47].Fig. 4(a) shows the schematic representation of the strain rate effect on rupture ductility. In Regime-I with high strain rates, the failure is mainly controlled by cavity growth due to the viscoplastic deformation of the surrounding matrix[48, 49, 50, 51], as depicted inFig. 4(b), resulting in a constant strain to failure. Cavity growth governed by vacancy diffusion[52, 53] on the boundary/surface is illustrated in Fig. 4(c), with the assumption that the grains are rigid. As the stress level reduces, this mechanism is predominant, leading to a decline of the creep ductility in Regime-II. At low stress levels, cavitation is expected to be heterogeneous, and the creep deformation of the uncavitated areas is slow enough to constrain the diffusion growth of inter-granular cavities[54, 55, 56, 57], as represented in Fig. 4(d) for Regime-III. The constrained diffusion cavity growth also predicts a creep ductility independent of the strain rate and offers a lower limit. It needs to be noted that which mechanism of cavity growth is dominant depends on the material properties, prevailing temperature and applied stress. Some useful clues can also be seen in a book of fracture at high temperatures by Riedel[58], review articles by Needleman and Rice[59], Kassner and Hayes[60] and Lin et al.[61], and particularly void growth maps constructed by Cocks and Ashby[62].

Fig. 4. Effect of strain rate on rupture ductility: (a) schematic representation of regimes (adapted from Reference[47]); (b) Regime-I: viscoplastic cavity growth; (c) Regime-II: diffusion controlled cavity growth; (d) Regime-III: constrained diffusion cavity growth.

Three regimes of creep ductility can be identified from a number of datasets of uniaxial creep test (see References [44] and [63]). Variation of creep ductility (in terms of axial displacement) against stress (normalized by the flow stress) for 316H stainless steel at 550-700 ° C subjected to different heat treatments is presented in Fig. 5<sup>[64, 65]. Within the range of data scatter, the experimental uniaxial creep ductility for this austenitic type stainless steel at 600-700 ° C can be divided into three regimes. Although creep ductility data at 550 ° C are available only at a very high stress level and show significant scatter in test data, Mehmanparast et al.[64, 65, 66] assumed a similar three-regime tendency of data at 550 ° C (see Fig. 5), and the predicted creep crack growth (CCG) results based on stress dependent uniaxial properties show a good agreement for both the short and long term CCG data in different specimen geometries. For a Cr-Mo-V steel (25Cr2NiMo1V), in a similar way, different CCG rates observed experimentally for a wide range of C* -integral (stress level) [67, 68] have been reproduced by using the stress-regime dependent creep ductility implemented in a strain-based approach[69]. It is natural to think that the value of higher/lower plateau and the slope of transition region of stress-regime dependent creep ductility may have potential impact on the predicted CCG rates. More detailed sensitivity analyses can be seen in Reference [70].

Fig. 5. Variation of creep ductility (in terms of axial displacement) against normalized stress for 316H at 550-700 ° C (adapted from References [64] and [65]).

Fig. 6(a, b) shows the relations between creep ductility (in terms of reduction in area) and stress (normalized by the 0.2% offset yield stress[72]) for martensitic 9%-12% chromium steels, T92, P92, T122 and P122 at 550-700 ° C[71]. Clearly, higher and lower shelves have been observed in relatively high and low stress levels, respectively. It also has been seen that there is a remarkable decline of creep ductility at normalized stresses near 0.5 with decrease in the stress level, without obvious temperature dependency. Kimura et al.[71]explained that the significant drop in the rupture ductility was mainly contributed by the shift of stress condition from plastic regime in the short term to elastic regime in the long term. They believed that a relatively high ductility in the high-stress regime was provided by an easy plastic deformation, and a creep deformation concentration in a recovered region led to a low ductility. It is also observed that the creep ductility of T91 declines drastically only at 650 ° C and that of Gr. 91 steel does not indicate significant drop, as shown in Fig. 6(c). It must be pointed out that this might not be the case if the creep ductility data at low stress levels are sufficient. However, differences of impurity such as Al, P, S, Sn, As and Sb may also be considered to be responsible for the different behaviors of the ductility[73].

Fig. 6. Variation of creep ductility (in terms of reduction in area) against normalized stress at 500-700 ° C (adapted from Reference [71]): (a) T92 and P92; (b) T122 and P122; (c) T91 and Gr.91.

2.2. Empirical ductility models describing stress-level effect

There have been a number of studies on the empirical models describing the uniaxial creep ductility, which is generally characterized as a function of temperature, stress and/or strain rate. For example, the empirical ductility model in R5-2003 procedures[17] can be given as follows:

εf=min⁡(εij, max⁡(εL, β0exp⁡(β1T)ε̇cβ2))(4)

where β i (i  = 0, 1, 2, etc.) are the material constants. Stress-independent upper shelf, ε U, and lower shelf, ε L, are usually defined by the elongation at failure measured from tensile tests and the creep strain to failure of long term creep data, respectively, at a corresponding temperature, T. The transition region is defined using a regression analysis of creep data exhibiting a decreasing ductility with decreasing creep strain rate, ε̇c. This treatment is a significant aspect of the R5 ductility exhaustion approach and Eq.(4) performs well in general. However, it is pointed out that R5-2003 approach may give overly conservative predictions of creep damage at low initial stresses[33] and during a compressive dwell[74]. Therefore, Spindler [75, 76] proposed a revised approach, namely stress modified ductility:

εf=min⁡(εij, max⁡(εL, β0exp⁡(β1T)ε̇inβ2σβ3))(5)

where σ and ε̇inare the stress and inelastic strain rate, respectively. It is demonstrated that, for a wider range of stresses, the stress modified ductility exhaustion approach results in noteworthy better predictions of creep damage than both life fraction and R5-2003 approaches (see Fig. 1). This approach has recently been included into the latest R5 assessment procedure[16].

Some other creep rupture ductility models, including Evans-Wilshire model[77] (Eq. (6)), Anon model[46] (Eq. (7)) and Trunin-Golobova-Loginov model[78] (Eq. (8)), are listed below

ε f=min(ε U​,  max(ε L​,  exp(β 0+β 1σ +β 2T+β 3σ T))) (6)

ε f=min(ε U​,  max(ε L​,  exp(β 0+β 1T)σ β 2+β 3/T)) (7)

ε f=min(ε U​,  max(ε L​,  β 0Tβ 1σ β 2exp(β 3T+β 4σ T))) (8)

Payten et al.[79] conducted a statistical study on the existing ductility models by fitting them with the creep rupture data for P91 steel. Unfortunately, it was revealed that above-mentioned models (Eqs.(4), (5), (6), (7) and (8)) seemed not to be statistically robust enough, especially when experimental stress and temperature are highly correlated.

An alternative method to alleviate the statistical problem is to employ metallurgical variables in the ductility model. For instance, on the basis of Spindler's stress modified ductility model, Binda et al.[80] developed a model for 1CrMoV steel in the form of Eq. (9):

εf=min⁡(εU, max⁡(εL, β0exp⁡(β1T)ε̇inβ2σβ3f(MP)))(9)

where f(MP) is the overall material pedigree function, indicating that the creep rupture ductility is dependent not only on temperature, strain rate and stress, but also on chemical composition. With f(MP) function implemented in the ductility model, variance of the statistical results can be considerably improved by 54%. Note that burdensome work is required to quantify the influence of each chemical composition on the material pedigree function. Apart from that, Kimura et al.[71] argued that the significant difference in ductility cannot always be explained by a change in material pedigree and in precipitates. For instance, with decreasing stress, drastic drop in ductility for T23 steel at 550-650 ° C was observed but this is not the case for P23 steel, although these two steels had very similar chemical compositions[71]. One possible reason for the decline in ductility is the creep deformation concentration in a tiny recovered region formed at the vicinity of prior austenite grain boundary in the elastic stress regime. For some ductile austenitic alloys, it has been reported that ductility-dip cracking[81, 82, 83] occurring during the high temperature processing or welding may also deteriorate the ductility of metals at a certain temperature range. Nevertheless, the development of effective and rigorous analytical treatment of rupture ductility behavior is still underway. In consideration of the scattered nature of the ductility data, probabilistic treatment should be considered provided sufficient data are available.

3. Effect of Multiaxial States of Stress on the Creep Ductility
3.1. A literature survey of experimental data

Uniaxial creep tests have generated a large body of experimental data for the establishment of the basic dependence of creep ductility on some essential parameters, such as stress/strain rate, temperature and rupture time, as mentioned in Section 2. Nevertheless, most practical systems are inevitably experiencing a multiaxial stress state due to a change in geometry, material or loading condition. Thus, to provide a basis for describing the influence of the stress state on creep deformation and on rupture behavior of materials, for practical usage, multiaxial creep tests are increasingly being needed.

Since the circumferentially notched bar specimens are relatively less expensive and can generally be tested in the same machines used to collect standard uniaxial creep data, these axially loaded testpieces are widely used in multiaxial creep test. Fig. 7 shows the experimental creep ductility under multiaxial states of stress obtained by using round smooth bar (RSB) and round notched bar (RNB) specimens for CrMoV steel at 575 ° C[8], 9Cr-1Mo at 600 ° C[84], modified 9Cr-1Mo at 650 ° C[85], 2.25Cr1Mo at 550 ° C[86] and 600 ° C[87], Cr-Mo-V-Ti-B steel Durehete 1055 at 550 ° C[88], P92 at 650 ° C[89], C-Mn steel at 360 ° C[19], SS316H at 550 ° C[22, 90], SS321 at 600 ° C[91] and Inconel alloy 740 at 750 ° C[92]. As the axial strain is not uniform over the lengths of concern, the creep ductility of notched bar testpieces is usually defined by the reduction in area rather than the elongation. The multiaxial ductility factor and the stress triaxiality in Fig. 7 are given by the ratio of multiaxial ductility, εf* , to the uniaxial one, ε f, and the ratio of hydrostatic stress (mean normal stress), σ m, to the equivalent (von Mises) stress, σ e, respectively. Note that the stress triaxiality can be obtained from procedures in the European Code of Practice[93] or by using finite element analysis, focusing on the skeletal point or maximum damaged point in the plane of minimum section. Considering that creep cavities can neither nucleate nor grow under compressive stresses[94], stress triaxiality values less than zero will not be discussed in this paper. As can be seen in Fig. 7, an abundance of test data exhibits a monotonous decrease of the creep ductility with the increase of the triaxiality variable, for all the materials, at a given temperature. It is worthy to emphasize that the axially tensile tests on unnotched and notched bars are only able to generate ductility data in a high stress triaxiality range (σ m/σ e> 0.33) and there is a lack of data points in the range from 0 to 0.33. However, this low but positive triaxiality region is not uncommon in practical structures. To investigate the creep properties of materials over a wider range of multiaxial stress states, other specimen geometries and corresponding experimental data are required. It should be mentioned that there were also several examples of multiaxial specimens for creep testing such as thin-walled[95, 96] and thick walled tubes[97, 98, 99] subjected to tensile and torsion, cruciform specimens[100] subjected to axial forces, etc. Since different definitions of equivalent creep ductility were employed in different tests, these ductility data cannot be represented in Fig. 7.

Fig. 7. Effect of stress triaxiality on creep ductility for round smooth bar and round notched bar specimens at elevated temperatures.

The equivalent plastic strain at failure obtained from RNB specimens normalized by the uniaxial ductility for Weldox 420, Weldox 960[101] and API X65[102] at room temperature vs the stress triaxiality are plotted in Fig. 8. The use of average value of triaxiality over the equivalent plastic strain history causes the overall shift of data toward the right-hand side when compared with those in Fig. 7. As expected, the multiaxial ductility data obtained by ductile fracture tests of RNB specimens decrease monotonously with increasing triaxiality.Fig. 8 also plots data points by experiments on a butterfly specimen for steel A710[103] and round smooth/notch, dog-bone, flat, plate with a circular hole, pipe, flat-grooved and flat dog-bone tensile specimens for 2024-T351 aluminum[104]. Interestingly, one can see that the ductile fracture strain increases as triaxiality increases in the lower triaxiality regime. Experimental results from a double notched tube (DNT) specimen[101, 105] subjected to combined tension-torsion load for Weldox 420 and 960 have also verified that the equivalent plastic strain at failure is not necessary to be a monotonic decreasing function of stress triaxiality in a wide rage, which are not plotted in Fig. 8 for the sake of clarity. It has been reported that this phenomenon is mainly attributed to the change of fracture modes from void formation to shear band localization[106, 107]. Whether the slope discontinuity in the multiaxial ductility over a wide range of stress triaxiality is also valid for high temperature tests is still unknown and is a challenging question.

Fig. 8. Effect of stress triaxiality on equivalent plastic strain at failure for different specimen geometries at room temperature.

3.2. Modeling description

As mentioned in Section 3.1, the creep ductility exhibits great dependence on the multi-axial stress state. To date, various multiaxial ductility factor (MDF) models have been developed to describe the relation between the creep ductility and the stress triaxiality, and can be classified as follows: (1) Physically based MDF models; (2) Empirical MDF models; (3) Semi-empirical MDF models.

3.2.1. Physically based MDF models

The mechanism of creep fracture is commonly believed to be governed by the growth and coalescence of micro-voids typically at the grain boundaries (see Fig. 2), which is also the foundation of the existing physically based models that describe the multiaxial effect. The study was started by McClintock[49] in 1968, indicating the striking influence of stress triaxiality on the growth rate of long cylindrical holes in a perfectly plastic material. Based on McClintock's pioneering work, Rice and Tracey[50] considered the spherical holes in their study and found the exponential amplification of the plastic void growth rate by stress triaxiality. Hellan[108] demonstrated that this finding was also valid for void growth controlled by power-law creep. The multiaxial creep ductility model proposed by Rice and Tracey[50]could be expressed in the form of

εf* εf=exp⁡(12-3σm2σe)(10)

Based on a direct micromechanical calculation of grain-boundary cavity growth by power-law creep of the surrounding material, an approximate ductility model was presented by Cocks and Ashby[51] and could be expressed as

εf* εf=sinh⁡sinh23n-0.5n+0.5/sinh⁡[2(n-0.5n+0.5)σmσe](11)

where n is the steady-state creep exponent. The Cocks-Ashby model has been widely employed to calculate the creep ductility during the simulation of creep crack growth [18, 19, 20, 21, 22, 23, 25, 29, 69, 70] and to estimate the creep life of components[109, 110] subjected to triaxial stresses. However, it is argued that this model will strongly overestimate the creep ductility under some circumstances[111].

In order to overcome this problem, Wen and Tu[112] developed an alternative model that predicts cavity growth rates in better agreement with the theoretical solutions[51] by using the power-law creep controlled cavity growth theory. The multiaxial creep ductility factor could be given as

εf* εf=exp⁡exp23n-0.5n+0.5/exp⁡[2(n-0.5n+0.5)σmσe](12)

Regarding the diffusion-controlled cavity growth mechanism proposed by Hull and Rimmer[52], the influence of multiaxial stress state was considered by Spindler[113] in a simple form of

εf* εf=σeσ1(13)

Looking into the effect of the state of stress on the Dyson's constrained diffusion cavity growth model[114], Spindler[113] suggested another MDF model given by

εf* εf=2σe3(σ1-σm)(14)

3.2.2. Semi-empirical MDF models

Based on Rice-Tracey model (Eq. (10)), a semi-empirical ductility model considering the effect of multiaxial stress state on both cavity nucleation and growth was developed by Spindler[111] and expressed as

εf* εf=exp⁡[p1-σ1σe+q(12-3σm2σe)](15)

where p and q are material constants that can be obtained from fitting of Eq. (15) with experimental data. The typical values of p and q are 0.15 and 1.25, respectively, for Type 316 stainless steel (Spindler-II model) and 2.38 and 1.04, respectively, for Type 304 stainless steel (Spindler-II model). This model has already been included into the R5 guidelines [17].

An alternative semi-empirical model has been presented by Yatomi and Nikbin[115] on the basis of Cocks-Ashby model (Eq. (11)), which assumes (n-0.5)/(n+0.5) ≈3/2for most engineering materials:

εf* εf=0.610/sinh⁡[3σmσe](16)

3.2.3. Empirical MDF models

For annealed type 304 stainless steel at 593 ° C, Manjoine[116] suggested that the equivalent ductility is inversely proportional to the stress triaxiality:

εf* εf=σe3σm(17)

We will call it Manjoine-I model in this work. Another model (Manjoine-II model) for multiaxial ductility factor, which was concluded from the notched bar testing of various materials, has also been empirically presented by Manjoine[117].

εf* εf=2(1-3σmσe)(18)

3.2.4. Comparison of predictions by MDF models with experimental data

The predictions of the above-mentioned MDF models are shown as functions of the stress triaxiality in Fig. 7. Note that the creep exponent, n, is in the range from 7 to 15 for engineering alloys and the fluctuation of n within this range will have limited influence on the predicted results by the Cocks-Ashby model (Eq. (11)) and by the Wen-Tu model (Eq.(12)). Thus, n is assumed to be 10 in Fig. 7. Predictions by the Yatomi-Nikbin MDF (Eq.(16)) are not depicted because they are very close to those of the Cocks-Ashby model. It is also interesting to mention that the MDF for diffusion-controlled cavity growth (Eq. (13)), the MDF for constrained diffusion cavity growth (Eq. (14)) and the Spindler MDFs (Eq. (15)) can be re-expressed as functions of stress triaxiality only, σ m/σ e, by considering the axisymmetric tension conditions. Obviously, all the MDF models, except the Constrained MDF (Eq. (13)), exhibit a monotonous decline of the multiaxial ductility factor with increasing stress triaxiality. This feature is consistent with the overall trend of the experimental data. However, the Diffusion MDF (Eq. (14)) always overestimates the creep failure strain, which is not appropriate for use in a structural integrity assessment. The Spindler-II MDF model (Eq. (15) with p  = 2.38 and q   = 1.04) predicts values of the ductility agreeing well with the data from notched bar tension tests, e.g. for AISI 321 stainless steel at 600 ° C [91] and gives a lower bound of creep ductility. Within the region of σ m/σ e> 1/3, the other six MDF models (Eqs. (10), (11) and (12), (15) with p  = 0.15 and q  = 1.25; Eqs. (17) and (18)) provide quite similar predictions, which fit well the experimental data band.

The effect of stress biaxiality on creep ductility for type 316 and 304 austenitic stainless steel tested at 600 ° C and 593 ° C is illustrated in Fig. 9. Note that the stress biaxiality P2/P1is defined either as σ 3/σ 1 for σ 2=0 or σ 2/σ 1 for σ 3=0. The relationship between the stress biaxiality and stress triaxiality can be expressed as

σmσe=1+p2p13(1+p2p12-p2p1)(19)

Fig. 9. Effect of stress biaxiality on creep ductility for Type 316 and 304 stainless steels tested at 600 ° C and 593 ° C.

The test data were taken from Reference [111]. Since parameters in the Spindler-I and Spindler-II MDF models (Eq. (15)) were obtained by regression analysis of creep ductility data for type 316 and 304 steel, respectively, the coincidence of the model predictions with the corresponding data is expected. Both the diffusion-controlled cavity growth (Eq. (13)) and constrained cavity growth models (Eq. (14)) give non-conservative predictions when stress biaxiality is larger than zero, which once again prove that these two models are not suitable for assessing the creep life. It can also been seen from Fig. 9 that the Cocks-Ashby model (Eq. (11)) and the Manjoine-I model (Eq. (17)) will lead to infinite values for creep ductility as the stress biaxiality approaches the ratio minus unity, which is clearly not reasonable. Other MDF models including the Rice-Tracey model (Eq. (10)), the Wen-Tu model (Eq. (12)) and the Manjoine-II model (Eq. (18)) fairly well predict the behavior of type 316 steel over -1 <   P2/P1 <  1. It is interesting to note that the model proposed by Wen and Tu [112] is highly robust as it provides an excellent fit to the average values of multiaxial creep ductility data in both Fig. 7 and Fig. 9. Therefore, it is recommended to employ this model particularly when only limited multiaxial ductility data are available.

It should be pointed out that all the above-mentioned models are functions of the stress triaxiality, σ m/σ e, as the sole independent variable. However, a same stress triaxiality can result from multiple stress states with different principal stress values. Increasing amount of data obtained from the ductile fracture test[101, 103, 105, 106] for some metallic alloys at room temperature indicates that the ductility is not only dependent on the stress triaxiality, but also affected by the Lode parameter, L, related to the third deviatoric stress invariant, which is given by

L=2σ2-σ1-σ3σ1-σ3(20)

where σ 1, σ 2 and σ 3 are the principal stress components. A comparison of various ductility models in the 3D space of stress triaxiality, Lode angle and equivalent strain to fracture can be seen in Reference [118]. Due to the lack of necessary creep ductility data under multiaxial states of stress, this type of comprehensive MDF models used for a creep analysis have not been established yet.

3.3. Numerical methods to describe the effect of stress state

The effect of stress state on void growth and ductility can be illustrated in Fig. 10, with consideration of two initially identical cuboids containing a circular void in the center enclosed by dotted lines. Under uniaxial tension, a remarkable ductility will be obtained since the strain concentration diminishes with the void elongating in the direction of tension. Under triaxial stress state, on the other hand, very limited strain in three directions can only occur when additional volume is directly provided by a large growth of void since creep deformation is a constant-volume process. A change in magnitude or direction of the load will definitely change the deformation of the void and affect the ductility. Although several multiaxial creep tests have been conducted to reflect this process, it is very difficult or mostly impossible to observe in detail the effect of stress state covering a wide range by experimental techniques. Therefore, numerical simulations are required to solve this problem.

Fig. 10. Illustration of the effect of stress state on void growth and ductility (Δ luni and Δ ltri denote the elongation of the matrix under uniaxial and triaxial stress state, respectively).

An extensive amount of work has been carried out on void containing unit cells in order to get more insight in the stress-state-dependent mechanical behavior of the voided band undergoing general loading conditions in ductile fracture at room temperature, e.g. References [119, 120, 121], showing that the macroscopic deformation behavior of unit cells and the value of failure strain were strongly dependent on the value of the stress triaxiality. It has also been well concluded that the influence of the Lode parameter on the fracture strain is marginal in the sufficiently high stress triaxiality region but significant at moderate and low triaxialities[122, 123, 124, 125, 126]. For creep loading, although it is equally important and highly necessary, published literature is relatively limited. As one of the exceptions, finite element analyses of a representative material volume containing a void under different multiaxial stress states were conducted and a failure criterion related to a stress triaxiality dependent void volume fraction was proposed by Dennis[127]. Srivastava and Needleman[128] carried out detailed investigation on the effect of stress state on deformation and void growth in a creeping single crystal. Similar to the results for rate independent solids at room temperature, no remarkable effect of the Lode parameter was found at high values of the stress triaxiality. At low stress triaxialities, on the other hand, the void shape evolution and void volume fraction appeared to be significantly sensitive to the Lode parameter. Apart from that, it was found that the critical creep strain to failure (in terms of void coalescence) considerably reduces with an increasing value of Lode parameter from -1 to 1, for a given stress triaxiality equal to 1/3 and a given initial spacing of voids[129]. It is worthy to note that different values of ductility would be given by different assumptions on the failure criteria involving void coalescence and collapse[130, 131, 132, 133]. In addition, the applicability of numerical methods may be diminished by the lack of information on microscopic morphology and on underlying physics. Advanced observation techniques including X-ray computed tomography[134, 135] are believed to be helpful to improve the understanding of the entire process of void growth and coalescence, as well as to verify or modify the computational models.

4. Concluding Remarks

Due to its eminent importance in the strain-based approach, creep rupture ductility has been one of the focuses of continued research activities on elevated temperature strength design and structural integrity assessment over the last decades. This paper has concisely reviewed the effects of stress level and stress state on creep ductility. The main conclusions are summarized as follows:

(1) The uniaxial creep ductility data for engineering alloys may vary in a complex manner over a wide range of the stress level and can generally be divided into three regimes[47], i.e. an upper plateau associated with viscoplastic cavity growth at high strain rates, a lower plateau governed by constrained diffusion cavity growth at low strain rates, and transition region where diffusion-controlled cavity growth prevails.

(2) The existing empirical ductility models can generally describe the variation of uniaxial creep ductility with temperature, stress and/or strain rate. A metallurgical-variable modified ductility model seemed to show best match with test data from the viewpoint of statistics. Nevertheless, none of them is completely satisfactory.

(3) An abundance of experimental data collected from round smooth bar and round notched bar tension tests exhibits a monotonous decrease of the creep ductility with increasing stress triaxiality for all the materials at a given temperature. Other types of specimens and corresponding tests are required to characterize the multiaxial creep ductility at low but positive values of triaxiality variable.

(4) Several multiaxial ductility factor models including the Cocks-Ashby model, the diffusion model, the constrained model and the Manjoine-I model may give rise to non-conservative predictions under some circumstances, which are not appropriate for use in a structural integrity assessment. The Wen-Tu model is highly robust and excellently fit the average values of multiaxial creep ductility. The existing MDF models at elevated temperatures have not incorporated the influence of Lode parameter and should be improved in the future.

(5) Numerical analyses of void containing unit cells show that the critical failure strain strongly depend on the value of the stress triaxiality at high triaxialities, and the effect of Lode parameter appears to be pronounced at low triaxialities. Adequate attention should be paid to the use of assumptions made in the failure criteria.

It is worthy to mention that this paper only addresses the creep ductility of the base metal. Our earlier work[136, 137] suggested that the creep damage occurred frequently in weldments, in particular in the heat affected zone, which should be further investigated in the context of stress level and stress state in the near future.

Acknowledgements Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant Nos.11472105 and 51505149) and the “111 project”. The first author wishes to thank the financial support provided by Shanghai Sailing Program (Grant No. 15YF1402900). Careful check conducted by Dr. Imran Khan at Bhabha Atomic Research Centre is also greatly appreciated.

The authors have declared that no competing interests exist.

Reference
[1] R. Viswanathan, J. Stringer. J. Eng. Mater, 122(2000), pp. 246-255 [Cited within:1]
[2] E. Robinson. Trans. ASME, 60(1938), pp. 253-259 [Cited within:1]
[3] 2013 ASME Boiler, Pressure Vessel Code. Section III: Rules for Construction of Nuclear Facility Components, Division 1- Subsection NH, Class 1 Components in Elevated Temperature Service. American Society of Mechanical Engineering, New York, USA (2013) [Cited within:1]
[4] RCC-MRx. Design and Construction Rules for Mechanical Components in High-Temperature Structures, Experimental Reactors and Fusion Reactors. AFCEN, Paris, France (2012) [Cited within:1]
[5] BS7910: 2013. Guidance to Methods for Assessing the Acceptability of Flaws in Metallic Structures. British Stand ards Institution, London, UK (2013) [Cited within:1]
[6] R. Viswanathan. Damage Mechanisms and Life Assessment of High Temperature Components. ASM International, Materials Park (1989) [Cited within:1]
[7] M. W. Spindler. Mater. Sci. Technol, 23(2007), pp. 1461-1470 [Cited within:2]
[8] N. Isobe, K. Yashirodai, K. Murata. Eng. Fract. Mech, 123(2014), pp. 211-222 [Cited within:2]
[9] L. M. Kachanov. Int. J. Fract, 97(1999), pp. 11-18 [Cited within:1]
[10] D. R. Hayhurst. J. Mech. Phys. Solids, 20(1972), pp. 381-382 [Cited within:1]
[11] D. R. Hayhurst, P. R. Brown, C. J. Morrison. Philos. Trans. R. Soc. London Ser. A, 311(1984), pp. 131-158 [Cited within:1]
[12] D. R. Hayhurst, P. R. Dimmer, C. J. Morrison. Philos. Trans. R. Soc. London Ser. A, 311(1984), pp. 103-129 [Cited within:1]
[13] C. J. Hyde, T. H. Hyde, W. Sun, A. A. Becker. Eng. Fract. Mech, 77(2010), pp. 2385-2402 [Cited within:1]
[14] R. K. Penny, D. L. Marriott. Design for Creep. (2nd ed. )Chapman & Hall, London (1995) [Cited within:1]
[15] T. H. Hyde, M. Saber, W. Sun. Int. J. Press. Ves. Pip, 87(2010), pp. 721-729 [Cited within:1]
[16] R5. Assessment Procedure for the High Temperature Response of Structures, year 3, Revision 002. EDF Energy, Gloucester, UK (2014) [Cited within:2]
[17] R5. Assessment Procedure for the High Temperature Response of Structures, year 3. British Energy Generation Ltd, Gloucester, UK (2003) [Cited within:3]
[18] M. Yatomi, K. M. Nikbin, N. P. O'Dowd. Int. J. Press. Ves. Pip, 80(2003), pp. 573-583 [Cited within:2]
[19] M. Yatomi, A. D. Bettinson, N. P. O'Dowd, K. M. Nikbin. Fatigue Fract. Eng. Mater. Struct, 27(2004), pp. 283-295 [Cited within:3]
[20] M. Yatomi, N. P. O'Dowd, K. M. Nikbin, G. A. Webster. Eng. Fract. Mech, 73(2006), pp. 1158-1175 [Cited within:2]
[21] M. Yatomi, C. M. Davies, K. M. Nikbin. Eng. Fract. Mech, 75(2008), pp. 5140-5150 [Cited within:2]
[22] C. S. Oh, N. H. Kim, Y. J. Kim, C. M. Davies, K. Nikbin, D. W. Dean. Eng. Fract. Mech, 78(2011), pp. 2966-2977 [Cited within:3]
[23] N. H. Kim, C. S. Oh, Y. J. Kim, C. M. Davies, K. Nikbin, D. W. Dean. Eng. Fract. Mech, 105(2013), pp. 169-181 [Cited within:2]
[24] J. F. Wen, S. T. Tu, X. L. Gao, J. N. Reddy. Eng. Fract. Mech, 98(2013), pp. 169-184 [Cited within:1]
[25] M. Yatomi, M. Tabuchi. Eng. Fract. Mech, 77(2010), pp. 3043-3052 [Cited within:2]
[26] J. F. Wen, S. T. Tu, X. L. Gao, J. N. Reddy. Mater. Sci. Technol, 30(2014), pp. 32-37 [Cited within:1]
[27] R. Sand ström, R. Wu. J. Nucl. Mater, 441(2013), pp. 364-371 [Cited within:1]
[28] R. Wu, R. Sand ström, L. Z. Jin. Mater. Sci. Eng. A, 583(2013), pp. 151-160 [Cited within:1]
[29] M. Pettinà, F. Biglari, A. Heaton, P. Brown, K. Nikbin. J. Eur. Ceram. Soc, 34(2014), pp. 2799-2805 [Cited within:2]
[30] S. Y. Zamrik, D. C. Davis. J. Press. Ves. -T. ASME, 113(1991), pp. 180-186 [Cited within:1]
[31] Y. Takahashi. Int. J. Pres. Ves. Pip, 85(2008), pp. 406-422 [Cited within:1]
[32] M. W. Spindler, G. Knowles, S. Jacques, C. Austin. Mater. High Temp, 31(2014), pp. 284-304 [Cited within:1]
[33] M. W. Spindler. Improved Methods for the Calculation of Creep Damage. British Energy Generation Limited, Gloucester, UK (2009) [Cited within:2]
[34] X. L. Yan, X. C. Zhang, S. T. Tu, S. L. Mannan, F. Z. Xuan, Y. C. Lin. Int. J. Pres. Ves. Pip, 126(2015), pp. 17-28 [Cited within:1]
[35] K. Wasmer. Prediction of creep crack growth in a range of steels
PhD Thesis; Imperial College London (2003) [Cited within:1]
[36] J. O. Stiegler, K. Farrell, B. T. M. Loh, H. E. McCoy. Trans ASM Quart, 60(1967), pp. 494-503 [Cited within:1]
[37] T. H. Courtney. Mechanical Behavior of Materials. Waveland Press, Long Grove(2005) [Cited within:1]
[38] K. Ankit, N. Prasad. Mater. Sci. Eng. A, 528(2011), pp. 4209-4216 [Cited within:1]
[39] M. Götting, J. Rösler. Comput. Struct, 85(2007), pp. 225-232 [Cited within:1]
[40] R. Raj, M. Ashby. ActaMetall, 23(1975), pp. 653-666 [Cited within:1]
[41] H. Riedel. ActaMetall, 32(1984), pp. 313-321 [Cited within:1]
[42] B. Dyson. Scr. Metall, 17(1983), pp. 31-37 [Cited within:1]
[43] M. E. Kassner. Fundamentals of Creep in Metals and Alloys. Butterworth-Heinemann, Oxford (2015) [Cited within:1]
[44] National Institute for Materials Science. Creep data sheet. http://smds.nims.go.jp/creep/index_en.html (2016 [Cited within:2]
[45] S. Holdsworth. J. Press. Ves. -T. ASME, 130(2008), p. 024001 [Cited within:1]
[46] S. Holdsworth. Mater. High Temp, 21(2004), pp. 25-31 [Cited within:2]
[47] R. Hales. Fatigue Fract. Eng. Mater. Struct, 17(1994), pp. 579-591 [Cited within:2]
[48] J. Hancock. Met. Sci, 10(1976), pp. 319-325 [Cited within:1]
[49] F. A. McClintock. Mater. High Temp, 35(1968), pp. 363-371 [Cited within:2]
[50] J. Rice, D. M. Tracey. J. Mech. Phys. Solids, 17(1969), pp. 201-217 [Cited within:3]
[51] A. F. Cocks, M. F. Ashby. Met. Sci, 8(1980), pp. 395-402 [Cited within:3]
[52] D. Hull, D. Rimmer. Philos. Mag, 4(1959), pp. 673-687 [Cited within:2]
[53] M. Speight, W. Beere. Met. Sci, 9(1975), pp. 190-191 [Cited within:1]
[54] B. Dyson. Met. Sci, 10(1976), pp. 349-353 [Cited within:1]
[55] J. Rice. ActaMetall, 29(1981), pp. 675-681 [Cited within:1]
[56] V. Tvergaard. J. Mech. Phys. Solids, 32(1984), pp. 373-393 [Cited within:1]
[57] T. Delph. Metall. Mater. Trans. A, 33(2002), pp. 383-390 [Cited within:1]
[58] H. Riedel. Fracture at High Temperatures. Springer-Verlag, Berlin (1987) [Cited within:1]
[59] A. Needleman, J. Rice. ActaMetall, 28(1980), pp. 1315-1332 [Cited within:1]
[60] M. Kassner, T. Hayes. Int. J. Plasticity, 19(2003), pp. 1715-1748 [Cited within:1]
[61] J. Lin, Y. Liu, T. Dean. Int. J. Damage. Mech, 14(2005), pp. 299-319 [Cited within:1]
[62] A. Cocks, M. Ashby. Prog. Mater. Sci, 27(1982), pp. 189-244 [Cited within:1]
[63] M. W. Spindler. The Development of Improved Methods for the Calculation of Creep Damage in Type 316H Steel. British Energy Generation Limited, Gloucester, UK (2003) [Cited within:1]
[64] A. Mehmanparast, C. Davies, G. Webster, K. Nikbin. Mater. High Temp, 31(2014), pp. 84-94 [Cited within:2]
[65] A. Mehmanparast. The influence of inelastic damage on creep, fatigue and fracture toughness. PhD Thesis; Imperial College London (2012) [Cited within:2]
[66] A. Mehmanparast. Int. J. Pres. Ves. Pip, 120-121(2014), pp. 55-65 [Cited within:1]
[67] J. P. Tan, S. T. Tu, G. Z. Wang, F. Z. Xuan. Eng. Fract. Mech, 99(2013), pp. 324-334 [Cited within:1]
[68] J. P. Tan, G. Z. Wang, F. Z. Xuan, S. T. Tu. Acta Metall. Sin. (Engl. Lett. ), 24(2011), pp. 81-91 [Cited within:1]
[69] J. W. Zhang, G. Z. Wang, F. Z. Xuan, S. T. Tu. Mater. Design, 65(2015), pp. 644-651 [Cited within:2]
[70] J. W. Zhang, G. Z. Wang, F. Z. Xuan, S. T. Tu. Mater. High Temp, 32(2015), pp. 369-376 [Cited within:2]
[71] K. Kimura, K. Sawada, H. Kushima. J. Press. Ves. -T. ASME, 134(2012), p. 031403 [Cited within:4]
[72] K. Kimura, K. Sawada, K. Kubo, H. Kushima. In Proc. ASME/JSME 2004 Pressure Vessels and Piping Conference. San Diego, USA(2004), pp. 11-18 [Cited within:1]
[73] R. Viswanathan. ASTM J. Test. Eval, 3(1975), pp. 93-106 [Cited within:1]
[74] M. W. Spindler, W. M. Payten. J. ASTM Int, 8 (2011) Paper ID JAI103806 [Cited within:1]
[75] M. Spindler. Int. J. Press. Ves. Pip, 82(2005), pp. 175-184 [Cited within:1]
[76] M. Spindler. Int. J. Press. Ves. Pip, 82(2005), pp. 185-194 [Cited within:1]
[77] R. W. Evans, B. Wilshire. Creep of Metals and Alloys. The Institute of Metals, London (1985) [Cited within:1]
[78] I. Trunin, N. G. Golobova, E. A. Loginov. In: Proc. Fourth International Symposium on Heat Resistant Metallic Materials. MaláFatra, Czechoslovak Socialist Republic (1971), p. 168 [Cited within:1]
[79] W. M. Payten, D. Dean, K. U. Snowden. Mater. Design, 33(2012), pp. 491-495 [Cited within:1]
[80] L. Binda, S. R. Holdsworth, E. Mazza. Int. J. Press. Ves. Pip, 87(2010), pp. 319-325 [Cited within:1]
[81] W. L. Mo, X. B. Hu, S. P. Lu, D. Z. Li, Y. Li. J. Mater. Sci. Technol, 31(2015), pp. 1258-1267 [Cited within:1]
[82] A. J. Ramirez, J. C. Lippold. Mater. Sci. Eng. A, 380(2004), pp. 259-271 [Cited within:1]
[83] A. J. Ramirez, J. C. Lippold. Mater. Sci. Eng. A, 380(2004), pp. 245-258 [Cited within:1]
[84] S. Goyal, K. Laha, C. R. Das, S. Panneerselvi, M. D. Mathew. Metall. Mater. Trans. A, 45(2014), pp. 619-632 [Cited within:1]
[85] K. Yoshida, M. Yatomi. Proc. Eng, 10(2011), pp. 490-495 [Cited within:1]
[86] O. Kwon, A. J. Tack, C. W. Thomas, S. Swann. Int. J. Press. Ves. Pip, 77(2000), pp. 91-97 [Cited within:1]
[87] S. Goyal, K. Laha, C. R. Das, S. Panneerselvi, M. D. Mathew. Int. J. Mech. Sci, 75(2013), pp. 233-243 [Cited within:1]
[88] O. Kwon, C. W. Thomas, D. Knowles. Int. J. Press. Ves. Pip, 81(2004), pp. 535-542 [Cited within:1]
[89] Y. Chang, H. Xu, Y. Ni, X. Lan, H. Li. Mater. Sci. Eng. A, 636(2015), pp. 70-76 [Cited within:1]
[90] A. D. Bettinson. The influence of constraint on the creep crack growth of 316h stainless steel. PhD Thesis; Imperial College London (2001) [Cited within:1]
[91] L. Allais, Q. Auzoux, M. Reytier, A. Pineau. Méca. Ind, 6(2005), pp. 45-54 [Cited within:2]
[92] J. P. Shingledecker, G. M. Pharr. Metall. Mater. Trans. A, 43(2012), pp. 1902-1910 [Cited within:1]
[93] G. A. Webster, S. Holdsworth, M. Loveday, K. Nikbin, I. Perrin, H. Purper, R. Skelton, M. Spindler. Fatigue Fract. Eng. Mater. Struct, 27(2004), pp. 319-342 [Cited within:1]
[94] M. W. Spindler. A Revised Approach for the Assessment of Creep-Fatigue Cycles with Compressive Dwells. British Energy Generation Limited, Gloucester, UK (2001) [Cited within:1]
[95] P. Delobelle, F. Trivaudey, C. Oytana. Nucl. Eng. Des, 114(1989), pp. 365-377 [Cited within:1]
[96] Z. Kowalewski. Arch. Mech, 47(1995), pp. 13-26 [Cited within:1]
[97] J. Henderson. High Temp. Technol, 8(1990), pp. 243-251 [Cited within:1]
[98] L. B. Niu, M. Kobayashi, H. Takaku. ISIJ Int, 42(2002), pp. 1156-1161 [Cited within:1]
[99] L. B. Niu, A. Katsuta, M. Kobayashi, H. Takaku. ISIJ Int, 43(2003), pp. 251-255 [Cited within:1]
[100] M. Sakane, H. Tokura. Int. J. Damage. Mech, 11(2002), pp. 247-262 [Cited within:1]
[101] J. Faleskog, I. Barsoum. Int. J. Solids Struct, 50(2013), pp. 4241-4257 [Cited within:3]
[102] C. S. Oh, N. H. Kim, Y. J. Kim, J. H. Baek, Y. P. Kim, W. S. Kim. Eng. Fract. Mech, 78(2011), pp. 124-137 [Cited within:1]
[103] T. Wierzbicki, Y. B. Bao, Y. L. Bai. In: Proc. 2005 SEM Annual Conference and Exposition on Experimental and Applied Mechanics. Portland , USA(2005), pp. 1295-1303 [Cited within:2]
[104] T. Wierzbicki, Y. Bao, Y. -W. Lee, Y. Bai. Int. J. Mech. Sci, 47(2005), pp. 719-743 [Cited within:1]
[105] I. Barsoum, J. Faleskog. Int. J. Solids Struct, 44(2007), pp. 1768-1786 [Cited within:2]
[106] Y. Bao, T. Wierzbicki. Int. J. Mech. Sci, 46(2004), pp. 81-98 [Cited within:2]
[107] M. Brünig, D. Brenner, S. Gerke. Eng. Fract. Mech, 141(2015), pp. 152-169 [Cited within:1]
[108] K. Hellan. Int. J. Mech. Sci, 17(1975), pp. 369-374 [Cited within:1]
[109] C. H. Richter. Comput. Struct, 81(2003), pp. 919-927 [Cited within:1]
[110] G. Horseman. Energy Mater. : Mater. Sci. Eng. Energy Syst, 4(2012), pp. 213-237 [Cited within:1]
[111] M. W. Spindler. Fatigue Fract. Eng. Mater. Struct, 27(2004), pp. 273-281 [Cited within:3]
[112] J. F. Wen, S. T. Tu. Eng. Fract. Mech, 123(2014), pp. 197-210 [Cited within:2]
[113] M. W. Spindler. Mater. High Temp, 21(2004), pp. 47-52 [Cited within:2]
[114] B. Dyson. Can. Metall. Quart, 18(1979), pp. 31-38 [Cited within:1]
[115] M. Yatomi, K. M. Nikbin. Mater. High Temp, 31(2014), pp. 141-147 [Cited within:1]
[116] M. J. Manjoine. J. Eng. Mater, 97(1975), pp. 156-161 [Cited within:1]
[117] M. J. Manjoine. Weld J. , 61(1982), pp. 50-57 [Cited within:1]
[118] Y. Bai, T. Wierzbicki. Eng. Fract. Mech, 135(2015), pp. 147-167 [Cited within:1]
[119] A. Needleman. J. Appl. Mech, 39(1972), pp. 964-970 [Cited within:1]
[120] M. Worswick, R. Pick. J. Mech. Phys. Solids, 38(1990), pp. 601-625 [Cited within:1]