For computing transverse properties, RVEs of 50 µ m ×  50 µ m with three different fibre volume fractions: 33.73%, 42.92%, and 51.11%, were created, as shown in Fig. 1.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. RVEs of 50 µ m ×  50 µ m with three different fibre volume fractions: 33.73% (a), 42.92% (b), and 51.11% (c), for modelling the transverse properties.

For each fibre volume fraction, RVEs of five different void contents are created. The voids are introduced to the matrix randomly. Only intra-tow voids are considered and their sizes are limited by the inter-fibre distances. The actual void content is determined by the area of RVE. As an example, the maximum void content is 17.64% for V_f  = 42.92%, as shown inFig. 2.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Maximum void content of 17.64% for Vf  = 42.92%.

In this study, the void content, V_v, is defined to be with respect to the matrix only. The void content with respect to the composite is defined as the net void content, V_vn, which is related to V_v by

V_vn=(1-V_f)V_v(1)

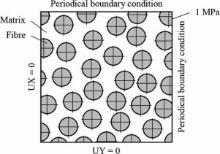
PLANE183 element is used with the option of plane strain. As shown in Fig. 3, the horizontal and vertical displacements are constrained for the left and bottom edges, respectively. Periodical boundary conditions are applied to the right and top edges. A unit tensile stress (p₀  = 1 MPa) was applied at the right edge.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Boundary conditions for transverse properties.

The x- and y- displacements of the RVE, δ _x and δ _y, are used for deriving the effective transverse modulus and transverse-transverse Poisson's ratio.

(2)

(3)

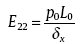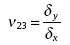where L₀ is the size of the RVE (50 µ m). In addition to deformation, the distribution of stress, σ _xxmax, was obtained from FEA. When the fibre volume fraction is 42.92%, the distributions of σ _xxmax with no voids and maximum voids are shown in Fig. 4. It is shown that high stress is induced around fibres. When voids are introduced, higher stress concentrations occur in the matrix around the voids.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Normal stress due to tensile load for transverse RVEs of 42.92% fibre volume fraction with no voids (a) and maximum voids (b).

Similar to computing the transverse properties, RVEs of 50 µ m ×  50 µ m with three different fibre volume fractions, 33.73%, 42.92%, and 51.11%, are created for the modelling of the longitudinal properties. Similarly, for each fibre volume fractions, RVEs of five different void contents are created. The voids are introduced to the matrix randomly. The x- and y- displacements of each RVE, δ _x and δ _y, are used for deriving the effective longitudinal modulus and longitudinal-transverse Poisson's ratio.

In order to take into account the voids, homogenisation was carried out for the matrix and voids. The effective modulus of the matrix with voids was predicted using Kerner model, which reads

Eme=9KmeGme3Kme+Gme(4)

where

Gme=Gm7-5υm1-Vv7-5υm+(8-10υm)Vv(5)

Kme=4GmKm(1-Vv)4Gm+3VvKm(6)

υm=3Kme-2Gme2(Gme+3Km)(7)

These equations coincide numerically with the corresponding lower bounds of Hashin's sphere assemblage model.

The effective modulus of resin is used for calculating the properties of a composite with voids. In general, longitudinal modulus can be predicted using the rule of mixtures (RoM) with good accuracy, i.e.

E₁₁=E_fLV_f+E_me  (1-V_f) (8)

Likewise, the Poisson's ratio is given by

ν ₁₂=ν _fLTV_f+ν _me  (1-V_f) (9)

For transverse modulus, many models have been developed. In this study, Hashin's CCM was chosen. For a two phase composite material, the transverse modulus is given by

(10)

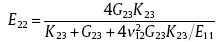where

G23=Gme[1+Vf(1+Cm)C3-Vf[1+3Cm21-Vf2/(1+C2Vf3)]](11)

K23=Vf1Kfit-KmTTe+1-VfKmTTe+Gme+KmTTe(12)

Kf=EfT21-υfiT-2υfiT+EfT/EfL(13)

KfTT=GfTT3+Kf(14)

Kme=Eme31-2υme(15)

KmTTe=Gme3+Kme(16)

c_f, c_m, c₁, c₂ and c₃ are constants, given by

Cf=KfTTKfTT+2GfTT(17)

Cm=KmTTeKmTTe+2Gme=13-4υm(18)

Cl=GfTTGme(19)

(20)

C3=C1+CmC1-1(21)

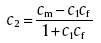The transverse-transverse Poisson's ratio is given by

υ23=E222G23-1(22)

The in-plane shear modulus is given by

G12=Gme1-VfGme+1+VfGf1-VfGf+1+VfGme(23)

The elastic properties were also modelled using the Mori-Tanaka method^{[27, 28]} based on Eshelby's inclusion theory^[29] and Mori-Tanaka's mean field theory^[30]. Using the Mori-Tanaka method, the effective composite modulus is given by

C=[(1-V_f)C_m+V_fC_fA][(1-V_f)I+V_fA]^-1(24)

A=[1+SCm-1(Cf-Cm)]-1(25)

where C_f and C_m are the elastic stiffness tensors for the matrix and fibres, respectively; Ais the concentration factor relating the average strain in the effective reinforcement to that of the unknown effective material in which it is embedded; and S is the Eshelby tensor.

It is seen from Eqs. ((4), (5), (6) and (7)) that the modulus of the matrix decreases with increasing void content. An approximate linear relationship is found. For the epoxy used in this study, the normalised matrix modulus when voids are present is given by

(26)

Eq. (26) shows that a 1% increase in void content will cause a 1.76% decrease in the matrix modulus.

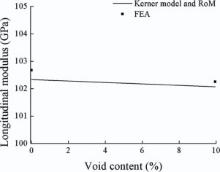
The matrix modulus from Eq. (26) can be used for calculating the lamina properties. The longitudinal moduli from the FEA and Kerner-RoM approach are shown in Fig. 5. It is shown that the RoM can well predict the longitudinal modulus, and voids have little effect on the longitudinal properties. For example, when the fibre volume fraction is 42.92%, a 1% increase in void content will only cause a 0.04% decrease in the matrix modulus.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Longitudinal moduli from the FEA predictions and the analytical approach.

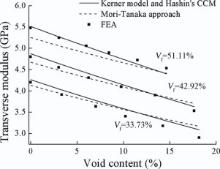
The transverse moduli from the FEA and two analytical approaches, i.e. Kerner-Hashin and Mori-Tanaka, are shown in Fig. 6. It is shown that good agreement is found between Kerner-Hashin approach, Mori-Tanaka method and FEA.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Transverse moduli from the FEA and two analytical approaches.

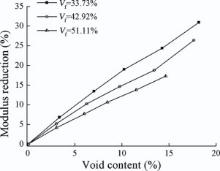
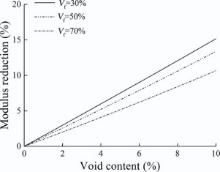
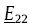
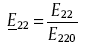The transverse modulus reduction caused by voids is shown in Fig. 7. It is shown that approximate linear relationships exist, with the slope decreasing with increasing fibre volume fraction. On average, every 1% increase in the void content results in 1.5% decrease in the transverse modulus. For any given fibre volume fraction, for convenience, the relative transverse modulus, , is defined as

(27)

where E₂₂₀ is the void-free transverse modulus. The relative transverse modulus is then given by

(28)

As aforementioned, k is the slope which is dependent on fibre volume fraction. A regression model can be fitted to the slope data. Thus, the relative transverse modulus is given by

(29)

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Transverse modulus reduction vs. void content.

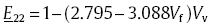The in-plane shear modulus is obtained using the Kerner-Hashin approach. According to Eq. (5), the normalised shear modulus of the matrix when voids are present is given by

(30)

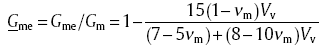When the void content is low, Eq. (30) can be approximated by a linear regression model, as given by

(31)

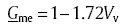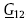
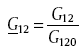The in-plane shear modulus of the composite can then be calculated using Eq. (23). The in-plane shear modulus decreases with increasing void content. At low void content, linear relationships can be assumed. Likewise, the relative in-plane shear modulus, , is defined as

(32)

where G₁₂₀ is the void-free in-plane shear modulus. The in-plane shear modulus reduction caused by voids is shown in Fig. 8. A regression model can be fitted to the data:

(33)

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. In-plane shear modulus reduction vs. void content.

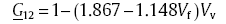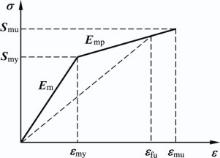
In general, fibres exhibit elastic behaviour, but yielding must be taken into account for the matrix. If the fibres have higher failure strain than the matrix, e.g. glass, yield of the matrix needs to be considered. In this study, a bilinear relationship as shown in Fig. 9 is used to describe the stress-strain relationship for the epoxy.

Fig. 9.

	Figure Option ViewDownloadNew Window
	Fig. 9. Bilinear stress-strain relationship for epoxy.

It is shown from an experimental study^[31] that ε _mu is approximately 4%. The yield strength is empirically determined to be S_my≈ 0.75S_mu. The yield strain is then ε _my≈ 0.75S_mu/E_m. The modulus of the epoxy in the plastic region is then E_mp=0.25S_mu/(ε _mu-ε _my). If the fibres fail before the ultimate strain of the epoxy, the effective modulus of the epoxy is given by

Eme=0.75εmu+0.25εfu-εmyεfu(εmu-εmy)Smu(34)

If the epoxy fails before the fibres, the effective modulus for the epoxy is then E_me=S_mu/ε _mu. E_me can be used in the micromechanical modelling for deriving the lamina properties. The longitudinal tensile strength is given by

S_Lt=E₁₁ε _mu(35)

On the other hand, if the fibres have lower failure strain than the matrix, e.g. carbon, the possible failure mode is fibre breakage, and the longitudinal strength can be simply calculated using the effective modulus and fibre failure strain, e.g. 1.65% for AS4 graphite fibres, i.e.

S_Lt=E₁₁ε _fu(36)

It is seen the modulus of the matrix decreases with increasing void content. However, because the fibres have much higher modulus, only a slight decrease in the longitudinal strength occurs with increasing void content, and this confirms that voids have little effect on the longitudinal properties.

It is well known that the transverse tensile strength is more complex than the longitudinal one, and is affected by many factors including interfacial bonding, fibre distribution, and voids. In general, the transverse strength is less than that of the unreinforced matrix. The consequence is that the transverse plies in a cross-ply laminate usually start to crack before the parallel ones^[32].

It is shown from the FEA predictions that the introduction of fibres to the matrix increases the maximum stress of stress concentration. It is postulated that the increased stress concentration will reduce the strength. Thus, the transverse strength is related to the maximum stress from FEA as given by

STt0=cSmσxxnomσxxmax0(37)

where S_Tt0 is the void-free transverse tensile strength; c is a constant; σ _xxnom is the nominal stress being applied; and σ _xxmax0 is the maximum stress in the void-free composite. The introduction of c is due to the fact that localised high stress has limited effect on strength decrease ^[8].

A model for predicting the transverse strength of a fibre reinforced composite is given by^[1]

STt=SmKσ(38)

where Kσ=1-Vf(1-Em/Ef)1-(4Vf/π)1/2(1-Em/Ef), representing the maximum stress concentration in the matrix in which fibres are arranged in a square array. Similar to the FEA predictions, Eq. (38) also indicates that the transverse tensile strength is dependent on the maximum stress concentration.

In this study, the tensile strength of the matrix was determined to be 55 MPa from experiments. It is found when c  = 1.5, the transverse strengths from FEA prediction are in good agreement with those obtained using Eq. (38), as shown in Fig. 10. This can be well explained by Weibull theory.

Fig. 10.

	Figure Option ViewDownloadNew Window
	Fig. 10. Transverse strengths from FEA prediction and analytical model.

The presence of voids in the matrix increases the maximum stress and consequently reduces the transverse strength. Similar to Eq. (37), the strength with voids is given by

STt=cSTt0σxxmax0σxxmax(39)

where σ _xxmax is the maximum stress when voids are present. The same constant c is used.

For convenience, the ratio of the transverse strength when voids are present and the void free transverse strength is defined as the relative transverse strength, S¯Tt, i.e.

(40)

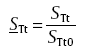The relative strength can be expressed by the following formula^[18].

(41)

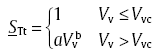The critical void content was empirically determined to be 2% from the FEA data. For the three fibre volume fractions being studied, the regression formulas are given by

(42)

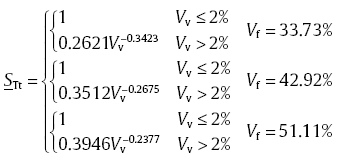Eq. (42) can be summarised to

(43)

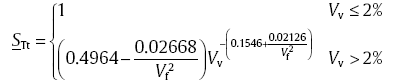A comparison of the relative transverse strengths from the FEA predictions and the regression model is given in Fig. 11, which has proven the validity of the developed regression model.

Fig. 11.

	Figure Option ViewDownloadNew Window
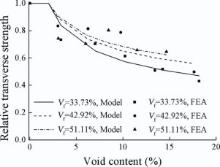	Fig. 11. Relative transverse strengths from the FEA predictions and the regression model.

The longitudinal compressive strength is dependent on the failure mode. The possible compressive failure modes include pure compression, delamination/shear, and microbuckling or kinking. When voids are present, no models are available for the longitudinal compressive strength. However, since the compressive strength and transverse tensile strength are both matrix-dominated properties, voids have large effect, and in this study, the model developed for the relative transverse tensile strength in Eq. (43)is used for finding the longitudinal compressive strength when voids are present.

In transverse compressive loading, the failure is initiated by fibre-matrix debonding. The transverse compressive modulus is higher than the matrix modulus and is close to the transverse tensile modulus. The transverse compressive strength is found to be nearly independent of fibre volume fraction^[33]. This type of failure is expected at an applied normal stress of about two times the in-plane shear strength, on planes inclined at 45° to the loading direction and parallel to the fibreaxis^[32]. Likewise, the transverse compressive strength is a matrix-dominated property. Thus, Eq. (43) is used for finding the transverse compressive strength when voids are present.

It is expected, unless for very high fibre volume fractions, the in-plane shear strength is close to the shear strength of the matrix^{[32, 34]}. The shear strength of commonly used resins, e.g. epoxy is normally higher than the tensile strength. Experimental data show that the in-plane shear strength can be between 2 and 2.5 times the transverse tensile strength ^[32]. Since shear strength is also matrix-dominated, when voids are present, the model developed for the relative transverse tensile strength in Eq. (43) is also used to obtain the shear strength.

Guo et al.^[16] studied the effects of voids on the tensile strength of T700/TDE85 carbon fibre reinforced epoxy composites. The nominal fibre volume fraction was 60% and the stacking sequence was [0/90]_3S. For this type of carbon fibre reinforced composites, the transverse plies are more sensitive to voids and will fail before the longitudinal plies. After the failure of the transverse plies, the laminate will fail catastrophically because of the lack of load transfer. When deriving the tensile strength, the transverse modulus and strength are first derived using Eqs. (12), (31), (38) and (45). The strain to failure can be calculated accordingly, and this will be the strain to failure. The effective stiffness of the laminate is calculated using the RoM. Using the calculated strain to failure and effective stiffness, the tensile strength is calculated. The calculated relative tensile strength and the experimental results are shown in Fig. 12, from which it is seen that good agreement exists.

Fig. 12.

	Figure Option ViewDownloadNew Window
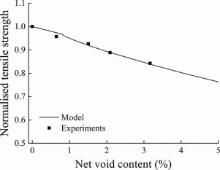	Fig. 12. Tensile strengths from model and experiments.

Zhang et al.^[15] studied composites made from woven-fabric carbon/epoxy prepregs (T300/914). The stacking sequence was [(± 45)₄/(0, 90)/(± 45)₂]_S. Three different porosity levels ranging from 0.33% to 1.50% were obtained by implementing different magnitudes of autoclave pressures.

For a laminate of general stacking sequences, the effective stiffness of each lamina needs to be derived. For a lamina of θ angle, the effective stiffness can be given by ^[35]

E_θ =E₂₂+(E₁₁-E₂₂)cos⁴θ (44)

For ± 45 laminas, the effective stiffness is then E_{± 45}=(E₁₁+3E₂₂)/4. For this [(± 45)₄/(0, 90)/(± 45)₂]_S stacking sequence, the effective stiffness is

Ee=2E11+5E227(45)

Because of the existence of 90° and 45° plies, the strain to failure decreases with increasing void content and the tensile strength can be calculated accordingly. It is found that the general trend of the tensile strength decreases with increasing void contents. With void contents increasing from 0.33% to 1.50%, the tensile strength of the non-aged, aged, and dried specimens decrease by 2.36%, 4.87% and 2.16%, respectively. The calculated relative tensile strength and the experimental results are shown in Fig. 13. It is seen there is little change in the normalised tensile strength when the net void content is less than 1%, and then the strength decreases with increasing void content. Because the change in the strength is not significant, it is difficult to see the critical void content around 1%. Based on the existing data, it is seen the model presented in this paper can predict the strength with satisfactory accuracy.

Fig. 13.

	Figure Option ViewDownloadNew Window
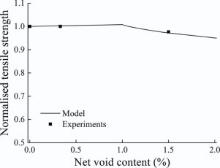	Fig. 13. Tensile strengths from model and experiments.

Because the ILSS is a matrix-dominated property, Eq. (43) is used for finding the ILSS when voids are present. The composites were made of around 60% carbon fibres. The calculated relative ILSS and various experimental data from literature^{[9, 13, 16, 18]} are shown in Fig. 14. It is seen from Fig. 14 that the model being developed in this study shows excellent agreement with the experimental data, which could be used as a useful guideline in composites design.

Fig. 14.

	Figure Option ViewDownloadNew Window
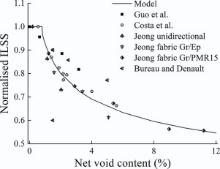	Fig. 14. ILSS from model and experiments.