In this case, the conjugate heat transfer consists of three physical aspects: flow and heat transfer in external flow field, internal cooling passages, and conduction within blade structure. During the conjugate procedure, the calculation of external and internal heat transfer is implemented together with blade conduction simultaneously. Based on the above simulations, the temperature distribution of a blade can be obtained. At the fluid-solid interface, the continuous boundary conditions of temperature and heat flux are specified by:

T_f=T_s (1)

kf∂Tf∂n=ks∂Tf∂n(2)

where T_f and Ts are the temperatures of fluid and solid domain at the interface, respectively. k_f and k_s are the thermal conductivity coefficients of fluid and solid domain, and n is the normal direction of the interface. To enforce the continuity of temperature and heat flux, during the numerical procedure, the wall temperature calculated from solid domain is defined as the temperature boundary of fluid domain, and inversely, the heat flux calculated from fluid domain is defined as the heat flux boundary condition of solid domain.

In the present study, the external flow field and temperature field of solid domain are governed by compressible turbulent flow Navier-Stokes equations and solid thermal-conductivity equations, respectively. It is worth noting that the interaction between internal cooling gas and metal substrate of the blade are defined by surface film condition with sink temperature and convection heat transfer coefficient, which is not realized by directly solving inner flow field. To improve the simulation accuracy, a conjugate heat transfer procedure is carried out by using the software ABAQUS and FLUENT, which are used to simulate solid and fluid domains, respectively.

Due to the mismatch of thermal expansion coefficient between different layers, thermal stress is generated in a turbine blade in high temperature environment. A decoupled method is adopted to calculate the stress field, in which the temperature distribution determines stress field and the influence of stress field on temperature distribution is ignored. During the elastic stage, the stress field of solid domain is governed by equilibrium equation, that is:

σ _{ij, i}+F_i=0 (i, j=1, 2) (3)

where σ _ij is the stress component, Fi is the body force. It is worth noting that the body force is not taken into account in this case (F_i = 0). Thus, we rewrite the form of Eq. (3) as

σ _{ij, i}=0 (i, j=1, 2) (4)

and the elastic stress-displacement relationship is given by:

σij=2G12ui, j+uj, i-α∆Tδij+λ̅uk, kδij(i, j, k=1, 2)(5)

where u_i is the displacement component, α is the thermal expansion coefficient, G is the shear module, λ̅is the lame constant and the term, and α Δ T, is the thermal strain.

As the plastic behavior occurs, the von Mises plasticity flow criterion is adopted to obtain plastic strain increments, which is given by:

f=J2σij-12σy2(6)

where σ _y is the yield stress. Based on the above plastic potential function, the flow rule is given by

dεijP=dλ∂f∂σijdλSij(7)

where εijPand Sijare the components of plastic strain and stress deviator, respectively. dλ is a variable relating to the plastic strain rate.

Based on the conjugate heat transfer analysis, the temperature field is obtained by using the software ABAQUS and FLUENT, which is defined as a predefined variable in ABAQUS to simulate the thermal stress field.

3.1.1. Geometric description

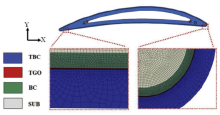
In the solid domain, a two-dimensional turbine blade with TBCs comprising four layers (TC, TGO, BC and Ni-based alloy substrate) is shown in Fig. 1. The thicknesses of TC, BC and substrate are 250 µ m, 100 µ m and 1.4 mm, respectively. Due to high temperature oxidation, TGO formed between TC and BC, whose maximum thickness can reach 10-20 µ m^[44]. And the morphological instability of TGO is a fundamental source of failure in TBCs^{[37, 45]}; however, it is experimentally verified that the TGO thickness has a negligible influence on stress in a thick ceramic coating (> 50 µ m)^[46]. In this work, the TGO morphology is not taken into account. Instead, the flat interface is assumed and the TGO thickness is set to be 10 µ m. The geometric shapes and dimensions of TC, TGO, BC, and substrate were built up in ABAQUS and then merged together with preservation of interfaces between each layer. It is worth noting that the following assumptions were introduced: (1) each layer in TBCs was perfectly bonded without defect and crack; (2) only one cooling passage was considered; (3) the effects of porosity, creep, phase transformation, sintering of TBC and TGO growth were not taken into account; (4) the thermal convection or radiation was not considered and (5) the plane-strain assumption was adopted in the thermal-stress calculation.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Illustration of the finite element model of a two-dimensional turbine blade with TBCs.

3.1.2. Material property

In the model mentioned above, each layer of a turbine blade with TBCs is considered as an isotropic and homogeneous material, and these material properties are listed in Table 1 and Table 2<sup>[47, 48], which are temperature-dependent. TC (8 wt% Y₂O₃-ZrO₂ or 8YSZ) is modeled as an elastic body, whereas the BC (NiCrAlY)、TGO (α -Al₂O₃) and substrate (GH3030) are regarded as elastic-perfect plastic materials. The detailed chemical composition of Ni-based alloy substrate (GH3030) is given in Table 3. It is worth noting that, to limit stress to the experimental level^{[46, 49]}, TGO is allowed to undergo the stress relaxation at high temperature, which is realized by introducing the yield strength of TGO at the peak temperature^[48]. At a lower temperature, TGO is like an elastic medium^[48]. As listed in Table 2, the yield strength of TGO linearly decreases from 10 to 1 GPa with the increase of temperature from 800 to 1100 ° C. The effect of creep is important when the system is subjected to thermal loading cycles at high temperature^{[50, 51]}. However, the effect of creep can be neglected here since it does not play any role in the stress redistribution due to one thermal loading cycle.

Table 1.

Table 1.

Table 1. Temperature-dependent material parameters for different layers Substrate BC TGO TC Temperature range(° C) 20-1100 20-1100 20-1100 20-1100 Young's modulus (GPa) 220-120 200-110 400-320 48-22 Poisson'sratio 0.31-0.35 0.30-0.33 0.23-0.25 0.10-0.12 Thermal expansion coefficient (10-6/° C) 14.8-18.0 13.6-17.6 8.0-9.6 9.0-12.2 Thermal conductivity(W/(cm K)) 0.88-0.69 0.058-0.170 0.10-0.04 0.020-0.017 Density(kg/m3) 8500 7380 3984 3610 Specific heat(J/(kg K)) 440 450 755 505

Table 1. Temperature-dependent material parameters for different layers

3.1.3. Meshing and elements

In the conjugate heat transfer analysis, the 4-node linear heat transfer quadrilateral element (DC2D4) is adopted to mesh the model, while a 4-node bilinear plane strain quadrilateral element (CPE4R) is adopted to mesh this model in the thermal-stress calculation. It is worth noting that the huge thickness difference between each layer makes it difficult to generate smooth mesh. Thus, finer meshes are used around the TGO zone to decrease the aspect ratio (less than 3:1) of elements, which is used to improve the accuracy of simulation results (the inset in Fig. 1). A uniform mesh is used for TGO zone with 6 elements across the TGO thickness direction. With the purpose of guaranteeing a balance between efficiency and accuracy, the number of elements is limited to an acceptable value. In this case, the element number is 285, 756 during both conjugate heat transfer and thermal-stress analysis procedure, which meets the demand of mesh sensitivity.

3.1.4. Boundary conditions

The thermal boundary conditions at the outside surface of this blade are defined by temperature and heat flux calculated from fluid domain, while the interaction between internal cooling gas and metal substrate of this blade is described by surface film condition with convection heat transfer coefficient at 300 W/(m²° C) and sink temperature at 600 ° C. During the decoupled thermal-stress analysis, the mechanical boundary conditions are imposed on point A and point B located at the inner surface (Fig. 1): (1) point A is fixed, which cannot move along the x and y directions; and (2) the displacement in x direction of point B is free, but the displacement in y direction is constrained. Thus, the turbine blade can freely expand at high temperature environment without translation and rotation.

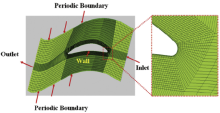
The two-dimensional external flow field model is shown in Fig. 2. The mesh generation in the fluid domain is realized by using the ANSYS software. To reduce the grid skewness and facilitate solving the boundary layer around the blade, O-grid type is utilized to mesh the whole external flow field. There are twenty two points in the fluid boundary layers, and the first point from the solid wall is located at the place where the dimensionless wall distance y + is less than or equal to unity for correct resolution of the viscous sub-layer. And the mesh is stretched away from the viscous wall using a stretching ratio between 0.8 and 2. The study on the mesh sensitivity reveals that an adequate accuracy can be achieved by using about 14, 123 elements of the fluid domain.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Computational grid of external flow field of CFD model.

Table 2.

Table 2.

Table 2. Variations of yield strength with temperature for different layers Temperature(° C) Substrate(MPa) BC(MPa) TGO(MPa) 20 800 426 10000 200 800 412 10000 400 800 396 10000 600 800 362 10000 800 800 284 10000 1000 800 202 1000 1100 800 114 1000

Table 2. Variations of yield strength with temperature for different layers

Table 3.

Table 3.

Table 3. Detailed chemical composition of Ni-based alloy substrate (GH3030) Ni Cr Fe Si Ti Al C Mn P S 73-7 19-2 ≤ 1. ≤ 0. 0.15-0.3 ≤ 1. ≤ 0.1 ≤ 0. ≤ 0.0 ≤ 0.0 6 2 5 8 5 5 2 7 3 2

Table 3. Detailed chemical composition of Ni-based alloy substrate (GH3030)

In the fluid domain, the speed and temperature fields of external gas are obtained by solving the time-average Navier-Stokes equations, where the k-ε turbulence model with non-equilibrium wall function is used. The ideal gas assumption is used to model the exhaust gas. The fluid domain involves four different types of boundary conditions: the inlet boundary, the outlet boundary, the solid wall boundary and the periodic boundary. The total temperature (T_{t, inlet}), total pressure (P_{t, inlet}) and static pressure (Ps, inlet) are fixed at the inlet boundary, while an average static-pressure (P_{s, outlet}) is imposed at the outlet boundary. At the solid wall, a no-slip boundary condition is specified for velocity. For the periodic boundaries, the fluid-domain variables are duplicated for the periodic cell pairs or vertex pairs. The detailed parameters of boundary conditions for fluid domain are presented in Table 4.

Table 4.

Table 4.

Table 4. Detailed parameters of boundary conditions for fluid domain Pt, inlet(MPa) Ps, inlet(MPa) Tt, inlet(° C) Ps, outlet(MPa) 1.422 1.4 1080 0.7

Table 4. Detailed parameters of boundary conditions for fluid domain

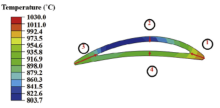
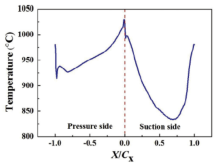
The contour plot of temperature distribution of the whole turbine blade with TBCs at the steady stage is shown in Fig. 3. And Fig. 4 shows the temperature distribution along the external surface of TC. X is the coordinate along the TBCs surface and C_x is the axial chord length. The non-dimensional lengths X/C_x with the values of 0 and ± 1 are the locations of leading and trailing edges, respectively. The locations of the suction and the pressure sides are 0.45 < X/C_x < 0.55 and -0.58 < X/C_x < -0.42. It is found that the temperatures at leading and trailing edge regions are higher than those at other regions, relatively. The maximum temperature with a value of 1030 ° C occurs at the leading edge. The trend of temperature distribution along the outside surface looks like “ valleys” , which is in good agreement with the available experimental data and numerical simulation results in literature (Fig. 5) ^{[28, 31, 32, 34]}. Furthermore, the temperature at the pressure side (-0.58 < X/C_x < -0.42) is slightly higher than that at the suction side (0.45 < X/C_x < 0.55). This may be attributed to the fact that the cooling area of the suction side is relatively larger than that of the pressure side.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Contour plot of temperature of the turbine blade at the steady stage. The regions 1, 2, 3 and 4 are the typical locations, which are the leading edge, the suction side, the trailing edge and the pressure side, respectively.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Temperature distribution on the external surface of the turbine blade with TBCs.

Fig. 5.

	Figure Option ViewDownloadNew Window
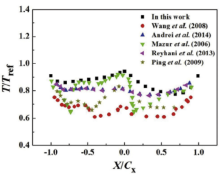	Fig. 5. Comparison of the non-dimensional temperature distribution on the external surface of TBCs with that of literature.

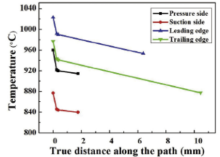
To show the difference of a temperature field in TBCs, temperature distribution along the paths (marked by red arrow in Fig. 3) in four typical regions, including the leading edge, the pressure side, the trailing edge and the suction side, is shown in Fig. 6. It appears that temperature distribution in the coating along thickness direction varies in different regions, ranging from 54 to 108 ° C. The magnitudes of temperature at the trailing edge regions are relatively higher than those of the other areas. This is consistent with the available results obtained by Ottens^[52].

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Temperature distribution along the external surface of TBCs to the substrate at the four typical locations.

It is a fact that the aircraft engines in service generally experience four stages: initial stage, heating up stage, steady stage and cooling stage. The stress levels that resulted from thermal loading at different stages are different. As we all know, the stress state in TGO has an intimate connection with the crack initiation. Therefore, the stress evolution of TGO at each stage is important for predicting the dangerous regions. Due to the independence of the chosen coordinate system, the von Mises stress is widely adopted to characterize the general stress state. Furthermore, it can accurately reflect the stress level in a turbine blade. Fig. 7(a) presents the von Mises stress contour plot of the entire blade at the end of cooling. It is shown that the stress level in TGO is dramatically higher than that in other layers. Fig. 7(b) detailedly reveals the stress evolution in TGO at different stages. The value of von Mises stress in TGO increases with the rise of temperature during the heating up stage, whereas the magnitude of stress in the vicinity of trailing and leading edges abruptly decreases as the thermal loading comes to a steady stage. This phenomenon is attributed to stress relaxation due to the higher temperature at these regions. During the cooling stage, the stress in TGO decreases as the temperature reduces. It is worth noting that the residual stress value in the vicinity of trailing and leading edges has an abrupt increase at the end of cooling, which is attributed to the non-elastic strain at these regions. This phenomenon also can be explained by the distribution of normalized equivalent plastic strain (PEEQ) in TGO presented in Fig. 8. It is found that the value of PEEQ in the vicinity of trailing and leading edge is not zero. Moreover, the magnitude of PEEQ in TGO at the leading edge is larger than that at the trailing edge. The result is similar to the temperature distribution of the outside surface shown in Fig. 4. The reason is that non-uniform temperature distribution of the turbine blade has directly impact on thermal stress field.

Fig. 7.

	Figure Option ViewDownloadNew Window
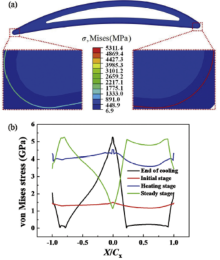	Fig. 7. von Mises stress contour plot of the turbine blade at the end of cooling (a) and stress evolution in TGO at the different stages of thermal loading (b).

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. Distribution of normalized PEEQ in TGO.

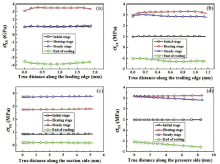
The stress evolution along X direction of the local coordinate system σ xxσ xx in TGO with the thermal loading history at the leading edge is shown in Fig. 9(a). The magnitude of stress keeps increasing during the heating up stage until this blade turns into steady state. Due to the stress relaxation, the magnitude of stress reduces to 1 GPa in the steady stage. As the thermal loading changes from steady into cooling stages, the stress σ _xx declines with the decrease of temperature, varying from tension to compression. The stress inversion process can be reasonably explained by the thermal cycling, i.e., heating expansion and cooling contraction. At the end of cooling stage, the value of residual stress at the leading edge reaches -3.5 GPa, which is consistent with the experimental data ^{[53, 54]}. Lee et al.^[53] have systematically investigated the residual stress in TGO, which is in the range of -2.0 to -4.5 GPa. Such a huge compressive stress causes the interfacial instability, which may trigger a crack in TGO. As shown in Fig. 9(b), the evolution of stress at the trailing edge has a trend similar to that of the leading edge. Compared with the stress state during the heating up stage, both the stress levels drop in the steady stage. And the value of the stress at the trailing edge is larger than that at the leading edge. However, the magnitude of residual stress at the trailing edge is less than that at the leading edge at the end of the cooling stage. The stress evolution in the middle of the suction and the pressure sides is displayed in Fig. 9(c) and (d). The variation of stress in TGO at different thermal loading stages is almost the same as that of leading and trailing edges but their values are different. It is worth noting that as the thermal loading changes from heating up into steady stages, the magnitude of stress in the middle of the pressure side slightly decreases, while the opposite phenomenon occurs in the middle of the suction side and the value of stress increases from 2.75 to 3.75 GPa. This difference is attributed to the fact that the temperature at the pressure side is relatively higher than that at the suction side during the steady stage. According to the stress evolution with thermal loading at four typical positions, it is found that the maximum tensile stress with a value of 3.75 GPa occurs in the middle of the suction side during the steady stage, which may lead to the initiation of cracks in a turbine blade when the aircraft engine is in steady flight. The maximum residual compressive stress with a value of -3.5 GPa occurs at the leading edge at the end of cooling, which may lead to crack initiation and propagation due to interfacial instability, eventually causes the coating spallation.

Fig. 9.

	Figure Option ViewDownloadNew Window
	Fig. 9. Stress evolution along X direction of the local coordinate system in TGO with the thermal loading history at the four typical locations: (a) leading edge; (b) trailing edge; (c) suction side and (d) pressure side. In the local coordinate system, X and Y directions are parallel and perpendicular to the interface of TBCs, respectively.

It should be noted that there are some limitations in this model comparing to real turbine blades under the working condition: (1) the centrifugal forces of the blades as well as forces caused by springy vibrations of the blades are not considered; (2) the effects of cooling film holes are not included; and (3) the damage of TBC, such as cracking of the TBC, is not taken into account. Due to the above limitations, the magnitude of temperature and thermal-stress fields is more or less different from that of real turbine blades under the working condition. Therefore, these will be important topics in modeling a three-dimensional turbine blade with TBCs in a future study.