Cite this Article
S. Tang, L.K. Ning, T.Z. Xin, Z. Zheng. Coarsening Behavior of Gamma Prime Precipitates in a Nickel Based Single Crystal Superalloy. Journal of Materials Science & Technology, 2016, 32(2): 172-176  
Permissions
Copyright reserved, Editorial board of Journal of Materials Science & Technology
Coarsening Behavior of Gamma Prime Precipitates in a Nickel Based Single Crystal Superalloy
S. Tang1,2, L.K. Ning1,2, T.Z. Xin1,2, Z. Zheng2
1 University of Chinese Academy of Sciences, Beijing 100049, China
2 Superalloy Division, Institute of Metal Research, Chinese Academy of Sciences, Shenyang 110016, China
Corresponding author. Tel.: +86 23970735; Fax: +86 23971927. E-mail address:lkning@imr.ac.cn (L.K. Ning).; Tel.: +86 23971729; Fax: +86 23971927 E-mail address:tzxin13s@imr.ac.cn (T.Z. Xin)..
Abstract

The γ/γ' microstructural evolution in a nickel based single crystal superalloy during load-free thermal exposure at 900 °C has been further investigated in this paper. The growth characteristics of γ′ precipitates were discussed in detail. The generation of interfacial dislocations would accelerate the rate of coalescence in the dendrite arms. The average sizes of precipitates were used to compare interface with diffusion controlled growth mechanism and no mechanism seems obviously dominant, although the square rate law gives slightly better fit. The coarsening behavior may be controlled by diffusion through the ragged interface between the γ′ precipitate and the γ matrix.

Keyword: Single crystal superalloy; Coarsening; Interfacial dislocations; Rate controlling mechanism
1. Introduction

Nickel based single crystal superalloys used as turbine blades of aeronautic gas turbines are strengthened by regularly arranged Ni3Al-typed γ ′ precipitates[1]. During high temperature service, the γ /γ ′ microstructure of nickel based superalloys gradually degrades, which has a great impact on the mechanical properties. Therefore, microstructural stability is of direct significance to the mechanical properties and coarsening behavior of γ ′ precipitates can be a concern for single crystal superalloys.

During load-free thermal exposure, the γ ′ particles would coarsen with increasing exposure time. As γ ′ particles precipitate coherently from γ matrix, the growth behavior of the particles is governed by both the interfacial and the elastic energies, which differs from classical Ostwald ripening describing a process on larger precipitates coarsening at the expense of smaller particles to lower the interfacial energy[2, 3]. The thermodynamic driving forces for coarsening are the reduction in interface area at the γ /γ ′ interface, a reduction in the γ /γ ′ lattice mismatch strain, and a reduction in the modulus misfit[4]. During thermal aging, the increase in the size of γ ′ precipitates would evolve in two ways: enlargement of its scale by Ostwald ripening if its pattern is already regular; cluster formation of γ ′ precipitates rafts parallel to the three equivalent cube axes[5]. The coarsening process may be controlled by two mechanisms[6], [7, 8]: (i) the mechanism controlled by solute diffusion through the matrix, which is described by the cube rate law:

rave3∝ K1t(1)

where rave is the average particle radius at time t and K1 is the diffusion controlled coarsening constant and (ii) the mechanism controlled by solute absorption at the γ /γ ′ interface, which is described by the square rate law:

rave2∝ K2t(2)

where rave is again the average particle radius at time t and K2 is the interface controlled coarsening constant.

Ardell and Ozolins[9] proposed a new model of coarsening, involving the diffusive mass transportation through the coherent interface between ordered γ ′ and disordered γ phases. The model demonstrated that the coarsening behavior may be controlled by diffusion through the ragged interface between the two phases. As chemical diffusion is assumed to be much faster in the γ phase than that in the γ ′ phase, the interface region lies in the periphery within the γ ′ precipitate. One major consequence of this model is that it can predict the coarsening kinetics completely independent on the volume fraction of precipitates.

Previous work had reported the coarsening behavior both in the dendrite arms (DAs) and the interdendritic regions (IRs) in a single crystal superalloy and evident coalescence phenomenon had been observed[10]. But the coarsening and coalescence mechanisms have not been interpreted and also the grow-control mechanism is unclear. The present study concentrated on the growth characteristics and accelerated coalescence phenomenon. Moreover, comparison of the rate controlling mechanism is conducted in the DAs and the IRs.

2. Experimental

The experimental material used in this study was a nickel based single crystal superalloy. The nominal chemical composition ranges of this alloy were as follows: Co, 7-11; Cr, 8-16; W, 3-6; Mo, 0-4; Re, 1-3; Al, 4-7; Ti, 0-3; Ta, 3-6 and Ni as balance (in wt%). The as-cast specimens were homogenized for 2 h at 1280 ° C and for 2 h at 1300 ° C, then air cooled to eliminate all the γ /γ ′ eutectic and coarse γ ′ particles. Afterwards they were aged according to the following system: heating at 1120 ° C for 4 h followed by air cooling, then heating at 900 ° C for 24 h followed by air cooling. Load-free thermal exposure experiment was performed at 900 ° C for periods of 100-500 h in a box furnace. Microstructure observation was made at the end of the experiments. The specimens were mechanically polished and etched with an agent of 5 g CuSO4 + 20 mL HCl + 20 mL H2O for 40-50 s to deeply dissolve the γ ′ . The INSPECT F50 field-emission scanning electron microscope (SEM) was used for microstructure analysis. The Image-Pro Plus and Origin software were applied to analyze the resulting micrographs and data, respectively[10].

3. Results and Discussion
3.1. Growth of γ ′ particles

In the course of thermal exposure, the γ ′ particles both in the DAs and the IRs would grow through the Ostwald ripening process and the shape of the particles kept square or rectangular by virtue of elastic stresses. Apart from this coarsening mechanism, a large number of γ ′ particles grew by coalescence in the DAs while coalescence only occurred in very limited IRs[10]. According to Thornton et al.[3], that the particles become evidently spatially correlated in the DAs can be attributed to the different concentrations in the γ matrix at the γ /γ ′ interface. Because in the DAs particle sizes of heat-treated state are inhomogeneous and many particles present obvious rectangular rather than square shape[10], and the interfacial concentrations would vary in the light of particles with different sizes and shapes. On the one hand, the larger particles may easily grow at the expense of smaller particles with higher concentrations. On the other hand, elongated shape of γ ′ particles would have various concentrations along the interfaces. The mass flow is from the interfaces with higher concentrations to the ones with lower concentrations for every single particle, leading to γ ′ dissolution of higher-concentration interfaces and γ ′ precipitation of higher-concentration interfaces. Thus particles would move and be in alignment with particles nearby. Finally, diffusion-induced coalescence occurs among particles.

3.2. Acceleration of γ ′ coalescence

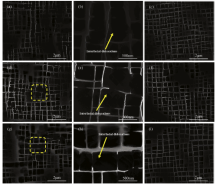
As apparent coalescence took place in the DAs[10], the γ ′ plates make it hard to keep the interface coherency between γ ′ precipitates and γ matrix. Interfacial dislocations may be induced to release the coherency stresses. According to the method proposed by Epishin et al.[11, 12], interfacial dislocations could be observed as a result of the pressure of them against the precipitate-matrix interface and they are visualized by deep selective etching. Through similar deep selective etching technique in our experimental alloys, interfacial dislocations can be observed by SEM in the DAs and interfacial dislocations can barely be found in the IRs after a thorough observation of all thermal-exposure specimens (Fig.1). Fig.1(a, d, and g) exhibits the typical γ /γ ′ microstructure of specimens exposed for 100 h, 300 h and 500 h in the DAs, respectively. Interfacial dislocations can be detected in the segments marked by yellow dotted rectangular frame and these segments with higher magnification are shown in Fig.1(b, e, and h). Interfacial dislocations, as a short-circuit diffusion path, can speed up the γ ′ coalescence. In order to account for the relationship between dislocations and coalescence of γ ′ particles, the atom radius and mobility of alloying elements are considered and plotted in Fig.2[13, 14], and a schematic illustration is presented in Fig.3 as well. When interfacial dislocations are produced on highly stressed particle faces during thermal exposure, atoms with small radius would segregate toward these defects to decrease the total energy of the alloy. Simultaneously taking the atom mobility of alloying elements into consideration, partial Cr and Co atoms in the γ matrix rather than that in the γ ′ precipitates would diffuse toward interfacial dislocations since diffusion in the γ ′ is generally slower than that in the γ [15, 16]. Cr and Co atoms are then capable of diffusing from γ matrix corridors devoid of dislocations toward that filled with dislocations due to the chemical gradient. The flux is accompanied by a crossed flux of atoms with high mobility (Al, Ti, Ta) (see Fig.2). Such cross diffusion leads to the preferential growth and ultimately gives rise to the coalescence of γ ′ precipitates. The diffusion trend has also been verified through EDS Line scanning of the dendrite-arm γ matrix in the experimental alloy exposed for 500 h as an example (Fig.4). It can be found that the area with dislocations (A) has higher Ta, Al concentration and lower Cr, Co concentration compared to that without dislocations (B). Thus cross diffusion would happen and the theoretical analysis are proved.

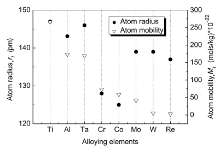Fig.1 Typical γ /γ ′ microstructure of specimens exposed for 100 h (a), 300 h (d) and 500 h (g) in the DAs is displayed and higher magnification of the yellow dotted rectangular frames is shown in (b), (e) and (h). Interfacial dislocations can be detected marked by yellow arrows. The γ /γ ′ microstructure of specimens exposed for 100 h (c), 300 h (f) and 500 h (i) in the IRs is also presented for comparison.

Fig.2 Comparison of atom radius and mobility of alloy elements is illustrated. For simplicity, only the atom mobility in pure nickel at 900 ° C is considered and calculated referring to the Appendix.

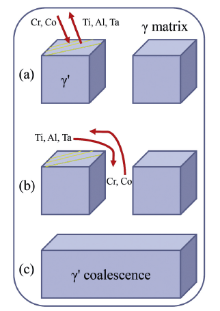Fig.3 Schematic illustration for acceleration of γ ′ coalescence due to interfacial dislocations (interfacial dislocations are yellow lines on the γ /γ ′ interface).

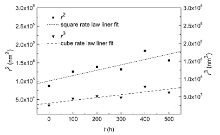
Fig.4 Line scanning of the dendrite-arm γ matrix in the experimental alloy exposed for 500 h.

3.3. Rate controlling mechanism

The coarsening kinetics both in the DAs and the IRs and comparison of the cube rate law between them had been demonstrated. The cube rate law gives a much better fit for the IRs than for the DAs[10]. However, the growth controlled mechanism for the DAs and the IRs seems unclear. The results of the average particle size for the DAs and the IRs were used to assess the rate controlling mechanism. If the growth is matrix-diffusion controlled, then it follows the cube rate law (Eq. (1)), whereas if the growth is interface controlled, the square rate law (Eq. (2)) applies. For the experimental specimens in our work, both equations were plotted and the fitting parameter R2 was listed in Table 1. An example of the graphs is shown in Fig.5 for the DAs. When comparing the fitting parameters of the two rate controlling mechanisms, it is found that the square rate law gives a slightly better fit for both regions. But none of them is clearly dominant and no definitive conclusions can be drawn from this comparison. Referring to the simulation results by Vaithyanathan et al.[17], a larger volume fraction of precipitates have smaller aspect ratio, which is the longest edge length to the shortest edge length of cuboidal precipitates. As the γ ′ volume fraction in the IRs is always larger than that in the DAs [18, 19], γ ′ precipitates in the IRs may have a lower aspect ratio. This result shows excellent qualitative agreement with our experimental observations. Based on the new coarsening model built by Ardell and Ozolins[9], coarsening is controlled by diffusion in the region of the ragged interface between the γ ′ precipitate and the γ matrix and there is no effect of volume fraction on kinetics. In accordance with the interpretation by the model, if δ Dγ > > rDI (where δ is the thickness of the interface region, which is in the interior of a γ ′ precipitate, r is the radius of the precipitate, Dγ is the chemical diffusion coefficient in the γ matrix and DI is the average chemical diffusion coefficient in the interface region δ ), the growth rate can be expressed by the square rate law. Moreover, elastic stress and aspect ratio become increasingly more important with time[2, 3] and they should be taken into consideration during the diffusion process. The kinetics difference between the two regions still needs further investigation.

Table.1 Values of the fitting parameter R2 for the diffusion and interface controlled rate laws

Fig.5 Relation between the two mechanisms of coarsening for the DAs.

4. Summary

(1)The coarsening behavior of γ ′ particles has been discussed. That the particles become evidently spatially correlated and coalesced can be attributed to the different concentrations in the γ matrix at the γ /γ ′ interface.

(2)The generation of interfacial dislocations on highly stressed particles would quicken the γ ′ coalescence process.

(3)The average sizes of precipitates are compared for both interface and diffusion controlled growth and no mechanism seems obviously dominant in both the DAs and the IRs, although the square rate law gives slightly better fit. The coarsening behavior may be controlled by diffusion through the ragged interface between the γ and γ ′ , and also the effect of elastic stress should be considered.

The mobility Mi for alloying elements in nickel [13]:

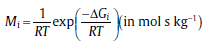
Δ GAl=284000-RTln(7.5× 10-4)

Δ GTi=269267.07+68.81T

Δ GCr=287000+64.40T

Δ GCo=277380.37+74.47T

Δ GMo=269133.21+84.35T

Δ GTa=226313+109.20T

Δ GRe=245037+127.54T

Δ GW=312426+64.39T

where R = 8.31 J K-1mol-1 is the gas constant, T is temperature in K, and Δ Gi is the diffusion activation energy in J mol-1.

Acknowledgements Acknowledgments:We thank Mr. Y.S. Yu (Dalian University of Technology) and Mr. E.Z. Liu (Institute of Metal Research) for the useful discussion.

Appendix

The authors have declared that no competing interests exist.

Reference
[1] R. C. Reed The Superalloys: Fundamentals and Applications (first ed. ) (2006) Cambridge [本文引用:1]
[2] K. Thornton, N. Akaiwa, P. W. Voorhees Acta Mater, 52(2004), pp. 1353-1364 [本文引用:2]
[3] K. Thornton, N. Akaiwa, P. W. Voorhees Acta Mater, 52(2004), pp. 1365-1378 [本文引用:3]
[4] M. V. Acharya, G. E. Fuchs Mater. Sci. Eng. A, 381(2004), pp. 143-153 [本文引用:1]
[5] F. R. N. Nabarro Metall. Mater. Trans. A, 27(1996), pp. 513-530 [本文引用:1]
[6] D. McLean Met. Sci, 18(1984), pp. 249-256 [本文引用:1]
[7] R. J. White Mater. Sci. Eng. A, 40(1979), pp. 15-20 [本文引用:1]
[8] R. J. White, S. B. Fisher Mater. Sci. Eng, 33(1978), pp. 149-157 [本文引用:1]
[9] A. J. Ardell, V. Ozolins Nat. Mater, 4(2005), pp. 309-316 [本文引用:2]
[10] S. Tang, Z. Zheng, L. K. Ning Mater. Lett, 128(2014), pp. 388-391 [本文引用:6]
[11] A. Epishin, T. Link, G. Nolze J. Microsc-Oxford, 228(2007), pp. 110-117 [本文引用:1]
[12] T. Link, A. Epishin, M. Paulisch, T. May Mater. Sci. Eng. A, 528(2011), pp. 6225-6234 [本文引用:1]
[13] A. Engstrom, L. Hoglund, J. Agren Metall. Mater. Trans. A, 25(1994), pp. 1127-1134 [本文引用:2]
[14] A. P. Miller Lange's Hand book of Chemistry (fourth ed. ) (1941) [本文引用:1]
[15] J. Y. Buffiere, M. Ignat Acta Metall. Mater, 43(1995), pp. 1791-1797 [本文引用:1]
[16] Y. Minamino, S. B. Jung, T. Yamane, K. Hirao Metall. Mater. Trans. A, 23(1992), pp. 2783-2790 [本文引用:1]
[17] V. Vaithyanathan, L. Q. Chen Acta Mater, 50(2002), pp. 4061-4073 [本文引用:1]
[18] R. C. Reed, D. C. Cox, C. M. F. Rae Mater. Sci. Technol, 23(2007), pp. 893-902 [本文引用:1]
[19] U. Hemmersmeier, M. Feller-Kniepmeier Mater. Sci. Eng. A, 248(1998), pp. 87-97 [本文引用:1]