Cite this Article
Peitao Liu, Shoulong Wang, Dianzhong Li, Yiyi Li, Xing-Qiu Chen. Fast and Huge Anisotropic Diffusion of Cu (Ag) and Its Resistance on the Sn Self-diffusivity in Solid β-Sn . Journal of Materials Science & Technology, 2016, 32(2): 121-128  
Permissions
Copyright reserved, Editorial board of Journal of Materials Science & Technology
Fast and Huge Anisotropic Diffusion of Cu (Ag) and Its Resistance on the Sn Self-diffusivity in Solid β-Sn
Peitao Liu, Shoulong Wang, Dianzhong Li, Yiyi Li, Xing-Qiu Chen
Shenyang National Laboratory for Materials Science, Institute of Metal Research, Chinese Academy of Sciences, Shenyang 110016, China
Corresponding author. Prof., Ph.D.;Tel.: +86 439 23971560. (X.-Q. Chen). E-mail address:xingqiu.chen@imr.ac.cn (X.-Q. Chen).
Abstract

The site preferences, fast and huge anisotropic diffusion mechanisms of Cu (Ag) in β-Sn as well as their reduction on the self-diffusivity of Sn, have been investigated using the first-principles and ab initio molecular dynamics methods. We have found that Cu prefers the interstitial site, whereas Ag is preferable in the substitutional site, which is mostly dominated by their different size factors. Electronic structure further evidences that the d- s hybridization between the solute and the host atom also contributes to the site preferences. It is also deduced that the fast diffusion of Cu (Ag) is mostly due to the interstitial diffusion mechanism and their diffusivity can be correlated with the amount of their respective interstitial solution. Their faster diffusion along the c-axis can be attributed to the extremely low migration energy barrier caused by the straight tunnel of considerable size with the screw axis symmetry of 2π/4 along the c-axis. Furthermore, it is found that during the process of diffusion the interstitially dissolved Cu (Ag) atoms would combine with the nearby Sn-vacancy and further annihilate the vacancy, thereby reducing the self-diffusion of Sn.

Keyword: Diffusion; Electromigration; β-Sn; First-principles
1. Introduction

In materials science and engineering, diffusion, which is one of the fundamental processes, often occurs naturally, in particular, as temperature rises. This process easily governs the structure, processing and properties of materials and even plays an important role in determining device lifetime[1]. In fact, with the presence of defects and impurities in materials the diffusion can be more complicated, such as the carbon diffusion in iron[2]. From the viewpoint of theoretical mechanism, the diffusion should be always understood through competitive energy barriers in seeking the screening pathway in the hosting lattice space[2]. Among all metal elements, Cu is a highly unique one, which exhibits fast diffusion in many semiconductors. For instance, at 500 ° C the interstitial diffusion coefficients of Cu in Ge and Si were measured to be as high as 2.8 × 105 cm2/s and 0.76 × 105 cm2/s, respectively[3]. The similar behavior of Cu was also observed in GaAs, InSb, AlSb, InAs, BiTe, AgSe, GaAs, ZnS, and ZnSe. Recently, the mechanism of the fast diffusion of Cu in CdTe has been attributed to the so-called strong d-s coupling between Cu d levels and unoccupied host s levels. The results demonstrated that due to the absence of active d level in hosting CdTe, the strong d-s coupling makes Cu diffusion faster in many similar semiconductors [4]. Even, the experiment demonstrated that the liquid-like mobility of Cu in the rigid Se face-centered cubic semiconductor was suspected to play a crucial role in causing a high ZT thermoelectric value (1.5) of Cu2-xSe [5].

Sn-based solders have become widely used as interconnections in the integrated circuits and electronic pack system due to their low eutectic temperature, high thermal conductivity and low thermal expansion, as well as the good weldability[6]. However, the electromigration (EM) failure[7] that happens in Sn-based solder bumps greatly reduces the welding reliability and the lifetime of electronic devices[8]. To date, a large number of experimental and theoretical studies have been conducted to investigate the EM mechanism of SnPb[9, 10, 11], SnCu[12], SnAg[13, 14], SnBi[15], and SnAgCu[16]alloy solder joints. The effects of Cu are diverse during the EM process. On the one hand, it was demonstrated to become the dominant migrating species in SnCu[12] and SnAgCu[16] alloys and, on the other hand, a small addition of Cu (or Ag) in the Pb-free Sn-based solders shows a good effect to prolong the EM lifetime[16, 17]. Because the EM process is a directional mass transport process[18, 19], besides the electric field strength and temperature, it is directly diffusion-controlled. In order to better understand why Cu (Ag) is the primary migrating species and how to overcome the EM failure and prolong the Sn-based solder's lifetime, it is certainly essential to investigate the solutes diffusion process, in particular, their site preferences and diffusion mechanisms behind inβ -Sn.

Using first-principles and ab initio molecular dynamics (abMD) methods, for the first time, we have investigated site occupation and huge anisotropic diffusion mechanisms of Cu (Ag) in β -Sn as well as its resistance on the self-diffusivity of Sn, and compared with the available experimental results. For comparison purpose, Au, Zn and Cd are also investigated. The paper is organized as follows. Following the introduction, Section 2explains the computational details. Section 3 presents our calculated results and corresponding discussions. Finally we give our conclusions in Section 4.

2. Computational Details
2.1. First-principles calculations

Our calculations are based on the framework of density functional theory[20, 21] as implemented in the Vienna ab initio Simulation Package (VASP) [22, 23]. All calculations are performed using the projector augmented wave (PAW)[24] potentials and the generalized-gradient approximation (GGA), with the exchange-correlation functional of Perdew-Burke-Ernzerhof (PBE)[25]. We use a Fermi smearing of electronic occupancy with a width of 0.05 eV and plane wave cut-off energy of 480 eV, which is found to be sufficient for highly precise energetics for all the elements (Noble metals, Zn, Cd and Sn) considered in this work. The Brillouin zone is sampled by a 6 × 6 × 6 k-point mesh generated using the Monkhorst-Pack scheme [26]. In order to match the experimental dilute concentration of solutes in the Sn-based solders, here 64-lattice supercell (2 × 2 × 4 bct β -Sn unit cell) is constructed to calculate the interstitial solution energy, substitutional solution energy, and vacancy formation energy as well as the migration energy. Note that the point defects here are formed by inserting a new impurity atom, or substituting (subtracting) one host atom. All DFT calculations are fully relaxed at constant volume using the quasi-Newton algorithm to find the possible minimum energy, with the energy difference less than 1 × 10-6 eV and the force acted on per atom less than 0.02 eV/Å . With these DFT parameters, the calculated lattice constants of β -Sn are a = 5.919 Å and c = 3.230 Å , which are slightly larger than the experimental results, 5.831 Å and 3.166 Å due to the GGA approximation. The climbing-image nudged elastic band (CI-NEB) [27] method is employed to calculate the migration energy barriers of the solute diffusion in the β -Sn. In the present work, all the images are kept separated using a spring force constant of 5 eV/Å and then are relaxed using conjugate gradient algorithm until the maximum force acting on an atom is less than 0.05 eV/Å .

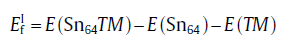For the interstitial diffusion mechanism, the activation energy ( Qtot1) is made up of two terms. The first term is the interstitial solution enthalpy ( Ef1), and the second one is the migration energy barrier ( Emig1). Ef1can be calculated as:

(1)

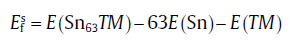where E(Sn64) is the energy of 64-atom defect-free supercell, E(Sn64TM) the energy of supercell with one TM atom occupying the interstitial site, and E(TM) the reference energy of single TM atom within the energetically stable bulk state. While for the vacancy-mediated diffusion mechanism, the activation energy Qtots() consists of three parts: substitutional solution energy ( Efs), vacancy formation energy in the presence ofTM in Sn63TM supercell ( EfVac) and migration energy of vacancy ( EmigVac). Efscan be expressed as:

(2)

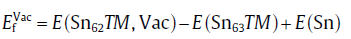where E(Sn63TM) is the energy of supercell Sn63TM with one TM atom substituting the Sn lattice. Vacancy formation energy ( EfVac) in the presence of TM nearby in the supercell Sn63TM can be calculated as follows:

(3)

where E(Sn62TM, Vac) is the energy of supercell with one substitutional atom TM and one nearby Sn vacancy. Obviously, the sum of Efsand EfVaccan also be regarded as the formation energy of the substitutional solute TM-vacancy pair.

2.2. Ab initio molecular dynamics simulations

In order to investigate the effects of Cu (Ag) addition on the self-diffusivity of Sn, we have further performed ab initio molecular dynamics (abMD) simulations in a canonical ensemble within a 4 × 4 × 4 supercell. Because of the large supercell, only one Г -centeredk-point is used for Brillouin zone integration to keep the computational cost at a reasonable level. Verlet algorithm is employed for the integration of the atomic equations of motion and the time step was chosen to be 2 fs such that the integration is stable and at the same time computational effort is acceptable. At the starting point of the abMD simulations, the samples are assigned to an initial temperature of 100 K according to a Boltzmann distribution. Then, they are heated up to the desired temperature (300 and 500 K) by velocity scaling over 3 ps. After the desired temperature is achieved, the samples are kept equilibrated at the specified temperature for 5 ps at constant volume with a Nosé thermostat [28]. This step is done just to make sure that the system is in the equilibrium state. Finally, the abMD simulations for the diffusion were performed for 20 ps. Within the abMD framework, the diffusion coefficient is defined as [29]:

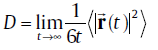(4)

where is the average mean square displacement (MSD), which is averaged over all Sn atoms. It can be obtained as:

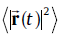
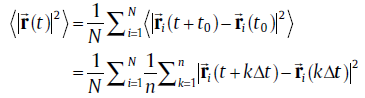(5)

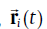
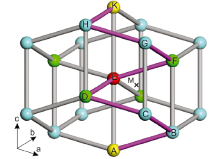
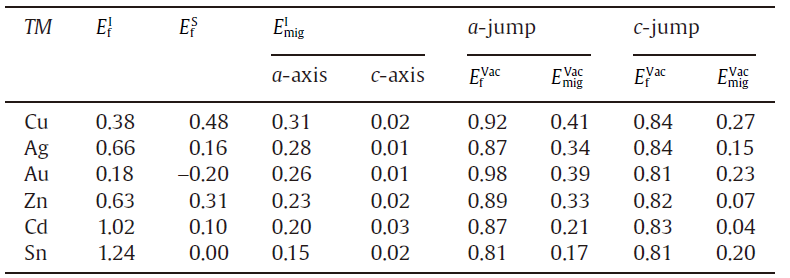
where N is the total number of Sn atoms, is the displacement of the i-th Sn atom at the time of t, n equals half of the total steps in the diffusion process of the simulations and Δ t is the simulation time step.

3. Results and Discussion
3.1. Site preferences

As illustrated in Fig.1, each Sn atom has four nearest neighbors (3.0667 Å ), directed ~15° out of the ab-plane, and two next nearest neighbors (3.241 Å ) in the c direction. The point M, the centroid of the polyhedron composed by C, D, E, and F, with screw axis symmetry of 2π /4 along the c-axis direction, is a representative interstitial site. The coordination of M is (x/4, y/4, z/8) with x, y, z all odd integers [30]. Table 1 summarizes the resulting theoretical results of their site preferences in β -Sn. It can be seen that Cu prefers to occupy the interstitial site M, whereas other metals (Ag, Au, Zn and Cd) commonly prefer to substitute the Sn site. Although Ag, Au and Zn are energetically more favorable in the substitutional site, the possibilities to dissolve interstitially cannot be ruled out since both their interstitial and substitutional solution enthalpies are relatively low in comparison with the Sn vacancy formation energy of 0.81 eV, as illustrated in Table 1. In particular, it is worth noting that the substitutional solution enthalpy of Au is negative (-0.20 eV), indicating that the solution of Au in Sn is exothermic, in accordance with the relatively large solubility of Au in tin[31]. In addition, the negative substitutional solution enthalpy of Au accounts well for the experimental observation that Au atoms dissolves mostly entirely in the substitutional positions[31]. Unexpectedly, Cu, however, is energetically favorable in the interstitial site.

Fig.1 Crystal structure of β -Sn showing an interstitial site at M, the centroid of C, D, E and F. Oblique lines join nearest neighbors; vertical lines join next nearest neighbors. The jumps from site E to the nearest-neighbor sites (green balls) are called a-jump, while the jumps from site E to the next-nearest-neighbor sites (yellow balls) are called c-jump. Note that A, B, C, D and E (purple lines) are symmetrized with a screw axis symmetry of 2π /4 along the c-axis direction.

Table.1 Computed interstitial solution energies ( Ef1), substitutional solution energies ( Efs), migration energies ( Emig1) for solute TM diffusing by the interstitial mechanism along the a-axis and c -axis, and vacancy formation energies ( EfVac) as well as vacancy migration energies ( EmigVac) for TM diffusing by the vacancy mechanism in the a-jump and c-jump. The energy unit is eV

Empirically, the interstitial solution behavior of solutes was thought to closely correlate with their atomic radii according to the Hä gg's rule[32], which claimed that the interstitial solid solutions occur only when the solute is much smaller in size than the solvent. Apparently, this is not the case here. Take Cu for instance, the size ratio between the solute's atomic diameter and solvent's rCu/rSn is equal to 0.74, neither favorable to interstitial solution (0.4-0.6) nor favorable to the substitutional solution (0.8-1.0)[32]. The interstitial solution character of noble metals has also been observed in other polyvalent metals such as lead[33, 34], germanium[35], indium[36] and erbium[37]. To understand the physical origin of the noble metal interstitial character in these polyvalent metals, Anthony and Turnbull[38] ascribed this to the d-d correlation binding between the ion cores. They claimed that the binding was present only when the noble-metal solutes were at the interstitial site, but it was absent when the noble-metal solutes dissolved substitutionally. However, this theory could not explain the fact that in polyvalent Cd metal the noble-metal solutes preferred the substitutional site and diffused by the vacancy mechanism [39]. In addition, it is experimentally concluded that the noble-metal solutes diffuse in Sn by the interstitial mechanism [40, 41]. Our calculations, however, show that Ag and Au are found to prefer the substitutional site rather than the interstitial site due to the relatively low substitutional formation energy (see Table 1).

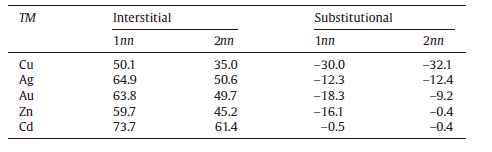
In order to uncover the reasons as to the site preferences, we first focused on the solutes' size factors. As shown in Table 2, it can be seen that all the considered solutes would generate the local lattice expansion or contraction when occupying the interstitial sites or substitutional sites, respectively. Because the atomic positions are relaxed at the fixed volume, it means that the larger the relaxation of the Sn atoms around the solutes is, the larger the strain energy they generate. For instance, in comparison with other solutes, Cu induces the smallest strain energy when occupying the interstitial site, but rather generates the largest strain energy when occupying the substitutional site due to its smallest ionic radius. In contrast, Cd induces the smallest strain energy in the substitutional site but the largest strain energy in the interstitial site. These facts are well consistent with our solution energy calculations showing that Cu prefers the interstitial sites, whereas Cd prefers the substitutional sites. Thus, it can be concluded that the site preferences of solutes in β -Sn are mostly dominated by their respective size factors.

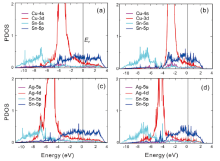
Table.2 Relaxation (%) of the first-nearest-neighbor (1nn) and second-nearest-neighbor (2nn ) Sn atoms around the solutes occupying the interstitial and substitutional site, respectively. The relaxation is defined as ∆di/di0×100% with ∆di=di-di0 where di0 and di are the TM-Sn distance before and after relaxation, respectively

In addition, the electronic structure has been analyzed in detail as illustrated in Fig.2(PDOS for the Au, Zn and Cd case are not shown here). It can be found that wherever the solutes occupy, the typical features can be observed: (i) within all cases the fully occupied Sn-5s-like states are dominant in the low-lying energy range while the Sn-5p-like states in the high energy region become partially occupied, crossing the Fermi level. (ii) Upon the different solutes, the energy locations of the d-like states introduced by interstitial or substitutable solute metals, vary highly. Basically, no matter where the solute atom occupies, the d-like states significantly shift towards the low-lying energy region from Cu to Ag to Au ( Fig.2). It should be noted that in the interstitial case the Cu 3d-like states show highly obvious electronic hybridizations with the Sn 5s-like states to form the bond between Cu 3d-like and Sn 5s-like states (called d-s coupling). However, such a d-s coupling is too negligible to be seen in the substitutional case of Cu. This d-s coupling agrees well with the interstitial solution character of Cu. In contrast, in the case of Ag the d-s coupling effect has been found to be much stronger in the substitutional site than the interstitial site (compare Fig.2(b) and (d)). For instance, for Ag occupying the substitutional sites the Ag-4d states follow almost rigidly the Sn-5s states from -8 to -6 eV due to their stronger coupling. In addition, the density of states for Sn-5s orbitals is larger and more low-lying in the case where Ag occupies the substitutional site, which makes the system more stable. The similar situations have also been observed for the other solutions of Au, Zn and Cd (not shown here). As a result, we comment that the so-called d-s coupling effect between the solute TM and the host Sn atom also contributes to determining the stable site occupation.

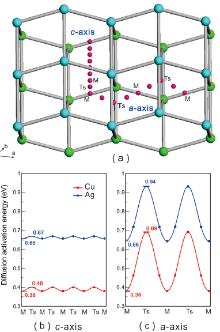
Fig.2 Projected densities of states of Cu (Ag) and its first-nearest-neighbor Sn atom for Cu (Ag) occupying the interstitial site (the two left-hand panels) and substitutional site (the two right-hand panels), respectively.

3.2. Migration behaviors and diffusion mechanisms

We have further investigated the migration behaviors of the solutes by considering two most possible mechanisms: the interstitial mechanism and the vacancy mechanism. As illustrated in Fig.3(a) for the interstitial diffusion mechanism, two kinds of diffusion pathways can be classified, namely, along the a-axis and c-axis, respectively. Similarly, for the vacancy diffusion, there are two types, a-jump and c-jump by taking into account the lattice symmetry of β -Sn. The former a-jump refers to that the solutes jump from a substitutional site to its nearest-neighbor vacancy and the c-jump means that the solutes jump from the substitutional site to its next-nearest-neighboring vacancy along the c-axis (i.e., Fig.1). Table 1 summarizes the diffusion energy barriers of four kinds of diffusion pathways for all the solutes considered here. Strikingly, within the interstitial mechanism the migration energies for any solutes along the c-axis are extremely low, with the values being nearly 0 eV within the margin of calculated error, whereas the corresponding energies along the a-axis are much larger (c.f., Table 1). For instance, the migration energies for the interstitial solutes of Cu and Ag along the c-axis are as low as 0.02 eV and 0.01 eV, respectively (see Fig.3(b)). However, their respective values are increased to 0.31 eV and 0.28 eV along the a-axis (see Fig.3(c)). Accordingly, these results demonstrate that the interstitial solutes diffuse much faster along the c-axis than in the ab-plane.

Fig.3 Panel (a) displays the diffusion pathway (the pink balls) for interstitial atom jumping along the c-axis and a-axis. The cyan and green balls represent the two different layers of β -Sn. Panels (b) and (c) shows the diffusion energy curves of Cu and Ag along the c-axis and a-axis, respectively.

Within the vacancy mechanism of diffusion, we first computed that the vacancy formation energy EfVacof Sn in pure β -Sn is 0.81 eV. When the solute TM is introduced in β -Sn, EfVacwould be affected by the presence of TM interacting with the vacancy. As evidenced in Table 1, it has been found that for the c -jump the EfVacalmost remains unchanged due to the relatively long interaction distance between vacancy and TM atom, whereas it is enhanced to some extent for the a-jump. This fact reveals that along the a-jump there is a stronger attractive interaction between the solute (TM) and the vacancy. In addition, our calculations also found that the migration energy of the solute TM for the a-jump is much larger than that for the c-jump (see Table 1). Different from the diffusion of the solutes, our calculations further uncovered that self-diffusion of Sn shows an opposite tendency. Its migration energy for the c-jump is even slightly higher than that for the a-jump, indicating that Sn diffuses relatively faster along the a-jump. This situation of the Sn self-diffusion is consistent with the experimental observations [42, 43, 44].

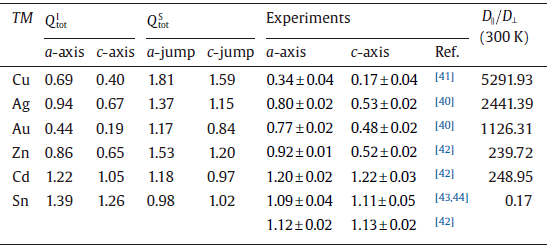
Undoubtedly, the solute diffusivity in β -Sn depends mainly on the total activation energy. As defined in Section 2.1, we further derived the total diffusion activation energies for each solute in the Table 3 and Fig.4 as compared with available experimental data. It can be seen that for both a-axis and c-axis the total activation energies of all the noble metals for the interstitial mechanism are much lower than those for the vacancy-mediated mechanism. This fact demonstrates that the solutes Cu, Ag and Au prefer to diffuse through the interstitial mechanism. As a further support, our derived interstitial diffusion activation energies are in reasonable agreement with available experimental data[40, 41] (see Table 3). It needs to be emphasized that the interstitial diffusion of the noble metals were also observed in other polyvalent metals[33, 34, 35, 36, 37] and many semi-conductors[4, 45], which accounts for their fast diffusion. From Table 3, the solute of Zn also exhibits quite similar characteristic with the noble metals, in accordance with the experimentally observed fast diffusion of Zn in β -Sn [42, 43, 44, 45, 46]. In contrast, the self-diffusion of Sn is mainly vacancy-mediated since its activation energy by the vacancy mechanism is relatively smaller and much closer to the experimentally obtained data [42, 43, 44]. In addition, the obvious activation volume (5.3 ± 0.3 cm3 g atom-1) of the self-diffusion of Sn measured by Coston and Nachtrieb[43] evidenced that Sn atoms indeed diffused by the vacancy mechanism. However, the solute of Cd is highly unique because it diffuses either by interstitial mechanism or by vacancy mechanism. The activation energies for both diffusion mechanisms are very close to each other. No matter which mechanism Cd adopts to diffuse, its activation energy is the largest among all the solutes considered here. This fact is the reason as to why Cd diffuses the most slowly in β -Sn [42].

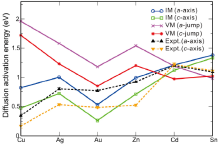Table.3 Computed and experimental total diffusion activation energies (eV) for TM diffusing along the a-axis and c -axis by the interstitial mechanism ( Qtot1) and vacancy mechanism ( Qtots), respectively. The diffusion anisotropy ratio D∥/D⊥ at 300 K is also displayed

Fig.4 Calculated and experimental diffusion activation energies (eV) for solute TM diffusing along the a-axis and c-axis by the interstitial mechanism (IM) and vacancy mechanism (VM), respectively.

In comparison with available experimental data in Fig.4, besides a good agreement in their trends, the magnitude of calculated total activation energies for different solutes exhibits some discrepancies. For instance, the total diffusion activation energies of the interstitially dissolved Cu atoms are derived to be 0.40 eV and 0.69 eV along the c-axis and a-axis, respectively, being much larger than their corresponding experimental data of 0.17 eV and 0.34 eV [41]. Hence, it needs to be mentioned that several possible reasons may cause their discrepancies. First, according to our above analysis of site preferences, the noble-metal elements Cu, Ag and Au and the element of Zn could possibly dissolve, both interstitially and substitutionally. As a result, in the real measurements both of these two diffusion mechanisms could exist, which was experimentally evidenced by Ascoli and Poletti's work[47]. Second, the experimentally measured results would inevitably be affected by the specific complicated experimental factors, such as temperature, pressure, concentration, and defects, and so on. Third, it is found that the solute's diffusivity could be correlated with the amount of the interstitial solution. For instance, although the interstitially dissolved Au atom has a much smaller activation energy compared with that of Cu (see Table 3), it diffuses more slowly than Cu[31]. This fact is primarily likely due to the fact that a rather small proportion of dissolved Au atoms (about 5% or less) occupy the interstitial sites[31]. In contrast, the proportion of the interstitially dissolved Cu atoms in β -Sn is much higher because of its lower interstitial solution enthalpy. In addition, given the fact that the equilibrium interstitial solubility of Cd and Sn themselves are extremely low (less than 10-9 at 500 K), their diffusion are thus expected to be significantly slow.

3.3. Anisotropy of diffusions

According to the Le Claire's theory[48], where K is a geometrical factor depending on the crystal structure and the diffusion mechanism, ν is the vibration frequency of the diffusing atom, δ is the jump distance, Δ S is an entropy change associated with the diffusion, Q is the diffusion activation energy, KB is the Boltzmann constant and T is the temperature. For the interstitial mechanism of diffusivity, the parameters of K, ν , and Δ S can be assumed to be same along the a-axis and c-axis. 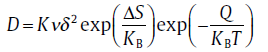The diffusion activation energy Q is equal to the sum of Ef1and Emig1. Therefore, within the interstitial mechanism the anisotropic ratio (D||/D⊥) of the directional diffusions between D|| along the c-axis and D⊥ along the a-axis can be estimated as follows:

(6)

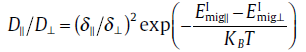(7)

where the jump distances are δ ∥≈ 0.8 Å , along the c -axis and δ ⊥≈ 3.0 Å , along thea -axis, and Emih||1and Emih⊥1are the migration energies of the solute TM along the c-axis and a-axis, respectively.

Within the vacancy mechanism, based on Eq. (6) the anisotropic ratio, D||/D⊥ can be obtained by:

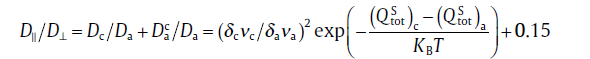(8)

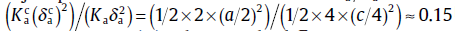
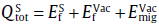
where Dc and Da are the diffusion coefficients for the c-jump and a -jump, respectively. The term of is the correction term of the anisotropic ratio because our defined a-jump is not strictly perpendicular to the c -axis.represents the c-axis component of the a -jump diffusion and their ratio of can be derived as [43]. In addition, in Eq. (8)the total diffusion activation energies . Within the vacancy-mediated diffusion, for the c -jump δ ∥=3.24 Å , and for the a -jump δ ∥=3.07 Å . We need to particularly note that the vibration frequency ν for the c-jump is different from that for the a-jump. Based on the work of Coston and Nachtrieb [43], ν ∥/ν ⊥≈ 0.257.

Importantly, our above analysis has already revealed that Cu, Ag, Au and Zn prefer to the interstitial diffusions but Cd and Sn itself like to diffuse through the vacancy-mediated mechanism. For the solutes Cu, Ag, Au and Zn, their anisotropic ratio of the diffusion can be derived by Eq. (7), but for Cd and Sn the ratio should be calculated from Eq. (8). The obtained results are further compiled in Table 3. It is evident that all the migrating species (Cu, Ag, Au and Zn) within the interstitial mechanism diffuse significantly faster along the c-axis than along the a-axis. In particular, the solute Cu exhibits a huge diffusion anisotropic ratio with a value as large as 5291.93 at the temperature of 300 K, which is significantly greater than those of Ag, Au and Zn. This fact is well consistent with the early experimental observation [41]. The origin of their faster diffusion along the c-axis can be attributed to the fact that along the c-axis of β -Sn there exists a straight tunnel of considerably larger size as marked by the purple lines in Fig.1. Apparently, if the interstitial solutes diffuse along this straight and open channel, there would not be any difficulty, in accordance with their extremely low migration energy barriers (see Table 1). On the other hand, we note that the diffusion pathways along the c-axis have the relative larger interstitial spacing, compared with those along the a-axis. Therefore, it is expected that the interatomic repulsive resistance along the c-axis channel would be much smaller than that along the a-axis channel. Moreover, it can be seen from Fig.3(a) that for the interstitial solute atoms diffusing through the a-axis they have to overcome a large energy barrier due to the strong strain at the saddle point. All these facts result in the lower diffusion activation energy barrier along the c-axis compared with that along the a-axis (see Table 1). However, for the solute Cd diffusion and the self-diffusion of Sn, their anisotropic ratio is not apparent because of their vacancy-mediated mechanism.

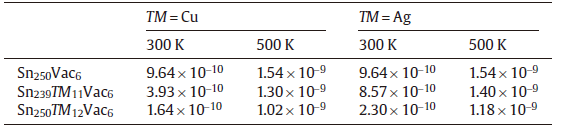
3.4. Effects of solutes on the self-diffusion of Sn

Once the diffusion mechanism is clarified, we transfer our attention on the effects of the solutes Cu and Ag on the self-diffusion of Sn. To this end, we have performed abMD simulations by considering three different supercells with the nearly same atomic concentration of Cu (or Ag) and vacancy at the temperatures of 300 K and 500 K. The first supercell is Sn250Vac6 containing six vacancies and no addition of the solute TM to simulate the Sn self-diffusion in pure β -Sn. The second supercell is Sn250TM12Vac6 in which twelve TM atoms dissolve interstitially in the lattice. The third supercell is Sn239TM11Vac6 with eleven TM atoms occupying the substitutional sites. Note that during our abMD simulations the solute atoms and vacancies are randomly introduced in the supercell and their atomic concentrations are nearly the same. We also need point out that the concentrations of the solute TM and vacancies used in our simulations are artificially set larger than their real equilibrium concentrations, for the sake of easily elucidating the effects of the solute TM on the self-diffusion of Sn. In addition, five initial configurations for each supercell have been taken into account to eliminate the initial configuration influence on the mean square displacement (MSD). Finally, the MSD of Sn atoms are computed by averaging over all the initial configurations and over all the Sn atoms. Then, the diffusion coefficient D could be obtained through a linear fitting to the dependence of average mean square displacement over 6t. As an example, Fig.5 shows the self-diffusivity of Sn atoms within the three different supercells as a function of time at the temperature of 500 K.

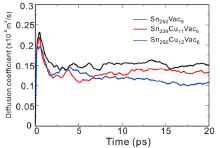Fig.5 Diffusion coefficient of Sn atoms within three different supercells as a function of time at the temperature of 500 K.

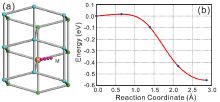
Table 4 listed the computed diffusion coefficients of Sn atom affected by the addition of Cu (or Ag) at 300 K and 500 K. It can be found that no matter where Cu (Ag) occupies, either substitutionally or interstitially, the addition of Cu (Ag) would reduce the self-diffusivity of Sn. The reduced effect becomes more remarkably for the interstitial solution of Cu (Ag). Moreover, the self-diffusivity of Sn is exceptionally hindered by Cu when compared to Ag. The reason can be ascribed to two aspects: (i) The substitutional Ag atoms would increase the diffusion energy barriers of its first-nearest-neighbor Sn atoms and thus decrease the self-diffusivity of Sn, which was already confirmed by the first-principles calculations[50]. Despite the low amount of substitutional solution, Cu exhibits the similar behavior but more pronouncedly[50]. (ii) From our abMD simulations, it has been found that the interstitially dissolved Cu (Ag) atoms would combine with vacancy and further annihilate the vacancy during the process of diffusion. This is also confirmed by our CI-NEB calculations. As shown in Fig.6, if one interstitial Cu atom diffuses in the presence of a nearby Sn-vacancy, it can be easily trapped with the vacancy without any energy barrier. Besides, the combination between the interstitial Cu atom and the vacancy would be more energetically stable. The similar phenomenon is also observed in the case of the interstitial Ag. Since the amount of vacancies is reduced by the interstitial Cu (Ag) atoms, the self-diffusivity of Sn, which is controlled by the vacancy-mediated mechanism, is hence greatly decreased. In addition, we also noted that besides the reduction of bulk self-diffusivity of Sn, Cu (Ag) also has the effects on reducing the grain boundary self-diffusivity of Sn[51]. Accordingly, the small addition of Cu (Ag) in β -Sn would apparently decrease the self-diffusivity of Sn, thus taking the action on prolonging the EM lifetime of the Sn-based solders.

Table.4 Self-diffusivity (D, m2/s) of Sn atoms calculated by abMD simulations for three different supercells at the temperature of 300 K and 500 K. The self-diffusivity of Sn at 500 K (about 3.00 × 10-9 m2/s) obtained by Mohamed et al.[49] is given for comparison purpose

Fig.6 (a) Schematic picture of the diffusion pathway for the interstitial Cu atom (pink ball) diffusing in the presence of a nearby Sn-vacancy (light red ball), and (b) the corresponding minimum energy path. The cyan and green balls in (a) represent the two different layers of β -Sn.

4. Conclusion

In conclusion, the site preferences and diffusion mechanisms of TM (TM = noble metals, Zn and Cd) in β -Sn as well as the self-diffusion of Sn, have been investigated through first-principles calculations and compared with the available experimental data. We have found that Cu prefers the interstices, while Cd and Sn are preferable in the substitutional sites. As for Ag, Au and Zn, although they are energetically stable in the substitutional sites, they are still able to dissolve partially interstitially due to their not too large interstitial solution enthalpies compared with the Sn-vacancy formation energy. Stain and electronic structure analysis evidence that the site preferences are governed by the solutes' size factor and the d-s hybridizations between the solute and the host Sn atom. Moreover, it has been deduced that all the noble metals and Zn diffuse mostly by the interstitial mechanism, while the self-diffusion of Sn is vacancy-mediated. No matter which mechanism does the Cd choose, the activation energies are both very high. That is the reason as to why the diffusion for the noble metals and Zn are significantly faster than that for Cd diffusion and Sn self-diffusion. It has also been found that the diffusivity can be correlated with the amount of interstitial solution, i.e., the more the mount of interstitial solution is, the faster the solute diffuses. The anisotropy of diffusion has also been discussed. The faster diffusion along the c-axis for noble metals and Zn diffusions can be attributed to the extremely low migration energy barrier caused by the straight tunnel of considerable size with the screw axis symmetry of 2π /4 along the c-axis. Furthermore, the effects of Cu (Ag) on the self-diffusion of Sn have been studied through the abMD simulations. Our results reveal that during the process of diffusion the interstitially dissolved Cu (Ag) atoms would combine with the Sn-vacancy and further annihilate the vacancy, which reduces the self-diffusion of Sn. The present work might provide an evidence to design good Sn-based solders with high electromigration resistance by the solutes enhancement method.

Acknowledgements Acknowledgments

This study was supported by the ‘Hundred Talents Project’ of the Chinese Academy of Sciences and from the Major Research Plan (Grant No. 91226204), the Key Research Program of Chinese Academy of Sciences (Grant No. KGZD-EW-T06), the National Natural Science Foundation of China (Grant Nos. 51474202 and 51174188) and the Beijing Supercomputing Center of CAS (including its Shenyang branch) as well as the high-performance computational cluster in the Shenyang National University Science and Technology Park.

The authors have declared that no competing interests exist.

Reference
[1] R. Ishikawa, R. Mishra, A. R. Lupini, S. D. Findlay, T. Taniguchi, S. T. Pantelides, S. J. Pennycook Phys. Rev. Lett, 113(2014), p. 155501 [本文引用:1]
[2] P. Liu, W. Xing, X. Cheng, D. Li, Y. Li, X. -Q. Chen Phys. Rev. B, 90(2014), p. 024103 [本文引用:2]
[3] N. Hall, J. H. Racette J. Appl. Phys, 35(1964), pp. 379-397 [本文引用:1]
[4] J. Ma, S. H. Wei Phys. Rev. Lett, 110(2013), p. 235901 [本文引用:2]
[5] H. L. Liu, X. Shi, F. F. Xu, L. L. Zhang, W. Q. Zhang, L. D. Chen, Q. Li, C. Uher, T. Day, G. J. Snyder Nat. Mater, 11(2012), pp. 422-425 [本文引用:1]
[6] K. J. Puttlitz K. J. Puttlitz, K. A. Stalter (Eds. ), Hand book of Lead-free Solder Technology for Microelectronic Assemblies, Marcel Dekker, Inc. , New York (2004), pp. 239-280 [本文引用:1]
[7] P. S. Ho, T. Kwok Rep. Prog. Phys, 52(1989), pp. 301-348 [本文引用:1]
[8] K. N. Tu J. Appl. Phys, 94(2003), pp. 5451-5473 [本文引用:1]
[9] C. Y. Liu, C. Chen, K. N. Tu J. Appl. Phys, 88(2000), pp. 5703-5709 [本文引用:1]
[10] Y. C. Hu, Y. H. Lin, C. R. Kao, K. N. Tu J. Mater. Res, 18(2003), pp. 2544-2548 [本文引用:1]
[11] Y. T. Yeh, C. K. Chou, Y. C. Hsu, C. Chen, K. N. Tu Appl. Phys. Lett, 86(2005), p. 203504 [本文引用:1]
[12] B. Chao, S. H. Chae, X. Zhang, K. H. Lu, J. Im, P. S. Ho Acta Mater, 55(2007), pp. 2805-2814 [本文引用:2]
[13] S. H. Chae, X. Zhang, K. H. Lu, H. L. Chao, P. S. Ho, M. Ding, P. Su, T. Uehling, L. N. Ramanathan J. Mater. Sci. Mater. Electron, 18(2006), pp. 247-258 [本文引用:1]
[14] T. L. Shao, Y. H. Chen, S. H. Chiu, C. Chen J. Appl. Phys, 96(2004), pp. 4518-4524 [本文引用:1]
[15] L. T. Chen, C. M. Chen J. Mater. Res, 21(2011), pp. 962-969 [本文引用:1]
[16] T. Y. Lee, K. N. Tu, D. R. Frear J. Appl. Phys, 90(2001), pp. 4502-4508 [本文引用:3]
[17] J. D. Wu, W. Lee, Y. Wu, S. Li Proceedings of the 42nd Annual International Reliability Physics Symposium, Phoenix IEEE, New York (2004), pp. 565-566 [本文引用:1]
[18] H. B. Huntington, A. R. Grone J. Phys. Chem. Solids, 20(1961), pp. 76-87 [本文引用:1]
[19] J. P. Dekker, P. Gumbsch, E. Arzt Phys. Rev. B, 59(1999), pp. 7451-7457 [本文引用:1]
[20] P. Hohenberg, W. Kohn Phys. Rev, 136(1964), pp. B864-B871 [本文引用:1]
[21] W. Kohn, L. J. Sham Phys. Rev, 140(1965), pp. A1133-A1138 [本文引用:1]
[22] G. Kresse, J. Hafner Phys. Rev. B, 47(1993), pp. 558-561 [本文引用:1]
[23] G. Kresse, J. Furthmuller Phys. Rev. B, 54(1996), pp. 11169-11186 [本文引用:1]
[24] P. E. Blöchl Phys. Rev. B, 50(1994), pp. 17953-17979 [本文引用:1]
[25] J. P. Perdew, K. Burke, M. Ernzerhof Phys. Rev. Lett, 77(1996), pp. 3865-3868 [本文引用:1]
[26] H. J. Monkhorst, J. D. Pack Phys. Rev. B, 13(1976), pp. 5188-5192 [本文引用:1]
[27] D. Sheppard, P. Xiao, W. Chemelewski, D. D. Johnson, G. Henkelman J. Chem. Phys, 136(2012), p. 074103 [本文引用:1]
[28] S. Nosé J. Chem. Phys, 81(1984), pp. 511-519 [本文引用:1]
[29] H. Mehrer Diffusion in Solids: Fundamentals, Methods, Materials, Diffusion-controlled Processes Springer, Germany(2007), pp. 58-60 [本文引用:1]
[30] J. F. Nicholas Acta Metall, 3(1955), pp. 178-181 [本文引用:1]
[31] J. Miller, D. Gemmell, R. Holland , J. Poizat, J. Worthington, R. Loess Phys. Rev. B, 11(1975), pp. 990-994 [本文引用:4]
[32] G. Hägg Z. Phys. Chem, 8(1930), pp. 455-474 [本文引用:2]
[33] B. F. Dyson, T. R. Anthony, D. Turnbull Bull. Am. Phys. Soc, 10(1965), p. 1094 [本文引用:2]
[34] B. F. Dyson, T. R. Anthony, D. Turnbull J. Appl. Phys, 37(1966), pp. 2370-2374 [本文引用:2]
[35] F. Frank, D. Turnbull Phys. Rev, 104(1956), pp. 617-618 [本文引用:2]
[36] T. R. Anthony, D. Turnbull Phys. Rev, 151(1966), pp. 495-498 [本文引用:2]
[37] M. Dariel, L. Kornblit, B. Beaudry, K. Gschneidner Phys. Rev. B, 20(1979), pp. 3949-3956 [本文引用:2]
[38] T. R. Anthony, D. Turnbull Appl. Phys. Lett, 8(1966), pp. 120-121 [本文引用:1]
[39] C. W. Mao Phys. Rev. B, 5(1972), pp. 4693-4704 [本文引用:1]
[40] B. F. Dyson J. Appl. Phys, 37(1966), pp. 2375-2377 [本文引用:2]
[41] B. F. Dyson J. Appl. Phys, 38(1967), pp. 3408-3409 [本文引用:4]
[42] F. Huang, H. Huntington Phys. Rev. B, 9(1974), pp. 1479-1488 [本文引用:4]
[43] C. Coston, N. H. Nachtrieb J. Phys. Chem, 68(1964), pp. 2219-2229 [本文引用:6]
[44] N. L. Peterson, F. Seitz, D. Turnbull, H. Ehrenreich (Eds. ), Solid State Physics, vol. 22, Academic Press, New York(1968), pp. 409-512 [本文引用:3]
[45] M. B. Dutt, B. L. Sharma Diffusion in Semiconductors Non-metallic Solids
Springer-Verlag, Berlin(2003), pp. 334-335 [本文引用:2]
[46] D. Berger, W. Lange Phys. Status Solidi (B), 18(1966), pp. 67-74 [本文引用:1]
[47] A. Ascoli, G. Poletti Phys. Rev. B, 6(1972), pp. 3681-3684 [本文引用:1]
[48] A. D. Le Claire Acta Metall, 1(1953), pp. 438-447 [本文引用:1]
[49] M. Mouas, J. G. Gasser, S. Hellal, B. Grosdidier, A. Makradi, S. Belouettar EPJ Web Conf, 15(2011), p. 01013 [本文引用:1]
[50] C. Yu, H. Lu J. Appl. Phys, 102(2007), p. 054904 [本文引用:2]
[51] M. S. Sellers, A. J. Schultz, C. Basaran, D. A. Kofke J. Appl. Phys, 110(2011), p. 013528 [本文引用:1]