Study on Dendritic Growth in Pressurized Solidification of Mg-Al Alloy Using Phase Field Simulation

Cite this Article

Haowei Pan, Zhiqiang Han, Baicheng Liu. Study on Dendritic Growth in Pressurized Solidification of Mg-Al Alloy Using Phase Field Simulation. Journal of Materials Science & Technology, 2016, 32(1): 68-75 Copy to clipboard

Permissions

Received:2015-04-09

Study on Dendritic Growth in Pressurized Solidification of Mg-Al Alloy Using Phase Field Simulation

Haowei Pan¹, Zhiqiang Han¹, Baicheng Liu^1,²

¹ Key Laboratory for Advanced Materials Processing Technology, Ministry of Education, School of Materials Science and Engineering, Tsinghua University, Beijing 100084, China

² State Key Laboratory of Automotive Safety and Energy, Department of Automotive Engineering, Tsinghua University, Beijing 100084, China

Corresponding author. Tel.: +86 10 62794616; Fax: +86 10 62794616. E-mail address: zqhan@tsinghua.edu.cn (Z. Han).

Abstract

A multi-grain phase field model coupled with thermodynamic calculation was adopted to describe the dendritic growth in pressurized solidification of Mg-Al alloy during squeeze casting, in which the effects of the pressure on the Gibbs free energy and chemical potential of solid and liquid phases, the solute diffusion coefficient, and the solute partition coefficient were considered. The individual effect of solute diffusion coefficient, and the Gibbs free energy on the dendritic growth was studied. With the comparison of the dendritic growth under atmospheric and elevated pressures, the effect of pressure on the microstructure evolution was discussed. The results showed that the grains are refined, the dendritic growth rate tends to increase and the secondary dendrite arms are more developed as the pressure is increased from 0.1 to 100 MPa, which showed a good agreement with the experimental results of direct squeeze casting of Mg-Al alloy. As the pressure increases, the largest dendritic growth rate can be obtained under the pressure between 200 and 250 MPa, while the growth rate decreases with a further increase of pressure.

Keyword: Phase field; Pressurized solidification; Dendritic growth; Mg-Al alloy; Gibbs free energy

Show Figures

1. Introduction

The use of Mg-Al alloy is proved to be a good way to realize lightweighting of automobiles, coping with the ever growing strict requirements of environment protection. With most of Mg-Al alloy manufactured by high pressure die-casting, it is restricted to produce thin and non-structural components due to the micro porosity defect. Squeeze casting diminishes this defect, which expands the usage of Mg-Al alloy due to the higher integrity and better mechanical properties of products^[1]. As metal is solidified under pressure in squeeze casting, pressure is essential for the nucleation^[2] and growth process^[3] of microstructure evolution, which exerts influence on the mechanical properties. Thus, to understand the solidification mechanism under pressure is of great significance to the design and optimization of squeeze casting process.

Experimental studies on microstructure evolution in pressurized solidification have been carried out for years. In the pressure range of several GPa, the phase diagrams of alloys are significantly changed, which exerts a great influence on solidification^[4]. The superhigh pressure increases the nucleation density and decreases the solute diffusion coefficient, resulting in fine microstructure^[5] and high solid solubility^{[6, 7]}. In the pressure range of squeeze casting, more focus has been put on the enhancement of heat transfer between the casting and the mold due to the applied pressure^{[8, 9, 10]}. The pressure reduces the air gap between the casting and the mold during solidification, which increases the cooling rate and results in the refinement of grain size^[11]. The influence of process parameters on microstructure and mechanical properties has also been studied^[12].

To better understand the microstructure evolution process, numerical modeling and simulation methods such as cellular automaton and phase field have been applied to investigate into the dendritic growth during solidification^{[13, 14, 15]}. Huo et al. developed a cellular automaton model with two sets of mesh to simulate equiaxed grain growth and columnar grain growth in directional solidification of Mg-Al alloy^{[16, 17, 18]}. Bö ttger et al.^{[19, 20]} conducted simulation of equiaxed solidification of Mg-Al alloy based on phase field method. However most of these models are for solidification process under atmospheric pressure, and there are limited simulation models for pressurized solidification. Li et al.^[21] simulated microstructure and micro segregation under pressure using cellular automaton method, in which the pressure was applied in only one direction, which is not comparable with real condition. Bö rzsö nyi et al.^{[22, 23]} investigated the effects of time-periodic external forcing on dendritic growth of CCH₃, a kind of liquid crystal, by experiments and phase field modeling, and found that the oscillating pressure and heating can tune the frequency of dendritic side-branching, indicating that thermal and mechanical effects are two dominant factors in interface stability. For pressurized solidification, the pressure changes the solute diffusion condition and the free energy of various phases^[24], both of which impact the microstructure evolution. Phase field models are thermodynamically consistent^[25] based on energy description of alloy systems, thus a phase field model taking the effect of pressure on solute diffusion and free energy of various phases into account is promising to simulate the microstructure evolution under pressure.

In this study, a multi-grain phase field model coupled with thermodynamic calculation is adopted to describe the dendritic growth of Mg-Al alloy during squeeze casting. In the model, the effects of pressure on the Gibbs free energy of solid and liquid phases, the solute diffusion coefficient and the solute partition coefficient are taken into consideration. The overall effect of 100 MPa pressure on the dendritic growth is studied and the results are compared with experiment. To illustrate the effects of the solute diffusion coefficients in liquid, and the Gibbs free energy of liquid and solid phases on dendritic growth, several simulation cases with different parameters are conducted.

2. Model Description

2.1. Phase field model

The total free energy of the alloy system is defined as^[26]

$F = \int_{Ω} [[f (ϕ, c) + \frac{1}{2} ε^{2} {| \nabla \emptyset |}^{2}]] d Φ$ (1)

where f is the chemical free energy density, ε is the gradient energy coefficient related to the interface anisotropy and ϕ is the phase field, which is defined as ϕ =0 in the bulk liquid, ϕ =1 in the bulk solid and 0< ϕ < 1 in the interfacial region. The free energy density is defined as

f(ϕ , c)=h(ϕ )fS(c_S)+[1-h(ϕ )]fL(c_L)+wg(ϕ ) (2)

where fS(c_S) and fL(c_L) are the free energy densities of the homogeneous solid and liquid phases, respectively. As for the interpolation function, we choose

h(ϕ )=ϕ ³(6ϕ ²-15ϕ +10) (3)

g(ϕ )=ϕ ²(1-ϕ )²(4)

The interface region is defined as a mixture of solid and liquid with compositions different from each other, while restricted by the equal chemical potential condition based on KKS model^[26]:

$f_{CS}^{S} [C_{S} (x, t)] = f_{CS}^{L} [C_{L} (x, t)]$ (5)

To develop a phase field model for multi-grain simulation, an orientational field is introduced into the model instead of adopting multi-phase field model^[27]. The non-conserved orientational field variable ϑ determines the grain orientation in the reference frame, which is set to 0 in the liquid but has a definite value between 0 and 1 in the grain. The orientational contribution to the free energy density f_ori=Hh(ϕ )|∇ϑ | depicts the excess energy of inhomogeneities in grain orientation, in which the parameter H represents the energetic cost of misorientation. h(ϕ ) varies smoothly from 0 to 1 as ϕ changes from the liquid to solid, so that the excess energy acts only in the solid. The governing equations for the phase field, the orientational field and the concentration field are given as follows^[27]:

$\frac{\partial \emptyset}{\partial t} = - M_{\emptyset} \frac{δF}{δ∅} = M_{\emptyset} (ε^{2} \nabla^{2} \emptyset - Hh' (\emptyset) | \nabla ϑ | - f_{\emptyset})$ (6)

$\frac{\partial ϑ}{\partial t} = M_{\emptyset} H \nabla [h (\emptyset) \frac{\nabla ϑ}{| \nabla ϑ |}]$ (7)

$\frac{\partial C}{\partial t} = \nabla [D (\emptyset) \nabla C] + \nabla [D (\emptyset) h' (\emptyset) (C_{L} - C_{S}) \nabla \emptyset]$ (8)

Parameters in the phase field equations are the phase field mobility M_ϕ, the orientation field mobility M_ϑ, the gradient energy coefficient ε and the height of the parabolic potential w. The gradient energy coefficient and the height of the parabolic potential are determined by the interface energy σ and the interface width 2λ . Based on the one-dimension equilibrium solution, the parameters of the phase field can be given as follows^[28]

$ε = \sqrt[]{\frac{6 λσ}{α}}$ (9)

$w = \frac{3 ασ}{λ}$ (10)

where α is a constant, which is dependent on the definition of the interface thickness. In this work, we define that in the interface region, ϕ changes from 0.05 to 0.95 at-λ < x< +λ , then α ≈ 2.94^[28]. According to Echebarria et al.^[29], the interface width should be smaller than physical relevant length scale of the problem concerned, which in solidification is the tip radius for dendritic growth. In our work, the interface is described by 4 layers of grids, i.e. 2λ =4Δ x, where Δ x is the grid size. The phase field mobility M_ϕ is related to the interface kinetics, which is given as^[28]

$\frac{1}{M_{\emptyset}} = \frac{ε^{3}}{D (\emptyset) σ \sqrt[]{2 w}} ξ (C_{L}^{e}, C_{S}^{e})$ (11)

$ξ (C_{L}^{e}, C_{S}^{e}) = f_{CC}^{S} (C_{S}^{e}) f_{CC}^{L} (C_{L}^{e}) {(C_{L}^{e} - C_{S}^{e})}^{2} \times \int_{0}^{1} \frac{h (\emptyset) [1 - h (\emptyset)] d∅}{[1 - h (\emptyset)] f_{CC}^{S} (C_{S}^{e}) + h (\emptyset) f_{CC}^{L} (C_{L}^{e}) \emptyset (1 - \emptyset)}$ (12)

The anisotropy is introduced into the interface energy and the gradient energy coefficient, which is shown below^[30],

$σ (θ) = \overset{̅}{σ} [1 + γ \cos (ηθ - 2 πϑ)]$ (13)

$ε (θ) = \overset{̅}{ε} [1 + γ \cos (ηθ - 2 πϑ)]$ (14)

where $\overset{̅}{σ}$ , $\overset{̅}{ε}$ are the isotropic interface energy and gradient energy coefficient, respectively and γ is the anisotropy strength. For Mg-Al alloy the usual choice of sixfold anisotropy is adopted, which means η =6. θ is the angle between the normal to the interface pointing to the liquid and the horizontal direction shown as Eq. (15). 2π ϑ /η represents the angle between the crystallographic axis and the x-axis.

$θ = \arctan (\frac{ϕ_{y}}{ϕ_{x}})$ (15)

To the best of authors' knowledge, the reports on the effect of pressure on the interface energy of Mg-Al alloy are quite limited. Luo et al.^[31] and Zhang et al.^[32] studied the effect of pressure on the interface energy of Ni and Co by using molecular dynamics, respectively. The results showed that under the pressure of 100 MPa, which is usually the pressure used in squeeze casting, the effect of pressure on the interface energy is insignificant. The interface energy of Mg-Al alloy under the pressure of squeeze casting is regarded as the same as that under atmospheric pressure in this study.

2.2. Thermodynamics and Gibbs free energy under pressure

The Gibbs free energy for each phase of Mg-Al alloy can be described by Redlich-Kister equation as follows^[33]:

$G_{m}^{φ} = X_{AI} G_{Al}^{φ} + X_{Mg} G_{mg}^{φ} + RT (X_{AI} \ln X_{AI} + X_{Mg} \ln X_{Mg}) +^{ex} G_{m}^{φ}$ (16)

where $G_{Al}^{φ}$ and $G_{mg}^{φ}$ are the Gibbs free energy of pure Al and Mg in the phase of φ , respectively. $X_{AI}$ and $X_{Mg}$ are the molar fractions of Al and Mg and R is the gas constant. The excess energy of mixing is given as follows^[33]:

${}^{ex}{G_{m}^{ϕ} = X_{AI} X_{Mg} \sum_{j}^{=} {}^{J}{L_{Al, Mg}^{ϕ} {(X_{AI} - X_{Mg})}^{j}}}$ (17)

^jL_{Al, Mg}=^jA+^jBT (18)

The parameters A and B are referred to the thermodynamic description of the Mg-Al system from Saunders^[34]. The Gibbs free energy under pressure is calculated based on the quasi-harmonic approximation and equation of state (EOS)^[35] as follows:

$G (T, P) = G (T, P_{0}) + \int_{P_{0}}^{P} V (T, P') dP'$ (19)

where G is the Gibbs free energy and P₀ is the reference pressure. To calculate the Gibbs free energy under a specific temperature and pressure starting at a reference point, the integration path in Fig. 1 suggested by Brosh^[36] is adopted, which takes the advantage that the isobaric heat capacity converges to the isochoric heat capacity at the limit of infinite pressure:

$C_{P} (P \to \infty) = C_{V} (P \to \infty)$ (20)

	Figure Option View Download New Window
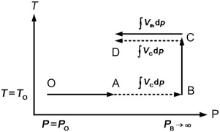	Fig. 1. Integration path for Gibbs free energy calculation^[34].

The volume in Eq. (19) is composed of two terms, where V_c(P) is the “ cold compression curve” and V_th(P, T) the “ thermal volume” .

V(P, T)=V_c(P)+V_th(P, T) (21)

The expression for the Gibbs free energy at point D is the sum of the integrals over the paths OA, BC and CD, where in CD, only the thermal volume V_th(P, T) is included in the integrand, as the cold compression curve is canceled out with the integral over the path AB. More details of the calculation method can be found in Ref. ^[36].

2.3. Solute diffusion coefficient under pressure

As the viscosity of the melt increases with the increase of pressure, based on the equation describing the effect of pressure on diffusion coefficient shown as follows, the solute diffusion coefficient is affected by the pressure significantly^[37].

$D^{P} = RT δ^{- 1} η_{P}^{- 1} = RT δ^{- 1} η_{0}^{- 1} \exp (- P V_{0} / RT)$ (22)

where δ is the length of free journey for the atom, η _P is the viscosity of the melt under elevated pressure, η ₀ is the viscosity of the melt under atmospheric pressure, and V₀is the molar volume of the liquid phase. The solute diffusion coefficient under pressure can be calculated as follows, where D₀ represents the solute diffusion coefficient under atmospheric pressure. It can be seen that the solute diffusion coefficient decreases exponentially with the increasing pressure.

$D^{P} = D_{0} \exp (- P V_{0} / RT)$ (23)

2.4. Solute partition coefficient

The common tangent of Gibbs free energy method^[38] is applied to calculate the equilibrium solute concentration and the partition coefficient of Mg-Al alloy in squeeze casting. First the Gibbs free energy of the solid and liquid phases under pressure is calculated with the method discussed above and then the common tangent method is applied. As illustrated in Fig. 2, $g_{P}^{S}$ and $g_{P}^{L}$ are the molar Gibbs free energy of the solid and liquid phases under pressure, respectively. Other simulation parameters for Mg-Al alloy used in the simulation are given in Table 1.

	Figure Option View Download New Window
	Fig. 2. Schematic of the common tangent method for equilibrium concentration calculation.

Table 1 Parameters used in the simulation of Mg-Al binary alloy

3. Simulation Results and Discussion

3.1. Effect of solute diffusion coefficient on dendritic growth

Eq. (23) implies that as the applied pressure increases, the solute diffusion coefficient decreases. The individual effect of solute diffusion coefficient in liquid on the dendritic growth is shown in Fig. 3. Case studies were conducted under isothermal condition with T = 851 K, in which the solute diffusion coefficients in liquid were 1.5 × 10^-9, 2.0 × 10^-9, 2.5 × 10^-9, and 3.0 × 10^-9m²/s, respectively. These solute diffusion coefficients correspond to the solidification condition under the pressures of 400 MPa, 300 MPa, 100 MPa and 0.1 MPa, respectively. It is shown in Fig. 3(b) that as the solute diffusion coefficient increases, the dendritic growth rate increases, where the dendritic growth rate is given as the dendritic tip velocity.

	Figure Option View Download New Window
	Fig. 3. Calculated dendritic growth with different solute diffusion coefficient in liquid: (a) dendritic growth rate with time, (b) dendritic growth rate with diffusion coefficient.

With the decrease of solute diffusion coefficient, the solute rejected due to the transformation from liquid to solid phase cannot efficiently diffuse to the bulk liquid and accumulates in the front of the liquid-solid interface, resulting in the reduction of the dendritic growth rate, as shown in Fig. 3(b).

3.2. Effect of Gibbs free energy on dendritic growth

Based on the model of Brosh^[36], the Gibbs free energy of solid and liquid phases of Mg-Al alloy under atmospheric and elevated pressures is depicted in Fig. 4. It can be seen that the Gibbs free energy of both liquid and solid phases increases with the increase of pressure. For the whole range of Al fraction, the Gibbs free energy for both liquid and solid phases is about 10% higher under 100 MPa than that under atmospheric pressure.

	Figure Option View Download New Window
	Fig. 4. Calculated Gibbs free energy of Mg-Al alloy under various pressures: (a) liquid phase, (b) solid phase.

According to the research of Kim et al.^[28] and Qin and Wallach^[39], in the phase field simulation, the phase field driving force of the system is defined as

$R = f^{L} (C_{L}) - f^{S} (C_{S}) - f_{c}^{L} (C_{L}) (C_{L} - C_{S})$ (24)

The phase field driving force is proportional to the thermodynamic driving force. As the applied pressure is increased, the Gibbs free energy of both liquid and solid phases of Mg-Al alloy is enhanced, resulting in the enhanced difference between the Gibbs free energy of liquid and solid phases. According to Eq. (24), the thermodynamic driving force is mainly dependent on the difference between the Gibbs free energy of liquid and solid phases, and it is increased under elevated pressure. From this perspective, the applied pressure expedites the dendritic growth. The individual effect of the changed Gibbs free energy on the dendritic growth is shown in Fig. 5, where only the effect of pressure on the Gibbs free energy is considered. It can be seen from Fig. 5(b) that within the pressure range from 0.1 to 100 MPa, the dendritic growth rate increases almost linearly with the applied pressure, when only the change of Gibbs free energy with pressure is taken into account.

	Figure Option View Download New Window
	Fig. 5. Calculated dendritic growth under different pressure when only the effect of pressure on the Gibbs free energy was considered: (a) dendritic growth rate with time, (b) dendritic growth rate with pressure.

3.3. Overall effect of pressure on dendritic growth

As is discussed above, the applied pressure reduces the solute diffusion coefficient, which hinders the dendritic growth, meanwhile enhances the difference between the Gibbs free energy of liquid and solid phases of Mg-Al alloy, which enlarges the driving force and expedites the dendritic growth. Taking the effects of pressure on both parameters into consideration, the isothermal simulation with T = 851 K is carried out. The results of microstructure of Mg-Al alloy under atmospheric and 100 MPa pressure are shown inFig. 6, where Δ t is the simulation time step. It can be seen from Fig. 6 that the dendritic growth rate under 100 MPa tends to increase compared with that under atmospheric pressure, and the secondary dendrite arms are more developed. At the same simulation time of t = 10, 000Δ t, the primary dendrite arm length under 100 MPa is larger than that under atmospheric pressure. Together with the more developed secondary dendrite arms, it indicates that the solid fraction of the simulation domain also increases significantly. Due to the increased dendritic growth rate and the decreased solute diffusion coefficient, the solute rejected from the transformation from liquid to solid phase accumulates at the roots of the dendrite arms, which enhances the branch of microstructure.

	Figure Option View Download New Window
	Fig. 6. Phase field profile for the dendritic growth at t = 10, 000Δ t: (a) under atmospheric pressure, (b) under 100 MPa.

To show the effect of pressure on dendritic growth more clearly and to simulate the process of squeeze casting, the pressure is applied at a certain time after the start of solidification, as is the case in squeeze casting. The Mg-Al alloy system is first solidified under atmospheric pressure and then at t = 10, 000Δ t the pressure of 100 MPa is applied, changing the thermodynamics and solute diffusion coefficient of the system. The phase field profiles from t = 10, 000Δ t to t = 16, 000Δ t with an interval of 2000Δ t are shown in Fig. 7.

	Figure Option View Download New Window
	Fig. 7. Phase field profile at (a) t = 10, 000Δ t, (b) t = 12, 000Δ t, (c) t = 14, 000Δ t and (d) t = 16, 000Δ t for the dendritic growth process with the pressure of 100 MPa applied at t = 10, 000Δ t.

The dendritic growth rates of solidification at first under atmospheric pressure and then under 100 MPa can be deduced from Fig. 8. Under atmospheric pressure the dendritic growth rate remains a constant value, and after the introduction of the pressure of 100 MPa, it becomes higher about 20% showing that the overall effect of pressure enhances the dendritic growth rate of Mg-Al alloy.

	Figure Option View Download New Window
	Fig. 8. Simulated result of the coordinate of dendrite tip with simulation time during the dendritic growth process with the pressure of 100 MPa applied at t = 10, 000Δ t.

As shown in Fig. 7, when the pressure is applied, the primary dendrite arms become slimmer while the secondary dendrite arms tend to be more developed. In squeeze casting, the pressure is applied at a certain time after the melt is poured into the mold, so the melt is first solidified under atmospheric pressure and then under elevated pressure. From the comparison of the morphology of typical dendrites under atmospheric and 100 MPa pressure shown in Fig. 9, the primary dendrite arms under atmospheric pressure are bolder than that under elevated pressure. As for the microstructure under 100 MPa, the roots of the primary dendrite arms are bold as this part is solidified under atmospheric pressure, while with the pressure applied, the primary dendrite arms become slimmer and the secondary dendrite arms are more developed. The simulation results agree well with the experiment as compared Fig. 7 with Fig. 9.

	Figure Option View Download New Window
	Fig. 9. Dendritic morphology of Mg-Al alloy observed using optical microscope: (a) cast under atmospheric pressure, (b) cast under 100 MPa.

To give a broader view of the effect of pressure on dendritic growth, solidification simulations of Mg-Al alloy under different pressures were conducted, and the results are shown in Fig. 10. The opposite effects of pressure on dendritic growth due to the enhanced driving force of dendritic growth and decreased solute diffusion coefficient lead the dendritic growth rate at first increase and then decrease with respect to the applied pressure. The highest growth rate can be achieved between the pressure of 200 and 250 MPa. In the pressure range from 0.1 to 200 MPa, the contribution of the increased driving force to the dendritic growth prevails, which expedites the dendritic growth. When the pressure is larger than 250 MPa, the effect of the decreased solute diffusion coefficient is dominant, which hinders the dendritic growth. As for industrial squeeze casting the applied pressure is usually lower than 200 MPa, so the dendritic growth rate increases with the applied pressure.

	Figure Option View Download New Window
	Fig. 10. Calculated dendritic growth rate under different pressures.

3.4. Multi-grain simulation

Han et al.^[2] studied the effect of pressure on the nucleation rate of Al alloy A356 and showed that for an industrial squeeze casting process with the applied pressure in the range from 80 to 100 MPa, increasing the applied pressure significantly increases the nucleation rate. Based on the nucleation model under pressure developed by Han et al. and our previous experimental study on squeeze casting of AZ91 Mg alloy^[40], the dependence of nucleation rate of Mg-Al alloy on undercooling and pressure is calculated and shown in Fig. 11. It can be seen that the peaks of nucleation rate corresponds to the undercooling ranging from 30 to 35 K. As the undercooling in industrial squeeze casting process is usually less than 20 K, the nucleation rate increases with the applied pressure, and the increased nucleation rate contributes to the refinement of the grain.

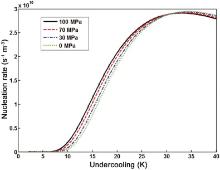	Figure Option View Download New Window
	Fig. 11. Nucleation rate with various undercoolings under selected pressures.

To calculate the nucleation density in 2D simulation, Poisson-Voronoi model^[41] is adopted, which is shown as follows, where N_V is the nucleation density in three dimensional space and N_S is the nucleation density in two dimensional space.

$N_{V} = 0.568 {(N_{S})}^{3 / 2}$ (25)

According to the calculated nucleation rate, 6 crystal nuclei and 12 crystal nuclei were seeded in the simulation domain under atmospheric pressure and 100 MPa, respectively. The simulation results are shown in Fig. 12, in which different colors represent different dendrite growing orientations. It can be seen that the dendrites grow up full of the domain and they impinge with each other as they grow. The solute rejected from the solidified grain accumulates at the interface of impinging arms, which hinders the growth of the dendritic growth as the solute enrichment decreases the undercooling. Fig. 13 shows the observed microstructure using optical microscope under polarized light of Mg-Al alloy solidified under atmospheric pressure and 100 MPa, respectively. The grain size of the solidified microstructure under atmospheric pressure and 100 MPa are measured as about 700 and 300 µ m, respectively. The simulation results agree well with the experimental microstructure.

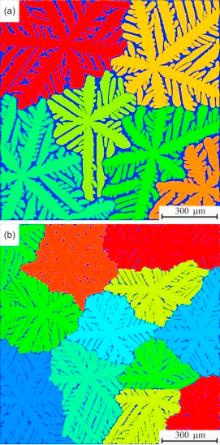	Figure Option View Download New Window
	Fig. 12. Multi-grain simulation result: (a) under atmospheric pressure, (b) under 100 MPa.

	Figure Option View Download New Window
	Fig. 13. Microstructure of Mg-Al alloy observed using optical microscope under polarized light: (a) under atmospheric pressure, (b) under 100 MPa.

4. Conclusions

A multi-grain phase field model coupled with thermodynamic calculation is adopted to describe the dendritic growth in pressurized solidification of Mg-Al alloy during squeeze casting, in which the effects of the pressure on the Gibbs free energy and chemical potential of solid and liquid phases, the solute diffusion coefficient, and the solute partition coefficient were considered.

The simulation results showed that the grains are refined, the dendritic growth rate tends to increase and the secondary dendrite arms are more developed as the pressure is increased from 0.1 to 100 MPa, which showed a good agreement with the experimental results of direct squeeze casting of Mg-Al alloy.

As the pressure increased, the driving force of dendritic growth increased, which expedited the dendritic growth, while the solute diffusion coefficient decreased, which hindered the dendritic growth. The opposite effects led the dendritic growth rate first increase and then decrease with pressure. The largest dendritic growth rate was achieved under the pressure between 200 and 250 MPa.

Acknowledgements Acknowledgments

This work was funded by the National Natural Science Foundation of China (Grant No.51175291), Tsinghua University Initiative Scientific Research Program (Grant No.2011Z02160), and the State Key Laboratory of Automotive Safety and Energy, Tsinghua University under the contract 2013XC-A-01.

The authors have declared that no competing interests exist.

Reference

View Option

[1]	M. R. Ghomashchi, A. Vikhrov J. Mater. Process. Technol, 101(2000), pp. 1-9 [本文引用:1]
[2]	Z. Q. Han, X. R. Huang, A. A. Luo, A. K. Sachdev, B. C. Liu Scr. Mater, 66(2012), pp. 215-218 [本文引用:2]
[3]	C. S. Goh, K. S. Soh, P. H. Oon, B. W. Chua Mater. Des, 31(2010), pp. S50-S53 [本文引用:1]
[4]	X. F. Yu, G. Z. Zhang, X. Y. Wang, Y. Y. Gao, G. L. Jia, Z. Y. Hao J. Mater. Sci, 34(1999), pp. 4149-4152 [本文引用:1]
[5]	S. S. Zhao, Q. M. Peng, H. Li, B. Z. Liu J. Alloy. Compd, 584(2014), pp. 56-62 [本文引用:1]
[6]	H. M. Kagaya, T. Suzuki, M. S. Takaya, T. Soma Physica B, 293(2001), pp. 343-346 [本文引用:1]
[7]	J. C. Jie, C. M. Zou, H. W. Wang, B. Li, Z. J. Wei Scr. Mater, 64(2011), pp. 588-591 [本文引用:1]
[8]	Z. Z. Sun, H. Hu, X. P. Niu J. Mater. Process. Technol, 211(2011), pp. 1432-1440 [本文引用:1]
[9]	K. M. Amin, N. A. Mufti J. Mater. Process. Technol, 212(2012), pp. 1631-1639 [本文引用:1]
[10]	J. H. Lee, H. S. Kim, C. W. Won, B. Cantor Mater. Sci. Eng. A, 338(2002), pp. 182-190 [本文引用:1]
[11]	M. T. Abou El-khair Mater. Lett, 59(2005), pp. 894-900 [本文引用:1]
[12]	M. S. Yong, A. J. Clegg J. Mater. Process. Technol, 145(2004), pp. 134-141 [本文引用:1]
[13]	K. Reuther, M. Rettenmayr Comput. Mater. Sci, 95(2014), pp. 213-220 [本文引用:1]
[14]	B. C. Liu, Q. Y. Xu, T. Jing, H. F. Shen, Z. Q. Han JOM, 63(2011), pp. 19-25 [本文引用:1]
[15]	A. Choudhury, K. Reuther, E. Wesner, A. August, B. Nestler, M. Rettenmayr Comput. Mater. Sci, 55(2012), pp. 263-268 [本文引用:1]
[16]	L. Huo, Z. Q. Han, B. C. Liu Acta Metall. Sin, 45 (2009), pp. 1414-1420 in Chinese [本文引用:1]
[17]	L. Huo, Z. Q. Han, B. C. Liu THERMEC, 638-842(2010), pp. 1562-1568 [本文引用:1]
[18]	L. Huo, Z. Q. Han, Z. Y. Liu, B. C. Liu PRICM, 561-565(2007), pp. 1797-1800 [本文引用:1]
[19]	B. Böttger, J. Eiken, M. Ohno, G. Klaus, M. Fehlbier, R. Schmid-Fetzer, I. Steinbach Adv. Eng. Mater, 8(2006), pp. 241-247 [本文引用:1]
[20]	B. Böttger, J. Eiken, I. Steinbach Acta Mater, 54(2006), pp. 2697-2704 [本文引用:1]
[21]	Q. Li, Q. Y. Guo, R. D. Li J. Univ. Sci. Technol. B. , 13(2006), pp. 516-522 [本文引用:1]
[22]	T. Börzsönyi, T. Tóth-Katona, A. Buka, L. Gránásy Phys. Rev. Lett, 83(1999), pp. 2853-2856 [本文引用:1]
[23]	T. Börzsönyi, T. Tóth-Katona, A. Buka, L. Gránásy Phys. Rev. E, 62(2000), pp. 7817-7827 [本文引用:1]
[24]	T. Hammerschmidt, I. A. Abrikosov, D. Alfè, S. G. Fries, L. Höglund, M. H. G. Jacobs, J. Koßmann, X. G. Lu, G. Paul Phys. Status Solidi B, 251(2014), pp. 81-96 [本文引用:1]
[25]	R. Spatschek, B. Eidel Int. J. Solids Struct, 50(2013), pp. 2424-2436 [本文引用:1]
[26]	S. G. Kim, W. T. Kim, T. Suzuki Phys. Rev. E, 58(1998), pp. 3316-3323 [本文引用:2]
[27]	J. J. Li, J. C. Wang, Q. Xu, G. C. Yang Acta Mater, 55(2007), pp. 825-832 [本文引用:2]
[28]	S. G. Kim, W. T. Kim, T. Suzuki Phys. Rev. E, 60(1999), pp. 7186-7197 [本文引用:4]
[29]	B. Echebarria, R. Folch, A. Karma, M. Plapp Phys. Rev. E, 70(2004) 061604 [本文引用:1]
[30]	T. Suzuki, M. Ode, S. G. Kim, W. T. Kim J. Cryst. Growth, 237(2002), pp. 125-131 [本文引用:1]
[31]	F. Luo, X. R. Chen, L. C. Cai, G. F. Ji J. Chem. Eng. Data, 55(2010), pp. 5149-5155 [本文引用:1]
[32]	W. J. Zhang, Y. F. Peng, Z. L. Liu Physica B, 440(2014), pp. 33-40 [本文引用:1]
[33]	N. Saunders, A. P. Miodownik Calphad: A Comprehensive Guide Pergamon, Oxford(1998), p. 91 [本文引用:2]
[34]	N. Saunders CALPHAD, 14(1990), pp. 61-70 [本文引用:1]
[35]	E. Brosh, G. Makov, R. Z. Shneck CALPHAD, 31(2007), pp. 173-185 [本文引用:1]
[36]	E. Brosh, R. Z. Shneck, G. Makov J. Phys. Chem. Solids, 69(2008), pp. 1912-1922 [本文引用:3]
[37]	R. Xu Mater. Lett, 59(2005), pp. 2818-2820 [本文引用:1]
[38]	H. L. Lukas, S. G. Fries, B. Sundman Computational Thermodynamics: The Calphad Method Cambridge University Press, Cambridge(2007), p. 34 [本文引用:1]
[39]	R. S. Qin, E. R. Wallach Acta Mater, 51(2003), pp. 6199-6210 [本文引用:1]
[40]	Z. Q. Han, H. W. Pan, Y. D. Li, A. A. Luo, A. K. Sachdev Metall. Mater. Trans. B, 46(2015), pp. 328-336 [本文引用:1]
[41]	E. Fraś, K. Wiencek, M. Górny, H. F. López, E. Olejnik Metall. Mater. Trans. A, 44(2013), pp. 5788-5795 [本文引用:1]

0.0

... Squeeze casting diminishes this defect, which expands the usage of Mg-Al alloy due to the higher integrity and better mechanical properties of products^[1] ...

0.0

... As metal is solidified under pressure in squeeze casting, pressure is essential for the nucleation^[2] and growth process^[3] of microstructure evolution, which exerts influence on the mechanical properties ...

... ^[2] studied the effect of pressure on the nucleation rate of Al alloy A356 and showed that for an industrial squeeze casting process with the applied pressure in the range from 80 to 100 MPa, increasing the applied pressure significantly increases the nucleation rate ...

0.0

... In the pressure range of several GPa, the phase diagrams of alloys are significantly changed, which exerts a great influence on solidification^[4] ...

0.0

... The superhigh pressure increases the nucleation density and decreases the solute diffusion coefficient, resulting in fine microstructure^[5] and high solid solubility^[6,7] ...

0.0

... The superhigh pressure increases the nucleation density and decreases the solute diffusion coefficient, resulting in fine microstructure^[5] and high solid solubility^[6,7] ...

0.0

... The superhigh pressure increases the nucleation density and decreases the solute diffusion coefficient, resulting in fine microstructure^[5] and high solid solubility^[6,7] ...

0.0

... In the pressure range of squeeze casting, more focus has been put on the enhancement of heat transfer between the casting and the mold due to the applied pressure^[8,9,10] ...

0.0

... In the pressure range of squeeze casting, more focus has been put on the enhancement of heat transfer between the casting and the mold due to the applied pressure^[8,9,10] ...

0.0

... In the pressure range of squeeze casting, more focus has been put on the enhancement of heat transfer between the casting and the mold due to the applied pressure^[8,9,10] ...

0.0

... The pressure reduces the air gap between the casting and the mold during solidification, which increases the cooling rate and results in the refinement of grain size^[11] ...

0.0

... The influence of process parameters on microstructure and mechanical properties has also been studied^[12] ...

0.0

... To better understand the microstructure evolution process, numerical modeling and simulation methods such as cellular automaton and phase field have been applied to investigate into the dendritic growth during solidification^[13,14,15] ...

0.0

2009

0.0

... developed a cellular automaton model with two sets of mesh to simulate equiaxed grain growth and columnar grain growth in directional solidification of Mg-Al alloy^[16,17,18] ...

0.0

... developed a cellular automaton model with two sets of mesh to simulate equiaxed grain growth and columnar grain growth in directional solidification of Mg-Al alloy^[16,17,18] ...

0.0

... developed a cellular automaton model with two sets of mesh to simulate equiaxed grain growth and columnar grain growth in directional solidification of Mg-Al alloy^[16,17,18] ...

0.0

... ^[19,20] conducted simulation of equiaxed solidification of Mg-Al alloy based on phase field method ...

0.0

... ^[19,20] conducted simulation of equiaxed solidification of Mg-Al alloy based on phase field method ...

0.0

... ^[21] simulated microstructure and micro segregation under pressure using cellular automaton method, in which the pressure was applied in only one direction, which is not comparable with real condition ...

0.0

... ^[22,23] investigated the effects of time-periodic external forcing on dendritic growth of CCH₃, a kind of liquid crystal, by experiments and phase field modeling, and found that the oscillating pressure and heating can tune the frequency of dendritic side-branching, indicating that thermal and mechanical effects are two dominant factors in interface stability ...

0.0

... For pressurized solidification, the pressure changes the solute diffusion condition and the free energy of various phases^[24], both of which impact the microstructure evolution ...

0.0

... Phase field models are thermodynamically consistent^[25] based on energy description of alloy systems, thus a phase field model taking the effect of pressure on solute diffusion and free energy of various phases into account is promising to simulate the microstructure evolution under pressure ...

0.0

... Phase field modelThe total free energy of the alloy system is defined as^[26] ...

... The interface region is defined as a mixture of solid and liquid with compositions different from each other, while restricted by the equal chemical potential condition based on KKS model^[26]: ...

0.0

... To develop a phase field model for multi-grain simulation, an orientational field is introduced into the model instead of adopting multi-phase field model^[27] ...

... The governing equations for the phase field, the orientational field and the concentration field are given as follows^[27]: ...

0.0

... Based on the one-dimension equilibrium solution, the parameters of the phase field can be given as follows^[28] ...

... 94^[28] ...

... is related to the interface kinetics, which is given as^[28] ...

... ^[28] and Qin and Wallach^[39], in the phase field simulation, the phase field driving force of the system is defined as ...

0.0

... ^[29], the interface width should be smaller than physical relevant length scale of the problem concerned, which in solidification is the tip radius for dendritic growth ...

0.0

... The anisotropy is introduced into the interface energy and the gradient energy coefficient, which is shown below^[30], ...

0.0

... ^[31] and Zhang et al ...

0.0

... ^[32] studied the effect of pressure on the interface energy of Ni and Co by using molecular dynamics, respectively ...

0.0

... Thermodynamics and Gibbs free energy under pressureThe Gibbs free energy for each phase of Mg-Al alloy can be described by Redlich-Kister equation as follows^[33]: ...

... The excess energy of mixing is given as follows^[33]: ...

0.0

... The parameters A and B are referred to the thermodynamic description of the Mg-Al system from Saunders^[34] ...

0.0

... The Gibbs free energy under pressure is calculated based on the quasi-harmonic approximation and equation of state (EOS)^[35] as follows: ...

0.0

... 1 suggested by Brosh^[36] is adopted, which takes the advantage that the isobaric heat capacity converges to the isochoric heat capacity at the limit of infinite pressure: ...

... ^[36] ...

... Effect of Gibbs free energy on dendritic growthBased on the model of Brosh^[36], the Gibbs free energy of solid and liquid phases of Mg-Al alloy under atmospheric and elevated pressures is depicted in Fig ...

0.0

... Solute diffusion coefficient under pressureAs the viscosity of the melt increases with the increase of pressure, based on the equation describing the effect of pressure on diffusion coefficient shown as follows, the solute diffusion coefficient is affected by the pressure significantly^[37] ...

0.0

... Solute partition coefficientThe common tangent of Gibbs free energy method^[38] is applied to calculate the equilibrium solute concentration and the partition coefficient of Mg-Al alloy in squeeze casting ...

0.0

... ^[28] and Qin and Wallach^[39], in the phase field simulation, the phase field driving force of the system is defined as ...

0.0

... and our previous experimental study on squeeze casting of AZ91 Mg alloy^[40], the dependence of nucleation rate of Mg-Al alloy on undercooling and pressure is calculated and shown in Fig ...

0.0

... To calculate the nucleation density in 2D simulation, Poisson-Voronoi model^[41] is adopted, which is shown as follows, where N_V is the nucleation density in three dimensional space and N_S is the nucleation density in two dimensional space ...