Tensile elastic behavior of bulk Zr46(Cu4.5/5.5Ag1/5.5)46Al8 metallic glass was experimentally investigated. It exhibited linear and non-linear time-independent elastic deformation with a demarcative stress of approximately 500 MPa within the timescale in the present work, and repeated loading–unloading before yielding did not alter stress–strain relationship. The pure linear elastic strain limit is 0.6%, significantly lower than 2% as generally reported, but still much higher than 0.1% observed for typical crystalline alloys. Deviation from linear elastic behavior at stresses higher than 500 MPa is explained here as a macroscopic manifestation of local fluctuations in elastic strain, which becomes pronounced at stresses higher than the critical value. The occurrence of non-linear elasticity is possibly also related to the sinusoidal relationship between shear stress and atomic displacement.
As possessing liquid-like atomic structure without long-range atomic periodicity, bulk metallic glasses (BMGs) have great potential to be utilized as functional and structural materials owing to high strength, unique nanoimprinting capacity, low elastic modulus, excellent corrosion and wear resistance, good magnetic property, and large elastic strain limit about 2% [1], [2], [3] and [4], even up to 6% elastic strain limit for nanometer-sized MG [5]. However, major drawback of BMGs is the catastrophic and instantaneous brittle failure in tension, which severely limits their application as structural materials [6], [7], [8] and [9]. If only pure elasticity is employed in the actual applications, the brittleness does not preclude the service of BMGs. In strain-sensing devices, for example, BMGs exhibit distinct advantages over conventional polycrystalline alloys in performance. A strain-sensing device generally transforms pressure/stress parameter into displacement. Therefore, signal linearity and strain magnitude are two key factors influencing measurement accuracy, sensitivity and range. In order to have a better measurement performance, the material for the sensing element is required to possess high strength, large elastic strain limit and low elastic modulus, which are exactly characteristics of BMG materials. Most conventional polycrystalline alloys have much lower elastic strain limits and higher elastic moduli than BMGs [10].
Elastic behavior of solids includes ideal elasticity (linear elasticity and non-linear elasticity) and viscoelasticity (or anelasticity) [11]. For better transferring linearity of the strain-sensing devices, much attention needs to be focused on the amount of linear elastic strain limit rather than the total elastic range. Elastic deformation of BMGs is generally considered to be linear [4], [12] and [13]. However, to the best of authors' knowledge, no dedicated studies on the elastic behavior of BMGs have been conducted. Questions like “what is the mode of elastic deformation for the BMGs” and “is the linear elastic limit strain of BMGs as large as 2%” are unsolved. The influence of repeated loading–unloading on subsequent elastic deformation behavior of BMGs is still required to be systematically investigated.
In the current investigation, we chose a model quaternary Zr–Cu–Ag–Al BMG to experimentally study the effect of incremental step loading and unloading on the elastic deformation behavior. Quaternary Zr46(Cu4.5/5.5Ag1/5.5)46Al8 (at.%) selected for this study has superior glass-forming ability (diameter at least 20 mm), and the prepared BMG specimen exhibits a high yield strength of about 1822 MPa under uniaxial compression [14]. Ingots of the Zr46(Cu4.5/5.5Ag1/5.5)46Al8 alloy were produced by arc-melting a mixture of raw elements with a purity level better than 99.9% in a Ti-gettered argon atmosphere. To ensure homogeneity, the master ingots were inverted and remelted several times, and subsequently suck-cast into water-cooled copper mold to form 1 mm thick plates with a width of 10 mm. Synchrotron radiation X-ray diffraction (SR-XRD) at BW5 station of HASYLAB, Hamburg and differential scanning calorimetry (DSC) measurements confirmed that the as-cast specimens were amorphous in nature.
The dog-bone shaped tensile specimen had a gauge section of 18.0 mm long by 2.0 mm wide by 1.0 mm thick. Tensile experiments were conducted using a uniaxial servo-hydraulic Instron machine in ambient condition. The strain within the gauge section of the specimen was measured by a clip-on extensometer with a sensitivity of 0.001% fully covering the gauge length, and the gauge factor defined as the ratio of fractional change in electrical resistance to the fractional change in length (strain) is about 2.
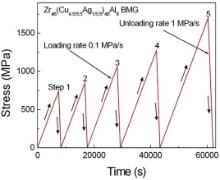
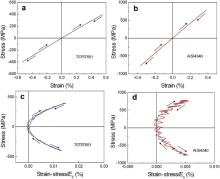
The test scheme for the incremental step loading and unloading for Zr46(Cu4.5/5.5Ag1/5.5)46Al8 BMG is shown in Fig. 1. The loading rate was 0.1 MPa/s and the unloading rate was 1 MPa/s. There were a total of five loading steps in the test and the maximum stress in each step ranged from 745 MPa to 1702 MPa as shown in Fig. 1, which is lower than apparent yielding stress under uniaxial compression in Ref.[14]. Fig. 2(a) shows the stress–strain curves obtained from Zr46(Cu4.5/5.5Ag1/5.5)46Al8 BMG with the five loading–unloading steps. It is clear that all the stress–strain curves for the five loading steps seem completely coincide and repeated loading–unloading does not alter the stress–strain relationship. This suggests the occurrence of recoverable and elastic deformation within the stress range up to 1702 MPa. In order to further elucidate the mode of elastic deformation, curves of stress–(strain–stress/ E0) are also shown in Fig. 2(b–f) for the five loading steps, respectively, where E0 (=93 GPa) is elastic modulus of the material determined from the initial loading stage. The value of E0 is consistent with the value derived from previous ultrasonic and density measurements [14]. The curve of stress–(strain–stress/ E0) consists of two parts: a vertically linear part and a non-linear part when the stress is larger than 500 MPa. The vertical linear part of the curve represents the linear elasticity of the stress–strain relationship. It appears that all the linear parts in the stress–(strain–stress/ E0) curves generated by the five loading steps have an identical upper range of 500 MPa. Therefore, the linear elastic limit of the material is 500 MPa and the corresponding elastic strain is approximately 0.6%. For each loading–unloading step, the loading and unloading curves coincided, and the strain completely returned to zero at the end of unloading. The stress–(strain–stress/ E0) curves were completely repeatable within the loading range tested. The tensile modulus of elasticity for Zr46(Cu4.5/5.5Ag1/5.5)46Al8 BMG keeps almost unchanged below 500 MPa, and it gradually decreases when the stress is increased from 500 MPa to 1702 MPa. These observations indicate that the stress–strain relationship of Zr46(Cu4.5/5.5Ag1/5.5)46Al8 BMG is linear elastic below 500 MPa, and becomes non-linear and time-independent in the stress range from 500 MPa to 1702 MPa within the timescale of the present study. It is the fact that we did not observe any time-dependent elastic deformation. Recent work [15], [16], [17], [18] and [19] on elastostatic loading of Ni–Nb and Cu–Zr binary metallic glasses shows that if the loading time is sufficient, homogeneous flow can be induced at room temperature accompanied by the changes in stored heat of relaxation (free volume) and compressive plasticity. A detectable anelastic deformation was also detected in Zr46.75Ti8.25Cu7.5Ni10Be27.5 BMG [20] at room temperature with the load close to the yield stress. Due to different loading and unloading rates adopted in this work, the anelastic component of deformation may be detected, if it exists. From the experimental results mentioned above, it can be concluded that the time-dependent elastic deformation (anelasticity) is indeed not detected in Zr46(Cu4.5/5.5Ag1/5.5)46Al8 BMG under tension. It may be related to the fact that the total holding time at the stress close to the yield strength is not as long as that adopted in Refs.[15–20] enough to induce anelasticity and plasticity. Deeper investigation concerning this phenomenon is still required.
Stainless steel has been traditionally used for conventional polycrystalline strain-sensing devices [21]. As a comparison, here we selected AISI4340 steel and 7075T651 aluminum alloy with different elastic moduli as representatives of conventional polycrystalline alloys. Fig. 3 shows the stress–strain curves obtained from testing AISI4340 steel and 7075T651 aluminum alloy under fully reversed tension–compression. The stress–(strain–stress/ E0) curves are also represented in Fig. 3, where E0 is elastic modulus of the material. The values of E0 were measured to be about 208 GPa and 73 GPa, respectively, for AISI4340 and 7075T651 alloys. It is evident in Fig. 3 that the loading and unloading paths are completely coincident during the tension–compression test for both materials within the loading ranges. Similar to the Zr-based BMG, the stress–strain curves of the two polycrystalline materials also display linear and non-linear elastic regions. The linear elastic limit is approximately 80 MPa and 200 MPa for 7075T651 aluminum alloy and AISI4340 steel, respectively. These linear elastic limits correspond to a strain of about 0.1%, which is much lower than 0.6% obtained for the BMG under the current investigation.
If slip is assumed to occur by sliding of one plane of atoms over another in a perfect crystal lattice, it is possible to estimate the shear stress required for such a movement, as illustrated in Fig. 4. As a rough approximation, the relationship between shear stress and atomic shear displacement can be expressed by a sine function τ = τ0sin(2π x/ b) [11], where τ0 is the amplitude of the sine wave or the theoretical shear strength, b is the distance between atoms in the slip direction, x is the displacement in the slip direction between the pair of adjacent lattice planes. In a real crystalline material, the existence of crystal defects responsible for plastic deformation significantly reduces the shear strength of the material, for example, the theoretical shear strength of metal crystal is at least 100 times greater than the observed shear strength [22], but the relation between shear stress and displacement still holds. It is evident from Fig. 4 that before the material begins to yield, the required shear stress does not linearly increase with the atomic shear displacement, i.e. the increase rate of shear stress gradually reduces. This is consistent with the observed experimental results of non-linear elasticity in AISI4340 and 7075T651 alloys. Schuh et al. [23] have revealed that in MGs the curve of shear stress vs atomic displacement is very similar to that of crystalline materials shown in Fig. 4. The difference is that the applied pressure/stress plays an important role in affecting the maximum value of shear stress, i.e. compressive stress increases it while tensile stress decreases it, because the Mohr–Coulomb criterion taking into account the effect of normal stress on shear plane can preferably describe deformation behavior of amorphous alloys by computer simulation and experimental analysis rather than the von Mises and Tresca criteria considering only shear stress [4], [24] and [25]. Therefore, the non-linear elasticity in MGs may be also associated with the sinusoidal correlation of shear stress and displacement.
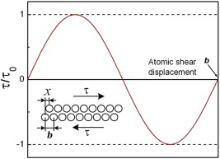 | Fig. 4. Schematic diagram of variation of shear stress with atomic shear displacement in slip direction in a perfect crystal lattice. |
The elastic behavior of a material is a macroscopic manifestation of atomic bonding, and elastic modulus reflects the bond strength. In a previous work, we examined the change of local atomic elastic strain for several BMGs with increasing tensile stress by SR-XRD [26]. It was found that the heterogeneity of local atomic elastic strain became distinct as the tensile stress was increased. For instance, the local atomic elastic strain is relatively homogeneous at a stress level of about 500 MPa for Zr48Cu43Ag2Al7 BMG, but the fluctuation of local elastic strain evidently occurs above the critical stress, and the observed average local elastic strain is slightly less than the calculated theoretical strain. Since the composition and mechanical property of the Zr48Cu43Ag2Al7 BMG are very similar to those of the material in this work, it is not unreasonable to use the experimental results of Zr48Cu43Ag2Al7 BMG to explain the phenomenon observed here. With increasing tensile stress above the critical value about 500 MPa, the local atomic elastic strain becomes more and more heterogeneous, and such a strain fluctuation is caused by the local change in elastic modulus of the BMG. Meanwhile, the slight decrease in elastic modulus deduced from SR-XRD as the tensile stress is above the critical stress consists also with the deviation from the linearity in Fig. 2(b–f). In crystalline solids, only single-crystal whiskers with diameters in the order of micrometers can be deformed in a linear elastic way up to a strain ranging from about 0.6% to 2.0% [11] and [27] owing to the inexistence of structural defects. However, synthesis of large-sized whiskers without defects is very difficult and expensive. Evidently, BMGs possess an essential superiority over the conventional polycrystalline alloys as the materials of the strain-sensing devices owing to the characteristics of large linear elastic strain limit, high tensile strength and low elastic modulus.
In summary, experimental investigation of Zr46(Cu4.5/5.5Ag1/5.5)46Al8 BMG under repeated zero-tension loading revealed that the BMG exhibited linear and non-linear time-independent elastic deformation within the studied time period. The linear elastic limit was found to be about 500 MPa, and the corresponding linear elastic strain limit is approximately 0.6% which is much lower than the reported elastic strain of 2% for BMGs. As a comparison, the linear elastic strain limit for AISI4340 steel and 7075T651 aluminum alloy, two conventional polycrystalline alloys, is approximately 0.1%. Repeated elastic deformation history did not affect the stress–strain relationship of the BMG under investigation. Lower elastic modulus and higher value of stress at which the stress–strain curve starts to show non-linear behavior are favorable for BMGs to be used in strain-sensing devices. Deviation from linear behavior at stresses higher than 500 MPa is explained here as a macroscopic manifestation of local fluctuations in elastic strain, which becomes pronounced at stresses higher than a critical value. The non-linear elastic deformation in the BMG may be also associated with the sinusoidal relationship between shear stress and atomic shear displacement.
References
Financial supports from the National Key Basic Research Program of China (No. 2012CB825700), the National Natural Science Foundation of China (Nos. 50701038, 10979002, 51371157 and 11179026), the Natural Science Foundation of Zhejiang Province (Nos. Y4110192 and Z1110196), and the Fundamental Research Funds for the Central Universities (2014FZA4006) are gratefully acknowledged.
| 1. |
|
| 2. |
|
| 3. |
|
| 4. |
|
| 5. |
|
| 6. |
|
| 7. |
|
| 8. |
|
| 9. |
|
| 10. |
|
| 11. |
|
| 12. |
|
| 13. |
|
| 14. |
|
| 15. |
|
| 16. |
|
| 17. |
|
| 18. |
|
| 19. |
|
| 20. |
|
| 21. |
|
| 22. |
|
| 23. |
|
| 24. |
|
| 25. |
|
| 26. |
|
| 27. |
|