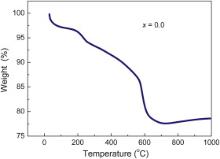
The samples by autocatalytic combustion process of the prepared sample were investigated by thermal gravimetric analysis (TGA). Fig. 1 shows the TGA result conducted on the powder of prepared samples for x = 0.0. From the analysis of TG data, three obvious mass losses were observed with a total weight loss of 23%. An extremely weak mass loss of around 3% is observed before 100 °C due to the evaporation of water vapours. In the second step of weight loss, the weight loss is around 10% ascribed to the decomposition of organic fuel/complexing agent and nitrates at 250–580 °C. In the third step, weight loss is found to be around 10% due to phase formation of the material at 580 °C because of decomposition of nitrates into oxides. A subsequent minor weight loss occurred after this range and then it became constant due to the phase formation. That means that the precursor generates a stable phase after the heat-treatment at higher than 600 °C. Also, from the TGA curve, it is seen that after 700 °C, there is a little increase in weight observed (∼1%) upto 1000 °C. This little increase might be due to the oxidation process involved at particular temperature ^[17]. Similar behaviour has been seen for x = 0.05.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Typical thermogram for Li0.5Ce xFe2.5- xO4.

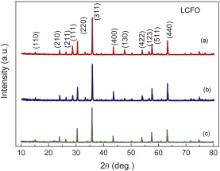
Fig. 2 illustrates the XRD patterns of the different compositions of the Li_0.5Ce _xFe_{2.5- x}O₄ sintered at 900 °C. The samples show all the characteristic reflections of ferrite material with the most intense (311) peak, which confirms the formation of cubic inverse spinel structure. The results obtained by XRD are indexed using JCPDS reference code 01-088-0671. The phase pure crystallites are formed in a stable cubic structure of space group p4332 and lattice parameter was found with a refinement from celref3 software. We have calculated quantities such as lattice parameters, unit cell volume of all the materials and these are provided in . It can be observed explicitly from XRD patterns that Ce is completely substituted into lithium ferrite for cerium concentration Ce = 0.05. But in the case of Ce = 0.1, the second phase of CeO₂ was also observed. The second phase peaks (111) and (123) appeared in Ce = 0.1 ^[12]. The lattice constant of Li_0.5Ce _xFe_{2.5- x}O₄ ( x = 0.05) is a = 0.83386 nm, which is slightly larger than that of Li_0.5Fe_2.5O₄ ( a = 0.83295 nm). This increase in lattice constant may be attributed to the replacement of smaller Fe³⁺ (0.0645 nm) ions by the larger Ce³⁺ (0.1034 nm) ions in the Li_0.5Ce _xFe_{2.5- x}O₄ system. This reveals that the doping by Ce does not change the cubic structure of Li_0.5Fe_2.5O₄, and Ce was substituted into the crystal lattice.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. XRD patterns of 900 °C Li0.5Ce xFe2.5- xO4 system: (a) x = 0.0, (b) x = 0.05, (c) x = 0.1.

Table 1.

Table 1.

Table 1. Cell parameters and density of two samples Li0.5Ce xFe2.5- xO4, where x = 0 and 0.05 Sample Activation energy from impedance (eV) Activation energy from modulus, EP (eV) (±0.05) Dc conduction, Eσ (±0.05) Cross over frequency, EP (±0.05) LCFO-0.0 0.64 0.60 0.59 LCFO-0.05 0.69 0.65 0.65

Table 1. Cell parameters and density of two samples Li0.5Ce xFe2.5- xO4, where x = 0 and 0.05

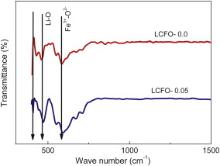
Fig. 3 shows the FTIF spectra of Li_0.5Ce _xFe_{2.5- x}O₄ system. The FTIR spectrum of pure lithium ferrite ( x = 0) indicates the presence of splitting in the absorption bands. The first primary band ( ν₁) at 592 cm ^-1 has a structure consisting of three subsidiary bands ν₁(1), ν₁(2), ν₁(3) at 709.8, 677 and 546 cm^-1, respectively. The second primary band ( ν₂), which should be at 400 cm^-1, is characterized by different splitting bands. It has been shown by Potakova et al. ^[18] that splitting is observed on absorption bands due to presence of Fe²⁺ ions in ferrites. The Fe²⁺–O^2- vibrations will come below 400 cm^-1 range. In other words, this band can be assigned to the divalent metal ion–oxygen complexes on octahedral sites, which cannot be shown here. The band at ν₂(1) = 470 cm^-1 and the weak one at ν₂(2) = 407 cm^-1 can be attributed to Li–O vibrations. The spectra of Li_0.5Ce _xFe_{2.5- x}O₄ system show a change and shift in the absorption bands when Ce³⁺ ions are introduced. For x = 0.05, there is no more shift in the band or intensity.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. FTIR spectra of Li0.5Ce xFe2.5- xO4 system for x = 0.0 and 0.05.

The density of sample bits with free of air bubbles and cracks upon visual examination, was determined by the Archimedes principle. The density of the samples under study was determined by using specific gravity bottle, Shimadzu single pan balance for weight measurements and xylene as the inert liquid. Density was obtained by employing the relation: ρ = W_a ρ_l/( W_a - W_l), where ρ is the density of the sample, W_a is the weight of the sample in air, W_l is the weight of the sample when being fully immersed in liquid and ρ_l is the density of liquid used. The error in the density measurements is within ±(0.04) g/cm³. The calculated and measured densities of all the materials are given in .

3.5.1. Impedance studies

The parallel conductance G and capacitance C of the samples were measured at varies angular frequency ω = 2π f, f being the frequency. The real Z′( ω) and the imaginary Z″( ω) parts of the complex impedance Z^∗( ω) are calculated with measured G and C by using the relations:

Z^′(ω)=G/(G²+ω²C²) (2)

Z^″(ω)=Cω/(G²+ω²C²) (3)

Since the early days of Cole–Cole, considerable progress has been made in utilizing complex plane plots and frequency explicit plots to explain the electrical conductivity of a wide range of solid state materials. The equivalent circuit, which is modelled by the Cole–Cole function, is given by:

Z*=R/[1+(jωτ)^1-α] (4)

where τ= RC and 0 ≤ α<1 characterizes the distribution of the relaxation times and for an ideal Debye relaxation α= 0.

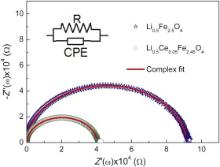
Fig. 4 shows the complex impedance plot for Li_0.5Fe_2.5O₄ (LCFO-0.0) and Li_0.5Ce_0.05Fe_2.45O₄ (LCFO-0.05) at 280 °C and the solid lines are the best fit to Eq. . The curves start at the origin, and hence there is no need of resistance in series to model the sample. The shape of the curve suggests that the electrical response is completely dominated by the bulk properties of the material. As per the plots, the semicircles have their centres located slightly away from the real axis, which indicates departure from ideal Debye behaviour ^[19]. It is seen that the semicircular arcs are shifted towards the origin, indicating the increase in conductivity of all samples as the temperature increases. As temperature increases, the radius of the arc corresponding to bulk resistance of the material decreases, which indicates an activated conduction mechanism. The results suggest that the non-Debye model is suitable for representing the samples and the impedance data are fitted by the resistance–constant phase elements (R–CPE) circuit ^[20].

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Complex impedance spectra of Li0.5Ce xFe2.5- xO4 system at 280 °C.

AC impedance data are explained based on the well known concept of CPE and is given by:

ZCPE=1/(Y0n(iω)) (5)

where 0 ≤ n≤ 1. When n= 0, Y₀becomes 1/ R and CPE behaves as a pure resistor and for n= 1, Y₀becomes C and CPE behaves as a pure capacitor with reactance value 1/( Cω). If the value of nis between 0 and 1, CPE takes the value of neither the capacitance nor the resistance; but it is a combination of resistance and capacitance. The CPE is used to describe (a) distribution of the value of some physical property of the system and (b) microscopic (non-Debye) process. The electrical properties of an ion conductor can be described by an equivalent circuit consisting of a parallel combination of a resistor Rand a capacitor C. The complex impedance diagram of such a circuit gives a semicircle, centred on the Z′ axis at ( R/2, 0). However, in most cases the experimental data reveal a significant deviation from simple R– Cbehaviour, and it is apparent in terms of depressed semicircle in complex impedance. A common phenomenological approach describes these broadened/dispersed semicircles by a parallel connection of an Ohmic resistor Rand a constant phase element (CPE). In Fig. 4, the bulk property is represented by the equivalent circuit (R–CPE), where Rand CPE are parallel and CPE accounts for depressed semicircle. The elements of an equivalent circuit model represent various (macroscopic) processes involved in transport of mass and charge. A more general non-linear least square (NLLS) fit program based on Levenberg–Marquardt algorithm has been used to extract the impedance parameters using Origin 8 software. The magnitudes of Rand CPE at 553 K are given infor different compositions. On separating real and imaginary parts of Eq.we obtained:

$Z^{\prime }=\frac{R\left(1+{\left(\omega \tau \right)}^{\left(1-\alpha \right)}\cos \left[\left(1-\alpha \right)\text{π}/2\right]\right)}{1+{\left(\omega \tau \right)}^{2\left(1-\alpha \right)}+2{\left(\tau \omega \right)}^{1-\alpha }\cos \left[\left(1-\alpha \right)\text{π}/2\right]}$ (6)

$Z^{″}=\frac{R{\left(\omega \tau \right)}^{1-\alpha }\sin \left[\left(1-\alpha \right)\text{π}/2\right]}{1+{\left(\omega \tau \right)}^{2\left(1-\alpha \right)}+2{\left(\tau \omega \right)}^{1-\alpha }\cos \left[\left(1-\alpha \right)\text{π}/2\right]}$ (7)

Table 2.

Table 2.

Table 2. Equivalent circuit and the parameter values for different compositions at 553 K Sample Temperatures (K) Equivalent circuit Parameter values LCFO-0.0 553 R–CPE R = 9.15 × 104 ± 33.00 CPE = 2.13 × 10-10 ± 4.37 × 10-13 n = 0.97 ± 6.7 × 10-4 LCFO-0.05 553 R–CPE R = 4.07 × 104 ± 30.00 CPE = 2.22 × 10-10 ± 2.10 × 10-13 n = 0.96 ± 4.9 × 10-4

Table 2. Equivalent circuit and the parameter values for different compositions at 553 K

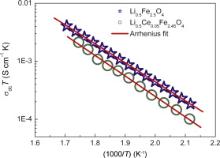
Fig. 5(a) and (b) shows plots between Z″ vs ω at various temperatures for the prepared ferrites. The peak that is exhibited by Z″ shifts towards higher frequencies with the increase in temperature. The curves are broader than ideal Debye curve and asymmetric. These features indicate that the relaxation time τ is not single valued but it is the average value of distribution of relaxation time τ_m = 1/ ω_p, where ω_p is the peak frequency ^[19]. As temperature increases, the magnitude of Z″ peak maxima decreases and the peak frequency shifts to the higher temperature values ^[21]. Solids lines in Fig. 6(a) and (b) are the fitted curves to the experimental results according to Eq. . It is clear that the experimental data are closely fitted using Eq. in the entire range of frequencies. The dc conductivity is obtained by using the formula: σ_dc = L/ RA, where L is thickness and A is area of cross section of the sample. Generally conductivity in this kind of material follows Arrhenius relation as

σ_dcT= σ₀exp(-E_σ/k_B) (8)

where σ_dc is the dc conductivity, σ₀ is the pre-exponential factor, T is the temperature in K, E_σ is the dc conductivity activation energy and k_B is the Boltzmann's constant. The Arrhenius plot for temperature dependence of dc conductivity of different compositions is shown in Fig. 6. The activation energy for the conduction process is calculated from the slope, which is given in. The insets of Fig. 6(a) and (b) show dependence of relaxation time on the reciprocal temperature. It was also found that the reciprocal temperature dependence of hopping frequency, ω_Pshows Arrhenius behaviour as

ω_P=ω_oexp(-E_P/k_BT) (9)

where ω_o is pre-factor, E_P is activation energy for relaxation. The solid lines in the inset of Fig. 6(a) and (b) figures are the linear fit to experimental data according to Eq.. The activation energy calculated for hopping frequency is found to be almost same with the activation energy calculated from conductivity, which is shown in.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Variation of imaginary part of impedance Z″ with frequency at different temperatures for: (a) LCFO-0.0, (b) LCFO-0.05, Inset: activation energy plot for hopping frequency.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Arrhenius plot of ( σdc T) vs reciprocal of temperature.

Table 3.

Table 3.

Table 3. Activation energies obtained from Arrhenius plots and dc conductivity values from different representations Sample Unit cell parameter (nm) Unit cell volume, Vm (cm3) Molecular weight, M (g) Calculated density (g/cm3) (±0.04) Measured density (g/cm3) (±0.04) LCFO-0.0 0.83295 577.91 207.08 4.75 4.15 LCFO-0.05 0.83386 579.82 211.29 4.84 4.20

Table 3. Activation energies obtained from Arrhenius plots and dc conductivity values from different representations

From the experimental data it has been seen that, the activation energy increases with the increase of cerium proportion. The increase in activation energy may be explained in terms of ionic radii of Ce³⁺ and Fe³⁺. The larger Ce³⁺ (0.1034 nm) ions substitution in octahedral B site having smaller Fe³⁺ (0.0645 nm) ions in the Li_0.5Ce _xFe_{2.5- x}O₄ system. The ionic radius of the Ce³⁺ is almost twice that of Fe³⁺ ionic radius and it may causes the oxygen (O^2-) anion distortion. The distorted anion may trap the Li⁺ and it needs more energy to conduct. This could be the reason to increase the activation energy in the Ce doped lithium ferrite ^[22].

3.5.2. Electric modulus

An alternative approach to investigate the electrical response of materials is given by complex electric modulus M^∗( ω)

M*(ω)=M^′(ω)+jM^″(ω) (10)

where M′( ω) and M″( ω) are real and imaginary, respectively and they are given by:

M^′(ω)=ωɛ0AZ^″(ω)/L (11)

M^″(ω)=ωɛ0AZ^′(ω)/L (12)

where L is thickness and A is area of cross section of the sample. Electric modulus representation M^*( ω) = 1/ ɛ^*( ω) was developed by Provenzano et al. ^[23] and it is one of the methods to understand the electrical relaxation process of hopping charge carriers in ion/electron conducting materials, where the low frequency electrode polarization effects are suppressed ^[24].

The dielectric relaxation process, in general, can be represented by the numerical Laplace transform of Kohlraush–Williams–Watts (KWW) decay function φ( t) = exp[-( t/ τ) ^β], where the exponent β characterizes the degree of non-Debye behaviour and τ is the conductivity relaxation time as:

$M^{\text{*}}\left(\omega \right)=M_{\infty }\left[1-{\int }_0^{\infty }{\text{e}}^{-j\omega t}\left\{\frac{*\phi }{*t}\right\}*t\right]=M_{\infty }[1-N^{*}\left(\omega \right)]$ (13)

where

$N^{\text{*}}\left(\omega \right)=1-{\int }_0^{\infty }{\text{e}}^{-j\omega t}\left\{\frac{*\phi }{*t}\right\}*t$

and M_∞= 1/ ɛ_∞ is the inverse of the high-frequency dielectric permittivity and the function φ( t) is the time evolution of the electric field within the dielectric, the exponent β characterizes the degree of non-Debye behaviour and is related to the full width at half maximum of M″( ω) vs ω curve.

Later on Bergman ^[25] modified the KWW function fitting approach, allowing direct analysis in the frequency domain. In the frequency domain the imaginary part of the M″( ω) has been approximated as (for β ≥ 0.4)

$M^{″}\left(\omega \right)=\frac{M_{\max }^{″}}{1-\beta +\frac{\beta }{1+\beta }{\left[\beta \left({\omega }_{\max }/\omega \right)+\left(\omega /{\omega }_{\max }\right)\right]}^{\beta }}$ (14)

Where $M_{\max }^{″}$ is the peak maximum of the imaginary part of the modulus and ω_max= 1/ τ, ( τ is the conductivity relaxation time) is the peak frequency of the imaginary part of the modulus. Fig. 7(a) and (b) shows respectively the real parts and imaginary part of electric modulus as a function of frequency for Li_0.5Ce_0.05Fe_2.45O₄ at selected temperatures. In Fig. 7(a) at all temperatures M′( ω) reaches a constant value at high frequencies and tends to zero at low frequencies suggesting negligible or absence of electrode polarization.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Variation of real (a) and imaginary (b) part of electric modulus with frequency for LFCO-0.05 respectively at different temperatures.

The M″( ω) shows a slight asymmetric peak at each temperature as seen in Fig. 7(b). The low frequency wing of the peak represents the range of frequencies, in which the charge carriers can move over long distances, i.e. they can perform successful hopping from one site to the neighbouring site. On the other hand, corresponding to the high-frequency wing of the M″( ω) peak, the charge carriers are spatially confined to their potential wells and the charge carriers can make only localized motion within the well. The peak is positioned at around the centre of the dispersion. The peak frequency shifts towards higher frequencies with temperature. The M″( ω) is related to the energy dissipation taking place in the irreversible conduction process. This is due to the reason that the dielectric relaxation observed in these systems does not correspond to a single relaxation time function. Similar behaviour has been seen for Li_0.5Fe_2.5O₄ sample. The peak maximum M_max, peak frequency ω_max = 1/ τ and stretching exponent β are obtained from M″( ω) data by using Eq. for the materials and typical fitted curves are shown in Fig. 8.

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. Arrhenius plot of ωmax for the compositions from electric modulus.

Cross over frequency from conductivity relaxation time τ = 1/ ω_max obtained from Bergman fitting approach for x = 0.0 and 0.05 materials is plotted as a function of reciprocal temperature 1000/ T in Fig. 8. The ω_max = 1/ τ is temperature dependent and is found to obey the Arrhenius equation given in Eq.(9). The activation energy E_P has been obtained as shown in Table 2.

For both the samples, the imaginary part of modulus M″ has been scaled by $M_{\max }^{″}$ and each frequency by ω_max at different temperatures according to the formalism ^{[26], [27] and [28]}:

$M^{″}\left(\omega \right)/M_{\text{max}}^{″}=F\left(\omega /{\omega }_{\text{max}}\right)$ (15)

where symbols have their usual meaning. The nearly overlapping nature of the data for all temperatures into a single master curve indicates the same thermal activation energy at different frequencies ^{[29], [30] and [31]}and the dynamical process is temperature independent, which is shown in Fig. 9(a) and (b).

Fig. 9.

	Figure Option ViewDownloadNew Window
	Fig. 9. Scaled modulus plots for (a) LCFO-0.0 and (b) LCFO-0.05, where modulus axis M″( ω) is scaled by $M_{\max }^{″}$ the peak of M″( ω) and frequency axis ω by ωmax.

Similarly, each imaginary part of impedance data is scaled by $Z_{\max }^{″}$ and each frequency is scaled by ω_p at different temperatures according to the formalism:

$Z^{″}\left(\omega \right)/Z_{\text{max}}^{″}=F\left(\omega /{\omega }_{\text{P}}\right)$ (16)

where symbols have their usual meaning. These results are shown in Fig. 10(a) and (b). Here the scaled impedance spectra collapsed into a single master curve. The ability to scale different data sets so as to collapse to a master curve indicates that the process can be separated into a common physical mechanism modified only by thermodynamic scales. This master curve gives the dimensionless impedance and modulus as a function of dimensionless frequency ^{[32] and [33]}. The existence of such a master curve is referred to as time temperature superposition principle.

Fig. 10.

	Figure Option ViewDownloadNew Window
	Fig. 10. Scaling plots for the impedance spectra of LCFO-0.0 (a) and LCFO-0.05 (b), where the impedance and frequency axis are scaled by the maximum peak impedance and hopping frequency respectively.