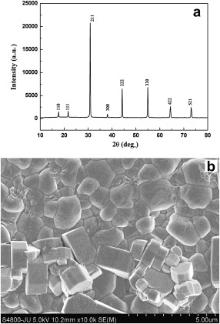
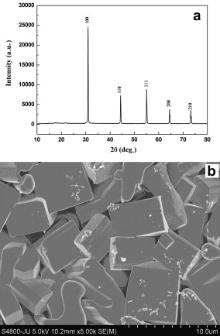
The PXRD patterns of the BMT and BZT are shown in Figs. 1(a) and 2(a), respectively. The PXRD patterns are indexed by the Rietveld based program NTREOR of EXPO2009 package. No unaccounted diffraction peak has been noted in the PXRD patterns of the samples (Figs. 1(a) and 2(a)). The analysis of PXRD pattern suggests that samples are in single phase and they have crystallized in cubic structure, with lattice parameter a = 0.708 nm for BMT and 0.451 nm for BZT. However according to previous reports, BMT is a hexagonal system having lattice parameters a = 0.5782 nm and c = 0.7067 nm whereas BZT possesses cubic structure with lattice parameter a = 0.41 nm ^{[34], [35], [36] and [37]}. Thus the results of our PXRD study for BZT corroborate with previous results ^{[36] and [37]}, but for BMT, the result of present structural study totally disagrees with the result reported previously ^{[34] and [35]}.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. XRD pattern (a) and SEM image (b) of Ba(Mg1/3Ta2/3)O3.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. XRD pattern (a) and SEM image (b) of Ba(Zn1/3Ta2/3)O3.

The Goldschmidt's tolerance factor T_f of ABO₃ type oxides is given by the formula

$T_{\text{f}}=\frac{r_A+r_{\text{O}}}{\sqrt{2}\left(r_B>+r_{\text{O}}\right)}$ (1)

where r _A and r_O are the ionic radii of A site and O ions, respectively and r _B denotes the average radius of ions at B site ^[40]. It may be noted that T_f is ≈1 for cubic perovskites, while for monoclinic or orthorhombic structures, T_f is usually <1 ^{[33], [40], [41] and [42]}. The values of T_f for BMT and BZT are 1.029 and 1.026, respectively, and the closeness of these values of T_f to 1 indicates that both BMT and BZT are cubic perovskite. Thus, the T_f values of the samples strongly support the results obtained by PXRD profile fitting and discard the previous reports on the structural studies of BMT.

The FESEM micrographs of BMT and BZT are presented in the Figs. 1(b) and 2(b), respectively. In the FESEM images, the samples displayed well-defined grains. The grain size is in the range of 0.28–1.76 μm and 1.39–6.67 μm for BMT and BZT, respectively. The grains of BMT and BZT are non-uniform in size. The grains of BMT have irregular shape, whereas the grains of BZT are rectangular in shape.

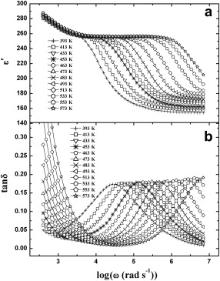
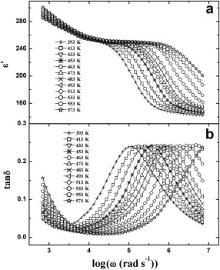
The logarithmic angular frequency ( ω = 2π υ) dependence of the real part ( ɛ′) of complex dielectric permittivity ( ɛ*) and loss tangent (tan δ) of the samples at some selective temperatures between 393 and 573 K have been depicted in Figs. 3 and 4. The plateaus in the ɛ′ vs log ω curves (Figs. 3(a) and 4(a)) move towards the higher frequency with increasing temperature. The nature of the ɛ′ vs log ω curves for the samples can be elucidated by Debye theory ^[43]. According to Figs. 3(a) and 4(a): (i) at low frequencies (where ω <<1/ τ, τ is the relaxation time), ɛ′ is almost constant, i.e., ɛ′ ≈ ɛ_s (the value of the dielectric constant at quasistatic field), so in low frequency range, the dipoles follow the electric field; (ii) in the frequency range where ω <1/ τ, the ɛ′ decreases slightly which implies that in this frequency range dipoles in the samples begin to lag behind the field; (iii) ɛ′ drops very sharply at the characteristic frequency where ω = 1/ τ. Thus our results strongly support the Debye theory of dielectric permittivity ^[43].

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Frequency dependence of ɛ′ (a) and tan δ (b) of Ba(Mg1/3Ta2/3)O3 at various temperatures.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Frequency dependence of ɛ′ (a) and tan δ (b) of Ba(Zn1/3Ta2/3)O3 at various temperatures.

Here, ɛ′ decreases sharply at higher frequencies. It is well known that the rate of polarization formed and the frequency of applied electric field control the dielectric relaxation process. Thus, the sharp decrease in ɛ′ at higher frequencies is thought to be due to the decay in polarization at higher frequencies of the applied electric field. It may be noted that at a particular temperature for a given frequency the values of ɛ′ for BMT and BZT are nearly equal. The reported value of ɛ′ of BNT is greater than that obtained for BMT and BZT. It is noteworthy that the ionic radius are r_Zn ≈ r_Mg > r_Ni. This reveals that the ionic radii of B type cations (alkaline earth element/transition metal) of the sample have an influence on the value of dielectric permittivity of Ba( B′_1/3Ta_2/3)O₃ ( B′ = Ni, Mg and Zn) type oxides.

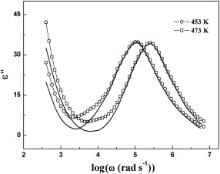
A peak in tan δ appears when the hopping frequency of the charge carriers is approximately equal to that of the externally applied field, i.e., when ω = 1/ τ. Now, in the present case, a well defined peak is observed in the tan δ vs log ω plots (Figs. 3(b) and 4(b)) of BMT and BZT and tan δ exhibits strong dispersions. These are indicative of the presence of dielectric relaxation in the samples. The peak in tan δ vs log ω curves for both the samples gets shifted towards higher frequency with increasing temperature as the polarization evolved at a high rate at higher temperatures. It is clearly evident from Figs. 3 and 4, the peak in tan δ is centered approximately at the characteristic frequency ( ω = 1/ τ) obtained from the ɛ′ vs log ω curves. This indicates that there is a strong correlation between dielectric behavior and the conduction mechanism of the samples as ɛ′ accounts for the dielectric property while tan δ is connected with the conduction loss. We have adopted the conductivity and electric modulus formalisms to study the relaxation mechanism of BMT and BZT.

Figs. 5(a) and 6(a) show the frequency dependence of ac conductivity for BMT and BZT at different measuring temperatures, respectively. The real part of ac conductivity ( σ) is given by σ( ω) = ɛ₀ ωɛ″. Two distinct plateaus are observed in the Figs. 5(a) and 6(a). The low frequency plateau represents the total conductivity whereas the high frequency plateau represents the contribution of grains to the total conductivity ^[26]. The presence of both the high and low frequency plateaus in conductivity spectra suggests that the two processes are contributing to the bulk conduction behavior. The total conductivity at a given temperature can be expressed by the power law of frequency,

σ(ω)=σdc+Aωn (2)

where σ_dc is the dc conductivity (the value of conductivity at the lowest frequency is taken as the dc conductivity of the samples) and A depends both on temperature and frequency.

Fig. 5.

	Figure Option ViewDownloadNew Window
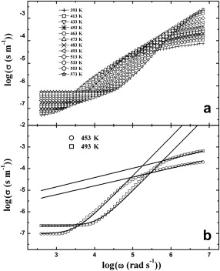	Fig. 5. (a) Frequency dependence of the conductivity ( σ) for Ba(Mg1/3Ta2/3)O3 at various temperature, (b) fittings of power law for the same at 453 and 493 K shown by solid lines.

Fig. 6.

	Figure Option ViewDownloadNew Window
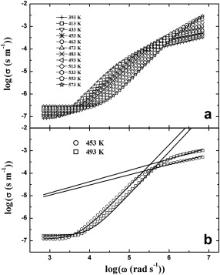	Fig. 6. (a) Frequency dependence of the conductivity ( σ) for Ba(Zn1/3Ta2/3)O3 at various temperature, (b) fittings of power law for the same at 453 and 493 K shown by solid lines.

In order to account for the two plateaus, the conductivity spectra are fitted by a pair of power law equations at two selected temperatures and are presented in Figs. 5(b) and 6(b). The basic power law used for this purpose is given by Eq. . The exponent n in the lower frequency region is found in the range of 1.5–1.9 and increases with increasing temperature ^[27]. In the high frequency region, the values of n are found to be in 0.4–0.6 ^[44]. The estimated fitting parameters are listed in . The low and high frequency regions represent the non-diffusing and localized diffusing modes, respectively. Based on this proposition, Ishii et al. ^[45] showed that the exponent n is greater than 1 and tends to attain 2 with increasing temperature in lower frequency region whereas it is less than 1 in the higher frequency region. Our results strongly corroborate this theory.

Table 1.

Table 1.

Table 1. Various fitted parameters of the conductivity spectra Materials Temperature (K) σdc (S m-1) A n BMT 453 (at low frequency) 0.96 × 10-7 0.48 × 10-13 1.798 BMT 453 (at high frequency) 0.96 × 10-7 3.59 × 10-7 0.410 BMT 493 (at low frequency) 2.27 × 10-7 0.48 × 10-13 1.798 BMT 493 (at high frequency) 2.27 × 10-7 6.89 × 10-7 0.435 BZT 453 (at low frequency) 1.20 × 10-7 0.21 × 10-13 1.825 BZT 453 (at high frequency) 1.20 × 10-7 4.55 × 10-7 0.454 BZT 493 (at low frequency) 1.69 × 10-7 0.05 × 10-13 1.879 BZT 493 (at high frequency) 1.69 × 10-7 4.06 × 10-7 0.503 Notes: σdc—dc conductivity (consider at lowest frequency), A and n are constants which depend on temperature and frequency.

Table 1. Various fitted parameters of the conductivity spectra

The electric modulus formalism offers the best opportunity to analyze the relaxation properties of polycrystalline ceramics ^{[45] and [46]}. The electric modulus represents the relaxation of the electric field in the sample when the electric displacement remains constant. It can be used to monitor the electrical properties of the material and is a useful technique to investigate the influences of temperature and frequency on the relaxation processes. The electric modulus M*( ω) is defined by the relation ^[47]:

$M^{\ast }\left(\omega \right)=M_{\infty }\left[1-\underset{0}{\overset{\infty }{\int }}{\text{e}}^{-j\omega t}\left(\frac{d\Phi \left(t\right)}{dt}\right)dt\right]$ (3)

where the function Φ( t) gives the time evaluation of the electric field within the dielectric.

The angular frequencies of real ( M′) and imaginary ( M″) parts of the complex electrical modulus as a function of temperature for BMT and BZT are shown in Figs. 7 and 8, respectively. Distinct peaks have been observed in the M″ vs log ω plots for both the samples. These pronounced peaks for M″( ω) clearly indicate that the samples exhibit relaxation phenomena. The peaks in M″( ω) shift towards higher frequencies with increasing temperature, which indicates that the relaxation rate enhances as the temperature increases. The frequency region below peak maximum ( M″_m) determines the range in which the charge carriers are mobile at long distances. At frequencies above peak maximum the carriers are confined to potential wells, being mobile on short distances. There may be a slight amount of oxygen vacancy in the present samples as they are synthesized at high temperature of about 1623 K. If vacancies are created then the space available for dipole vibration gets elongated, which in turn facilitates the short-range hopping of the ions and gives rise to strong relaxation. This feature has been noticed in the M″ vs log ω curves of both the samples.

Fig. 7.

	Figure Option ViewDownloadNew Window
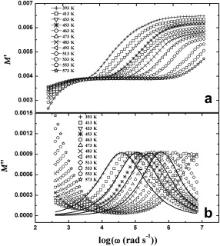	Fig. 7. Frequency dependence of M′ (a) and M″ (b) of Ba(Mg1/3Ta2/3)O3 at various temperatures where symbols are the experimental points and solid lines are the fitting to Eq. .

Fig. 8.

	Figure Option ViewDownloadNew Window
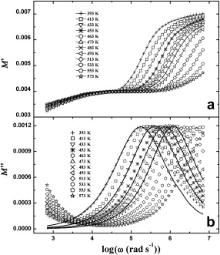	Fig. 8. Frequency dependence of M′ (a) and M″ (b) of Ba(Zn1/3Ta2/3)O3 at various temperatures where symbols are the experimental points and solid lines are the fitting to Eq. .

The large width of the loss peaks in tan δ vs log ω plots (Figs. 3(b) and 4(b)) suggests that the relaxation in the sample is polydispersive in nature. To account this effect we have considered a temperature dependent distribution function, g( τ, T) for relaxation time and expressed the imaginary part of complex dielectric permittivity as follows ^[26]:

${\varepsilon }^{″}=\varepsilon \left(0,T\right)\underset{0}{\overset{\infty }{\int }}g\left(\tau ,T\right)\frac{d\left(\omega \tau \right)}{1+{\omega }^2{\tau }^2}$ (4)

where ɛ(0, T) is the low frequency dielectric constant. In the limit of τ_min<1/ ω< τ_max, the real and imaginary parts of dielectric permittivity are connected by the simple relation ^{[48] and [49]}:

${\varepsilon }^{″}\left(\omega ,T\right)=\frac{\text{π}}{2}·\frac{\partial {\varepsilon }^{\prime }\left(\omega ,T\right)}{\partial \left(\ln \omega \right)}$ (5)

ɛ″ has been numerically calculated from the dispersion of ɛ′ by using Eq. and has been plotted against log ω along with the experimentally obtained values of ɛ″ (= ɛ′tan δ) at different logarithmic angular frequencies. The results are presented in Figs. 9 and 10 for BMT and BZT, respectively. A good matching between the experimentally obtained values of ɛ″ (= ɛ′tan δ) and those calculated by Eq. reveals that the spectrum g( τ, T) is broad in nature, i.e., samples exhibit polydispersive relaxation process. This could be further verified by Cole–Cole approach of electrical modulus formalism.

Fig. 9.

	Figure Option ViewDownloadNew Window
	Fig. 9. Comparison of measured ɛ″ vs log ω for Ba(Mg1/3Ta2/3)O3 with that calculated using Eq. at 453 and 473 K. The open symbols joined with line represent the experimental points and solid lines represent the ɛ″ calculated using Eq. .

Fig. 10.

	Figure Option ViewDownloadNew Window
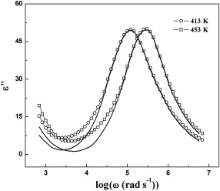	Fig. 10. Comparison of measured ɛ″ vs log ω for Ba(Zn1/3Ta2/3)O3 with that calculated using Eq. at 413 and 453 K. The open symbols joined with line represent the experimental points and solid lines represent the ɛ″ calculated using Eq. .

We already have shown that the relaxation exhibited by the samples is polydispersive in nature. To crosscheck our previous finding we have fitted the experimental electric modulus spectra of BMT and BZT with the Cole–Cole expression ^[50]:

$M^{″}=\frac{M_{\infty }{M}_{\text{s}}\left[\left(M_{\infty }-M_{\text{s}}\right)\sin \Phi \right]A}{M_{\text{s}}^2{A}^2+2A\left(M_{\infty }+M_{\text{s}}\right)M_{\text{s}}\cos \Phi +{\left(M_{\infty }-M_{\text{s}}\right)}^2}$ (6)

where

A=[1+2ωt1-αsin(απ/2)+ωt2(1-α)]^1/2 (7)

and

Φ=tan^-1{(ωt)^1-αcos(απ/2)/[1+(ωt)^1-αsin(απ/2)]} (8)

where M″ is the imaginary part of complex electric modulus. The polydispersive nature of the dielectric relaxation can be examined very easily by the Cole–Cole model. The Cole–Cole constant α will be positive but less than one (i.e., 0< α<1) when the dielectric relaxation in the sample is polydispersive in nature ^[51]. The solid lines in Figs. 7(b) and 8(b) represent the fitting of Cole–Cole functions. The estimated values of fitting parameters ( M_∞, M_sand α) at different temperatures are presented in. A very nice matching between the experimental and fitted results with 0< α<1 indicates that the relaxation in the samples is polydispersive in nature.

Table 2.

Table 2.

Table 2. Various Cole–Cole fitted parameters of the modulus formalism Materials Temperature (K) Ms M∞ α BMT 393 4.80 × 10-7 2.58 × 10-3 0.820 BMT 433 1.34 × 10-7 2.36 × 10-3 0.849 BMT 463 0.63 × 10-7 2.33 × 10-3 0.851 BMT 483 0.16 × 10-7 2.21 × 10-3 0.894 BZT 393 2.20 × 10-7 3.24 × 10-3 0.806 BZT 433 0.85 × 10-7 3.16 × 10-3 0.826 BZT 463 0.38 × 10-7 3.04 × 10-3 0.846 BZT 483 0.20 × 10-7 3.00 × 10-3 0.858 Notes: Ms—the value of M″ at the lowest frequency, M∞—the value of M″ at the highest frequency, α—constant in Cole–Cole function.

Table 2. Various Cole–Cole fitted parameters of the modulus formalism

The activation energy of BMT and BZT has been estimated from the temperature dependence of dc conductivity ( σ_dc), most probable relaxation frequency obtained from tan δ vs log ω plots and M″ vs log ω plots. The reciprocal temperature dependence of σ_dc (which is measured by four probe method) for BMT and BZT is shown in Fig. 11. The σ_dc of both the samples follows Arrhenius law, σdc=σ₀exp(-Eσ/(kbT)) with activation energy E _σ = 0.54 eV and 0.41 eV for BMT and BZT, respectively. Again the value of σ_dc for both the samples increases with increasing temperature. Thus the results of dc conductivity study clearly indicate that BMT and BZT exhibit semiconducting behavior.

Fig. 11.

	Figure Option ViewDownloadNew Window
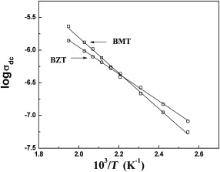	Fig. 11. Temperature dependence of dc conductivity for Ba(Mg1/3Ta2/3)O3 and Ba(Zn1/3Ta2/3)O3, respectively. Symbols are experimental points and solid lines are least squares straight-line fit.

A well defined peak has been obtained in the tan δ vs log ω plots and M″ vs log ω plots of all the samples at each of the measurement temperatures. The most probable relaxation frequency ( ω_m) can be obtained from the relation ω_m τ_m = 1, where τ_m is the most probable relaxation time. Fig. 12 depicts the log ω_m vs 10³/ T plots of BMT and BZT, where log ω_m has been determined from the peak position of loss tangent and electrical modulus spectra (Figs. 3(b), 4(b), 7(b) and 8(b)) of the respective samples. A numerical fitting of the log ω_m vs 10³/ T plots for BNT and BZT has been carried out ( Fig. 12) and it has been found that the most probable relaxation frequency follows the Arrhenius law:

${\omega }_{\text{m}}={\omega }_0\exp \left[\frac{-E_{\text{a}}}{K_{\text{B}}T}\right]$

where ω₀ is the pre-exponential factor and E_a is the activation energy of the corresponding process. The activation energies of BMT and BZT for tan δ are 0.54 and 0.40 eV, respectively and for M″ are 0.55 and 0.38 eV, respectively. These values match very well with the activation energies obtained from the Arrhenius plot of dc conductivity data. Thus, our results strongly suggest that all the samples are semiconducting in nature.

Fig. 12.

	Figure Option ViewDownloadNew Window
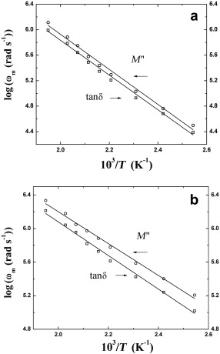	Fig. 12. Temperature dependence of the most probable relaxation frequency obtained from the frequency dependent plots of tan δ and M″ for Ba(Mg1/3Ta2/3)O3 (a) and Ba(Zn1/3Ta2/3)O3 (b), respectively. The symbols are the experimental points and the solid lines are the least squares straight-line fit.

We have scaled each ɛ″ by ɛ″_m and M″ by M″_m, where ɛ″_m and M″_m are the peak values of the imaginary part of dielectric permittivity and electrical modulus, respectively. Similarly, each frequency is scaled by ω_m ( ω_m corresponds to the frequencies of the peak positions of ɛ″ and M″ in the ɛ″ vs log ω plots and M″ vs log ω plots, respectively). Figs. 13 and 14 display the scaling behavior of ɛ″ and M″ at various temperatures for BMT and BZT. The perfect overlapping of these curves (excepting the low frequency region) recorded at different temperatures implies that the relaxation in the samples obeys the same mechanism at different temperatures in BMT and BZT ^[27]. The results of dielectric permittivity study indicate that for the present samples dipoles follow the applied field at low frequencies (where ω <<1/ τ) because the scaled curves do not overlap at low frequencies.

Fig. 13.

	Figure Option ViewDownloadNew Window
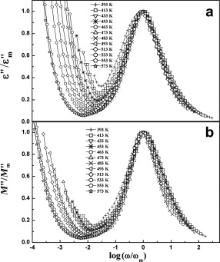	Fig. 13. Scaling behavior of ɛ″ (a) and M″ (b) at various temperatures for Ba(Mg1/3Ta2/3)O3.

Fig. 14.

	Figure Option ViewDownloadNew Window
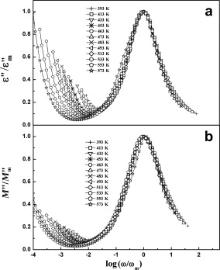	Fig. 14. Scaling behavior of ɛ″ (a) and M″ (b) at various temperatures for Ba(Zn1/3Ta2/3)O3.

The frequency dependence of normalized peaks of ɛ″/ ɛ″_m and M″/ M″_m vs log ω for BMT and BZT has been plotted ( Fig. 15). This formalism helps us to elucidate the nature of relaxation process. The overlapping of peak positions is the evidence of long-range (ionic or electronic) conduction process, on the other hand, peaks will not overlap for localized (defect) relaxation ^{[30] and [33]}. As in BMT and BZT both long-range and localized relaxation are present, therefore perfect overlapping between the normalized peaks does not occur.

Fig. 15.

	Figure Option ViewDownloadNew Window
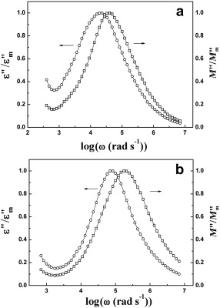	Fig. 15. Frequency dependence of normalized peaks of ɛ″/ ɛ″m and M″/ M″m vs log ω for Ba(Mg1/3Ta2/3)O3 at 393 K (a) and Ba(Zn1/3Ta2/3)O3 at 393 K (b).

It may be noted that at each temperature of measurement, a plateau has been observed in the ɛ′ vs log ω (Figs. 3(a) and 4(a)) and M′ vs log ω (Figs. 7(a) and 8(a)) plots of both the samples. This plateau shifts to the higher frequency with increasing temperature. The plateau observed in the ɛ′ vs log ω plot at 483 K ranges between 100 Hz and 700 Hz for BMT ( Fig. 3(a)) and from 100 Hz to 4.4 kHz for BZT ( Fig. 4(a)). For M′ vs log ω (Figs. 7(a) and 8(a)) plot at 483 K, the plateaus are observed within the same frequency ranges. Further to note that for BMT and BZT, the peak in tan δ vs log ω plot at 483 K is centered about 70 kHz ( Fig. 3(b)) and 146 kHz ( Fig. 4(b)), respectively while in the M″ vs log ω plot of BMT and BZT at 483 K, the peaks are observed at 100 kHz ( Fig. 7(b)) and 170 kHz ( Fig. 8(b)), respectively. Thus the characteristic frequency of BZT is greater than that of BMT. The temperature dependences of σ_dc and ω_m obtained from tan δ vs log ω plots obey the Arrhenius law. The ω_m obtained from M″ vs log ω plots also obeys the Arrhenius law. According to Arrhenius plots of σ_dc, the activation energies of BMT and BZT are 0.54 and 0.41 eV, respectively. The activation energies determined by using ω_m obtained from tan δ vs log ω plots are 0.54 and 0.40 eV, while that estimated by using ω_m obtained from M″ vs log ω plots are 0.55 and 0.38 eV, respectively for BMT and BZT. The nearly same activation energy for dc conductivity and dielectric relaxation as obtained from the temperature dependence of most probable relaxation time for tan δ indicates that the same charge carriers are responsible for dielectric relaxation and conductivity of the samples.

According to our previous study on A(Ni_1/3Ta_2/3)O₃ (where A = Ba, Ca and Sr) systems, the dielectric permittivity is the highest for barium nickel tantalate and the lowest for calcium nickel tantalate. It may be noted that the ionic radius are r_Ba > r_Sr > r_Ca. Taking account of our present and previous studies ^[33], we can conclude the dielectric permittivity of BNT > BMT ≈ BZT and the ionic radius of Zn ≈ Mg > Ni. It is therefore clear that in the case of complex perovskite oxides with general formula A( B′ B″)O₃, ionic radii of both A and B cations have significant influences on their dielectric properties. The dielectric permittivity of BMT and BZT are better than that of the A(Mg_1/3Nb_2/3)O₃ (where A = Ba, Ca and Sr) systems ^{[25], [26] and [27]}. The dielectric permittivity and the loss tangent are also comparable to that for A(Ni_1/3Ta_2/3)O₃ (where A = Ba, Ca and Sr) systems ^[36]. Our study also indicates that the dielectric properties of these compounds are improved significantly with increasing ionic radii of A cations but with decreasing ionic radii of B cations. The loss tangents of BMT and BZT are low. Therefore the samples may be utilized in various technological applications like capacitors, resonators, filters and integrated circuits.