Theoretical Investigation on Mechanical and Thermal Properties of a Promising Thermal Barrier Material: Yb3Al5O12

Cite this Article

Zhou Yanchun, Xiang Huimin, Feng Zhihai. Theoretical Investigation on Mechanical and Thermal Properties of a Promising Thermal Barrier Material: Yb₃Al₅O₁₂ . Journal of Materials Science & Technology, 2014, 30(7): 631-638 Copy to clipboard

Permissions

Theoretical Investigation on Mechanical and Thermal Properties of a Promising Thermal Barrier Material: Yb₃Al₅O₁₂

Zhou Yanchun^*, Xiang Huimin, Feng Zhihai

Science and Technology of Advanced Functional Composite Laboratory, Aerospace Research Institute of Materials and Processing Technology, Beijing 100076, China

Corresponding author. Prof., Ph.D.; Tel.: +86 10 68382478; Fax: +86 10 68383237

Abstract

An investigation on the mechanical and thermal properties of Yb₃Al₅O₁₂ is conducted by a combination of first-principles calculations and chemical bond theory calculation. Density functional theory (DFT) computations were performed for the structural, mechanical, and thermal properties, and the results are confirmed by chemical bond theory. Based on the calculated equilibrium crystal structure, heterogeneous bonding nature is revealed. The full set of elastic constants and mechanical properties of Yb₃Al₅O₁₂ are presented for the first time. The thermal expansion coefficient of Yb₃Al₅O₁₂ is calculated to be 7.5 × 10^-6 K^–1 by chemical bond theory. In addition, the minimum thermal conductivity of Yb₃Al₅O₁₂ is estimated to be 1.22 W m^-1 K^-1, and the origin of such low thermal conductivity is discussed. Our theoretical results highlight the potential of Yb₃Al₅O₁₂ as a prospective thermal barrier coating material.

Keyword: Thermal barrier coating; Ytterbium aluminum garnet; First principles calculations; Chemical bond theory

Show Figures

1. Introduction

The efficiency and power of gas-turbine engines used in transportation, energy, and defense sectors rely on the increase of the operated temperature ^[1]. To increase the operating temperatures of engines, efficient thermal barrier coatings (TBCs) are needed ^[2]. The current material of choice for TBCs is yttria-stabilized zirconia (YSZ) in its metastable tetragonal-prime structure ^[3]. However, the working temperature of YSZ is limited because the metastable tetragonal-prime structure becomes increasingly unstable at high temperature and is apt to decompose to a mixture of tetragonal and cubic zirconia ^[4]. Additionally, the oxygen diffusivity of YSZ is high at high temperature ^[5]. Therefore, new TBCs with superior high temperature properties are needed for both scientific significance and technological importance.

Experimental and theoretical trials reported recently have proved that yttrium aluminates, and yttrium aluminum garnet (i.e. Y₃Al₅O₁₂, YAG) in particular, are promising candidates for TBCs due to their superior high temperature stability, mechanical and thermal properties^{[6] and [7]}. At high temperature, YAG is stable with Al₂O₃ ^[6] that is the thermally grown oxide formed on Ni-based superalloys. High-temperature deformation tests on single-crystal YAG showed that YAG is one of the most creep-resistant, non-oxidizing material yet known^{[8] and [9]}. Recent theoretical results have confirmed the low thermal conductivity of YAG ^[10]. Thus, YAG is considered as a promising TBC material. However, Klemm et al. ^[11]found that the resistance of YAG to high temperature water corrosion is not quite satisfactory, which is adverse on the integrity and duration of coating. Therefore, materials with improved resistance to vapor corrosion are needed.

In the same work, Klemm et al. ^[11] reported that Yb₃Al₅O₁₂(YbAG), which shares the same structure with YAG, have superior resistance to vapor corrosion comparing with several other prospective TBC materials, such as Y₃Al₅O₁₂, Y₂Si₂O₇and Yb₂Si₂O₇. Having the same structure with YAG, YbAG is expected to possess similar excellent high temperature properties and lower minimum thermal conductivity due to the heavy atomic mass of Yb. Motivated by its potential high temperature applications, several works focused on the preparation of YbAG have been reported recently, by various approaches, such as co-precipitation method ^[12], micro-pulling-down technique ^[13], and RF-heating Czochralski method ^[14]. However, to the present authors' knowledge, the mechanical and thermal properties of YbAG have barely been reported. Clear understanding of mechanical and thermal properties and correlation of these properties to the structure of YbAG can provide valuable insights for the development of TBCs, and advance the applications of YbAG as high temperature structural component and TBC.

In this contribution, mechanical and thermal properties of Yb₃Al₅O₁₂were investigated from a combination of first-principles calculations and an empirical method based on chemical bond theory. The equilibrium crystal structure, second-order elastic coefficients, bulk modulus, shear modulus, Young's modulus, and Poisson's ratio were calculated by first-principles calculations. Then, the theoretical minimum thermal conductivity was estimated from modified Clarke's model^{[15] and [16]}, and the dependence of thermal conductivity of Yb₃Al₅O₁₂on temperature was predicted from Slack's model ^[17]. To valid the theoretical calculation, bulk modulus of Yb₃Al₅O₁₂ was estimated using chemical bond theory. The average linear thermal expansion coefficient (TEC) was also obtained using this empirical method. In the end, we highlight the potential application of Yb₃Al₅O₁₂as TBC.

2. Computation Methods

2.1. First-principles calculations

The first-principles calculations based on the density functional theory (DFT) were performed using the Cambridge Serial Total Energy Package (CASTEP) code ^[18]. Wherein the Norm-conserving pseudopotentials ^[19] were employed to represent the interactions between the ionic cores and the valence electrons for Yb, Al and O atoms. The electronic exchange-correlation energy was treated under the local density approximation (LDA) ^[20]. Feng et al. ^[21] investigated the effects of onsite Coulomb interaction ( U correction) on the electronic structures and mechanical properties of Re₂Zr₂O₇ pyrochlore. They found that the additional U correction only strongly affects the electronic structures of the rare-earth oxides, while the mechanical moduli are quite insensitive to the localization of partially filled 4f orbitals. Thus, the theoretical investigations in our work were conducted without consideration of U correction. The plane-wave basis set cut-off energy was fixed at 830 eV in all calculations after convergence test. The special points sampling integration over Brillouin zone are realized by using the Monkhorst–Pack method with special k-points meshes of 2 × 2 × 2 ^[22].

To get the equilibrium crystal structure, the lattice parameters and internal atomic coordinates were independently modified. The free enthalpy, interatomic forces and stresses of the unit cell were minimized under the Broyden–Fletcher–Goldfarb–Shanno (BFGS) minimization scheme ^[23]. The tolerances for geometrical optimization were: differences for total energy within 5 × 10^-6eV/atom, maximum ionic Hellmann–Feynman force within 0.1 eV/nm, maximum ionic displacement within 5 × 10^-5nm, and maximum stresswithin 0.02 GPa.

The theoretical elastic coefficients were determined from the first-principles strain–stress relationships method implemented by Milman et al. ^[24]. The criteria for convergence of optimization on atomic internal freedoms were selected as differences in the total energy within 1 × 10^-6eV/atom, Hellmann–Feynman force within 0.02 eV/nm, and maximum ionic displacement within 1 × 10^-5nm. The compliance tensor S was calculated as the inverse of the stiffness matrix, S = C^-1. The bulk modulus B and shear modulus G were calculated from the compliance tensor based on Voigt–Reuss–Hill approximation^{[25], [26] and [27]}. The Young's modulus E_H and Poisson's ratio ν were calculated using Hill's bulk modulus B_Hand shear modulus G_H by the following equations ^[28]:

(1)	$E = \frac{9 B_{H} G_{H}}{3 B_{H} + G_{H}}$

(2)	$ν = \frac{3 B_{H} - 2 G_{H}}{2 (3 B_{H} + G_{H})}$

According to Slack's model ^[17] and modified Clarke's model^{[15] and [16]}, the behavior of thermal conductivity at elevated temperatures of a material is accessible. Slack's model describes the intrinsic thermal conductivity of a material over wide range of temperatures, which is expressed as ^[17]:

(3)	$κ_{L} = A \frac{\bar{M} Θ^{3} δ}{γ^{2} n^{2 / 3} T}$

where A is a physical constant ( A ≈ 3.1 × 10^-6 if κ_L is in W m^-1K^-1, and δ in nm). $\bar{M}$ is the average mass of the atoms in the crystal, Θ is the Debye temperature, δ³ is the volume per atom, n is the number of atoms in the primitive unit cell, and γ , high temperature limit of the acousticphonon mode Grüneisen parameter, is a direct measure of the anharmonicity of phonon, and can be derived from Poisson's ratio ^[29]:

(4)	$γ = \frac{9 (υ_{l}^{2} - \frac{4}{3} υ_{s}^{2})}{2 (υ_{l}^{2} - 2 υ_{s}^{2})} = \frac{3}{2} (\frac{1 + ν}{2 - 3 ν})$

According to the modified Clarke's model^{[15] and [16]}, the theoretical lower limit of intrinsic thermal conductivity ( κ_min) can be calculated by:

(5)	$κ_{min} \to k_{B} υ_{m} {(\frac{M}{n d N_{AV}})}^{- 2 / 3}$

where k_B is the Boltzmann's constant, υ_mthe average sound velocity, N_AV the Avogadro's number, d the density, M the molecular weight, and n the number of atoms in the molecule. This modified model has been successfully applied to estimate the κ_min of several complex oxides, such as La₂T₂O₇ ^[16], M P₂O₇ ^[30], and MPO₄ ^[31].

The average sound velocity υ_m of a polycrystalline material is defined as ^[32]:

(6)	$υ_{m} = {[\frac{1}{3} (\frac{2}{υ_{s}^{3}} + \frac{1}{υ_{l}^{3}})]}^{- 1 / 3}$

where υ_l and υ_s are longitudinal and transverse sound velocities, respectively, which can be determined from the shear modulus G and the bulk modulus B by:

(7)	$υ_{l} = \sqrt{\frac{B + \frac{4 G}{3}}{d}}, and υ_{s} = \sqrt{\frac{G}{d}}$

The Debye temperature, Θ_D, was calculated according to the following equation ^[32]:

(8)	$Θ_{D} = \frac{h}{k_{B}} {[\frac{3 n}{4 π} (\frac{N_{AV} d}{M})]}^{1 / 3} υ_{m} = C l υ_{m}$

where h is the Plank's constant. $l = {(n d / M)}^{1 / 3}$ is defined as the linear density and $C = h / k_{B} {(3 N_{AV} / 4 π)}^{1 / 3}$ is a constant.

2.2. Chemical bond theory

Developed by Phillips ^[33], Van Vechten ^[34], Levine ^[35], and Zhang et al. ^[36], complex chemical bond theory (CBT) provides a simple but efficient approach to study the characteristic of chemical bonds in complex materials, and to predict related physical properties of a crystal from the viewpoint of bonding. The implementation of this theory relies on the decomposition of complex crystal into a linear combination of subformula of various binary crystals ^[36].

For a giving chemical formula of a complex crystal, CBT provides an efficient way to decompose it into the following simple subformula ^[36]:

(9)	$A_{a 1}^{1} A_{a 2}^{2} \dots A_{a i}^{i} B_{b 1}^{1} B_{b 2}^{2} \dots B_{b j}^{j} = \sum_{i, j} A_{m i}^{i} B_{n j}^{j} = \sum_{μ} {(A_{m} B_{n})}^{μ}$

(10)	$m i = \frac{N (B^{j} - A^{i}) \times a i}{N_{C} (A^{i})}, n j = \frac{N (A^{i} - B^{j}) \times b j}{N_{C} (B^{j})}$

where N_C( Aⁱ) and N_C( B^j) represent the coordination numbers of Aⁱand B^jions in the crystal. N ( B^j- Aⁱ) is the nearest coordination fraction contributed by Aⁱion and vice versa. ( A_m B_n)^μis the μ type of subformulas.

For every fictitious binary crystal ( A_m B_n)^μdecomposed according to CBT, the total lattice energy U^μ can be separated into the ionic part $(U_{i}^{μ})$ and the covalent part $(U_{c}^{μ})$ , which can, respectively, be expressed as ^[37]:

(11)	$U_{i}^{μ} = \frac{1270 (m + n) Z^{+} Z^{-}}{l^{μ}} (1 - \frac{0.4}{l^{μ}}) f_{i}^{μ} (kJ \cdot {mol}^{- 1})$

(12)	$U_{c}^{μ} = 2100 m \frac{{(Z^{+})}^{1.64}}{{(l^{μ})}^{0.75}} f_{c}^{μ} (kJ \cdot {mol}^{- 1})$

where Z⁺ and Z^- are the valence of cation and anion in the binary crystal, l^μ is the length of μ type bond. $f_{i}^{μ}$ and $f_{c}^{μ}$ are the ionicity and covalency of A – B bond, and are defined as ^[35]:

(13)	$f_{i}^{μ} = \frac{{(C^{μ})}^{2}}{{(E_{g}^{μ})}^{2}}, f_{c}^{μ} = \frac{{(E_{h}^{μ})}^{2}}{{(E_{g}^{μ})}^{2}}$

(14)	$f_{i}^{μ} + f_{c}^{μ} = 1$

where $E_{g}^{μ}$ is the average energy bond gap and is composed of homopolar $(E_{h}^{μ})$ and heteropolar ( C^μ) parts. These two parts of energy can be estimated by ^[35]:

(15)	$E_{h}^{μ} = \frac{39.74}{{(l^{μ})}^{2.48}} (eV)$

(16-a)

C^{μ} = 14.4 b^{μ} \exp (- k_{s}^{μ} r^{μ}) (\frac{{(Z_{A}^{μ})}^{*}}{r^{μ}} - (n / m) \frac{{(Z_{B}^{μ})}^{*}}{r^{μ}}) (eV) (if n > m)

(16-b)

C^{μ} = 14.4 b^{μ} \exp (- k_{s}^{μ} r^{μ}) ((m / n) \frac{{(Z_{A}^{μ})}^{*}}{r^{μ}} - \frac{{(Z_{B}^{μ})}^{*}}{r^{μ}}) (eV) (if m > n)

where b^μ is a structural correction factor, r^μ = l^μ /2 is the average ion radius expressed in angstroms, $\exp (- K_{s}^{μ} r^{μ})$ is the Thomas–Fermi screening factor, where $K_{s}^{μ}$ is a parameter related to the Bohr radius, ${(Z_{A}^{μ})}^{*}$ and ${(Z_{B}^{μ})}^{*}$ are the effective valence electron numbers of A and B ions, respectively.

The lattice energy density u^μ of a binary crystal, which is an essential parameter in estimating the bulk modulus and linear thermal expansion coefficient of a binary crystal, is defined as ^[38]:

(17)	$u^{μ} = \frac{U^{μ}}{N_{Av} n^{μ} v_{b}^{μ}}$

where n^μ is the number of the chemical bond in oneformula unit, $v_{b}^{μ}$ is the volume of μ type chemical bond. Then the bulk modulus B^μ of a certain type of binary crystals can be calculated on the basis of lattice energy density ^[38]:

(18)	$B^{μ} = δ^{μ} + \frac{u^{μ}}{β^{μ}}$

where δ^μ is a constant, and β^μ is a proportion factor depending on the average valence and average coordination number of subformula A_m B_n. The bulk modulus of the complex crystals is expressed as ^[39]:

(19)	$B = \frac{1}{k}$

(20)	$k = \frac{Δ V}{V_{m} Δ P} = \frac{1}{V_{m}} \sum_{μ} \frac{Δ V_{μ}}{Δ P_{μ}} = \frac{1}{V_{m}} \sum_{μ} V^{μ} k^{μ} = \frac{1}{V_{m}} \sum_{μ} \frac{V^{μ}}{B^{μ}}$

where B and B^μ are the bulk modulus of the material and μ type chemical bond, respectively, and V_m and V^μ are the volume of one molecule and μ type bond in one molecule, respectively.

The linear TEC of a complex crystal is closely related to the lattice energy and can be estimated by the following equations ^[40]:

(21)	$α = \sum_{μ} F^{μ} α^{μ}$

α^{μ} = - 3.1685 + 0.8376 χ^{μ}

(23)

χ^{μ} = \frac{k_{B} Z_{A}^{μ} N_{CA}^{μ}}{U^{μ} Δ^{μ}} β^{μ}, β^{μ} = \frac{m (m + n)}{2 n}

where parameter Δ^μ is a correction parameter from the analysis of experimental results, which depends on the position of cation in the periodic table. F^μ is the fraction of μ type bond in the complex crystal.

3. Results and Discussion

3.1. Structural and chemical bonding properties

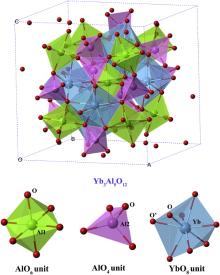
As shown in Fig. 1, the crystal structure of Yb₃Al₅O₁₂ which crystallizes in Ia $\bar{3}$ d space group is constructed by three basic units: dodecahedrally bonded Yb atoms, octahedrally and tetrahedrally bonded Al atoms. The structures of constructive polyhedra are also shown in Fig. 1 for a clear insight into the crystal structure. For Yb₃Al₅O₁₂, there are 160 atoms in one unit cell ( Z = 8), which consist of one Yb site, two Al sites and one O site. The position of each nonequivalent atom is shown in Table 1. For convenience, we labeled octahedrally bonded Al atom as Al1 and tetrahedrally bonded Al atom as Al2.

	Figure Option View Download New Window
	Fig. 1. Crystal structure of Yb₃Al₅O₁₂ and typical constructive units in Yb₃Al₅O₁₂.

Table 1. Theoretical and experimental lattice parameters of Yb₃Al₅O₁₂

The calculated lattice parameters of Yb₃Al₅O₁₂ are listed in Table 1, together with previously reported experimental data ^[41] for comparison. As shown in Table 1, the calculated lattice parameter a is about 0.28% smaller than the experimental data. The atomic position of O atom is quite consistent with the reported one. Good coincidence between the theoretical results and the experimental ones ensures the reliability of our calculations.

The Mulliken analysis on Yb–O and Al–O bonds of Yb₃Al₅O₁₂is also conducted by DFT calculations, and listed in Table 2. The bond lengths and Mulliken population of Yb–O and Al–O bonds of another rare-earth aluminate with the same structure, Y₃Al₅O₁₂, is also included for comparison ^[10]. For both aluminates, the Mulliken population of Al–O bonds are higher than that of Yb/Y–O bonds, indicating higher level of covalency of Al–O bonds. Moreover, two types of Al–O bonds are quite different in bond length and Mulliken population, demonstrating that bond strength and covalency of Al–O in different polyhedra are quite different from each other.

Table 2. Mulliken population and bond lengths of different bonds in Y₃Al₅O₁₂ and Yb₃Al₅O₁₂

For Yb₃Al₅O₁₂, the chemical bonds are diverse in length and covalency, the bond strength and bond energy are anticipated to be miscellaneous. To quantify this diversity, the chemical parameters, such as covalency and bond energy, of each bond are calculated using CBT. First, based on the analysis on the crystal structure, the chemical formula of Yb₃Al₅O₁₂is decomposed into the following subformulas:

Yb₃Al₅O₁₂=YbAl(1)Al(2)O=Yb_3/2O₃+Yb_3/2O₃′ +Al(1)₂O₃+Al(2)₃O₃ (24)

where the superscripts in the formula mark the oxygen atoms having the same crystallography site with different bond lengths in one polyhedron. Then, the desired parameters of subformula are calculated by Eqs. (11), (12), (13), (14), (15), and) and are listed in Table 3. The bond lengths ( l^μ) of all bonds used in the calculation of bond parameters are from the previously reported experimental data ^[41]. For all these bonds, the heteropolar part of energies ( C^μ) are substantially larger than the homopolar part of energies $(E_{h}^{μ})$ , which indicates complex and more ionic bonding nature of these bonds. The calculated covalency $(f_{c}^{μ})$ of Al–O bonds is distinctly larger than that of Yb–O bonds, and covalency of Al–O bond in tetrahedron is also larger than that of Al–O bond in AlO₆ octahedron. These results are consistent with the Mulliken analysis on the bonds. In addition, the bond energies of Al–O bonds are significantly larger than those of Yb–O bonds, showing strong bonding nature of Al–O bonds compared with Yb–O bonds. It is notable that the bond energies of Al–O bonds in AlO₄ unit are considerably larger than those in AlO₆unit, indicating that adding two O atoms to the tetrahedral structure decreases the bonding strength of original Al–O bonds significantly. This can also be testified simply by Pauling's rules ^[42]: the strength of a bond equals the ionic valence divided by the coordination number, which yields a strength of 0.125 for Yb–O bonds in YbO₈dodecahedron, 0.167 for Al–O bonds in AlO₆octahedron, and 0.25 for Al–O bonds in AlO₄tetrahedron.

Table 3. Chemical parameters of subformulas for Yb₃Al₅O₁₂ by chemical bond theory

Bond	l^μ (nm)	C^μ (eV)	$E_{h}^{μ}$ (eV)	$f_{i}^{μ}$	$f_{c}^{μ}$	U^μ (kJ mol^-1)
Yb–O	0.2283	15.56	5.10	0.90	0.10	9387
Yb–O′	0.2416	13.68	4.43	0.91	0.09	8974
Al(1)–O	0.1917	16.54	7.86	0.82	0.18	15708
Al(2)–O	0.1763	11.73	9.67	0.60	0.40	28001

Table 3. Chemical parameters of subformulas for Yb₃Al₅O₁₂ by chemical bond theory

In general, the bonding nature is diverse and heterogeneous in Yb₃Al₅O₁₂ though it crystallizes in cubic structure. Al–O units are strongly constructed and show rigid characteristic while YbO₈ dodecahedron is relatively weak and soft. These structural features play an essential role in the elastic and thermal properties of this material, which will be discussed in the following sections.

3.2. Elastic properties

To disclose the mechanical properties of Yb₃Al₅O₁₂, which are closely related to the characteristic of crystal structure, the full sets of independent second-order elastic constants were calculated first. To the author's knowledge, the full sets of elastic constants of ytterbium aluminate have not been reported experimentally or theoretically so far. The calculated elastic constants are listed in Table 4, accompanied by those of Y₃Al₅O₁₂as comparison. The mechanical stability of a crystal structure can be justified from the Born–Huang criterion ^[43]. For a cubic structure, the conditions could be expressed as: c₄₄>0, c₁₁>| c₁₂|, and c₁₁+ 2 c₁₂>0. The criterions are completely satisfied by Yb₃Al₅O₁₂, demonstrating its stability under elastic strain perturbations. Among all constants, c₁₁represents the stiffness against principal strains while c₄₄corresponds to resistance to shear deformation. A common feature for both materials is that c₁₁is much higher than c₄₄, indicating less resistance of these two compounds to the shear deformation.

Table 4. Theoretical second-order elastic constants c_ij (in GPa), and Zener ratio ( A) of Yb₃Al₅O₁₂ ceramic. The experimental data for single-crystal Y₃Al₅O₁₂ is also included for comparison

The calculated elastic constants are used to estimate the mechanical properties, i.e. bulk and shear moduli, Poisson's ratio and Young's modulus, according to Voigt–Reuss–Hill approximation^{[25], [26] and [27]}. The calculated mechanical properties are tabulated in Table 5. However, no experimental data are available for Yb₃Al₅O₁₂. Therefore, to verify our first principle calculation, the bulk modulus of Yb₃Al₅O₁₂is also estimated using CBT. The calculated results are listed in Table 6. It is obvious that the bulk moduli for Al–O bonds are enormously larger than those of Yb–O bonds, showing less compressibility of Al–O bonds. The bulk modulus for polycrystal is estimated to be 164 GPa, which shows an excellent agreementwith the value (163 GPa) calculated by first-principles.

Table 5. Theoretical bulk modulus B_H (GPa), shear modulus G_H (GPa), Young's modulus E (GPa), Poisson's ratio ( ν) and Pugh's ratio ( G/B) of Yb₃Al₅O₁₂ ceramic

Table 6. Estimation of bond volume ν^μ (10^-3 nm³), lattice energy density u^μ (GPa), bulk modulus B (GPa) and linear thermal expansion coefficient α (×10^-6 K^–1) of Yb₃Al₅O₁₂ from chemical bond theory

Shear modulus G describes the resistance of a material against a shape change. For both materials, the shear moduli are quite smaller than the bulk modulus, indicating low resistance to shear deformation, as shown in Table 5. The G/B ratio (namely Pugh's ratio) is 0.64 and 0.60 for Yb₃Al₅O₁₂ and Y₃Al₅O₁₂, respectively. It is widely accepted that the ductility of a material could be reflected by Pugh's ratio. A low (high) Pugh'sratio value is associated with ductility (brittleness). The Pugh's ratios of SiC, a brittle ceramic, are 0.85 ^[44], and 0.76 for ZrC ^[45], while for a typical ductile ceramic, Ti₃SiC₂, it is 0.65 ^[46]. The Pugh's ratios of Yb₃Al₅O₁₂and Y₃Al₅O₁₂ are close to that of Ti₃SiC₂, indicating the possible damage tolerance for their low shear moduli.

The intrinsic hardness of a material is a highly complex property, which is difficult to describe with a formal theoretical definition. Chen et al. ^[47]proposed an empirical model, which is correlated not only with shear modulus G , but also with bulk modulus B. In their model, the Vickers hardness ( H_V) is estimated by the following formula:

H_{V} = 2 {(k^{2} G)}^{0.585} - 3

where k is the Pugh's modulus ratio. They found that their model performed well across a large class of materials and hardness values ^[47]. Based on chemical bond theory, Gao et al. ^[48]proposed another empirical equation to estimate hardness of covalent crystals:

(26)

H_{v} = {[\prod_{μ} {(H_{v}^{μ})}^{n^{μ}}]}^{1 / \sum_{μ} n^{μ}}

where $H_{v}^{μ} = 350 {(N_{e}^{μ})}^{2 / 3} \exp (- 1.191 f_{i}^{μ}) / {(l^{μ})}^{2.5}$ is the hardness of binary compound, the other parameters have already been described in Sectionand in Ref. [51]. Here, we employ these two models to estimate the hardness of Yb₃Al₅O₁₂. The hardness of Yb₃Al₅O₁₂is 14.9 GPa from Chen's model, and 13.1 GPa from Gao's model. The hardness estimated from two different models is quite consistent with each other, showing the reliability of our estimations. Compared to Ti₃SiC₂, relatively high hardness of Yb₃Al₅O₁₂suggests poor machinability of this material.

Young's modulus of polycrystalline Yb₃Al₅O₁₂is 257 GPa according to Eq. (1). Based on the structure shown in Fig. 1, the orientation of Yb–O bonds and Al–O bonds in space is quite random, which may result in anisotropy in elastic behavior. To get a clear and complete representation of the elastic anisotropy of Yb₃Al₅O₁₂, the variation of Young's modulus as a function of crystal orientation is investigated. The direction-dependence of Young's modulus, E , for Yb₃Al₅O₁₂is given by the following equation ^[49]:

(27)	$\frac{1}{E} = s_{11} - 2 (s_{11} - s_{12} - \frac{1}{2} s_{44}) (l_{1}^{2} l_{2}^{2} + l_{1}^{2} l_{3}^{2} + l_{2}^{2} l_{3}^{2})$

where s₁₁, s₁₂, and s₄₄ are the elastic compliances; l₁, l₂, and l₃ are the directional cosines of angles with the three principal directions, respectively.

The three-dimensional surface contour of Young's modulus of Yb₃Al₅O₁₂in full space is shown in Fig. 2(a), and the planar projection of Young's modulus on {110} crystallographic planes, which include all three of the principal directions of a cubic crystal:<100>, <110>, and<111>, is also shown in Fig. 2(b). The elastic anisotropy of Yb₃Al₅O₁₂is quite unobvious. The three-dimensional surface of Young's modulus is nearly a sphere, and the projection on {110} planes is close to a circle. The maximum and minimum of Young's modulus are 266 GPa and 246 GPa, which are along<100>and<111>direction, respectively. Young's modulus in<110>direction is 260 GPa. The minimum is only 7.5% smaller than the maximum. The isotropy of Young's modulus is also identified by Zener ratio A ^[50], which is defined as: A = 2 c₄₄/( c₁₁– c₁₂). A = 1 is defined to indicate elastic isotropy, i.e., when c₄₄= ( c₁₁– c₁₂)/2. The value of this ratio from cubic elastic constants also determines the direction for the extreme of Young's modulus (i.e., for A <1 the maximum Young's modulus would be in the<100>directions, and for A >1 the maximum would be in the<111>directions). For Yb₃Al₅O₁₂, Zener ratio is 1.10, which is slightly larger than 1. This confirms the isotropy of elastic behavior of Yb₃Al₅O₁₂. Interestingly, the value of Zener ratio for Y₃Al₅O₁₂is 1.03, which is also slightly larger than 1. Therefore, it is reasonable to conclude that Y₃Al₅O₁₂is also isotropic in elastic behavior and the maximum of Young's modulus is also along<111>directions. The isotropy in mechanical behavior of Y₃Al₅O₁₂has been confirmed by previous experimental observation ^[9].

	Figure Option 3Al₅O₁₂ and (b) planar projections on $(1 \bar{1} 0)$ crystallographic plane. '>View Download New Window
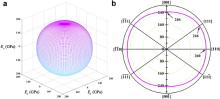3Al₅O₁₂ and (b) planar projections on $(1 \bar{1} 0)$ crystallographic plane. '>	Fig. 2. (a) Surface contour of directional dependent Young's modulus of Yb₃Al₅O₁₂ and (b) planar projections on $(1 \bar{1} 0)$ crystallographic plane.

In the investigations and applications of a material, the orientation of grains plays a critical role in determining the mechanical performance of a material, because the anisotropy in elastic behavior generally exists, even in materials with cubic crystal structure (Zener ratio of ZrO₂is 0.37–0.52, 0.44–0.59 for HfO₂, 0.54–0.77 for M P₂O₇, 1.49 for MgO, and 2.43 for spinel)^{[30] and [51]}. Fig. 2shows the isotropy of the elastic properties of Yb₃Al₅O₁₂and also indicates that the difference of expected fracture energy in different orientations is quite limited. Thus, there is no need to consider the anisotropy of elasticity in the application of Yb₃Al₅O₁₂, which is positive to promote the potential of applications as structural component and coating.

3.3. Thermal properties

TEC is a fundamental parameter for a material. Several approaches have been proposed to estimate TEC theoretically: quasi-harmonic approximation (QHA) ^[52], molecular dynamics (MD) ^[53], CBT ^[40] etc. The CBT proposed by Zhang et al. ^[40] is a simple empirical method to predict the linear expansion coefficients of complex crystals based only on the crystal structure data. They had used this simple method to evaluate the TEC of Y₃Al₅O₁₂ ^[40], and the estimated result showed excellent agreement with experimental data. Therefore, the linear TEC of Yb₃Al₅O₁₂is evaluated by CBT in our work. The calculated results are listed in Table 6. Considering that the bond strength of Al–O bonds in AlO₄ tetrahedron is substantially higher than those of the other bonds, it is not surprising that the contribution from Al–O bonds of AlO₄ tetrahedron is quite smaller than those from the other bonds. The TEC of Yb₃Al₅O₁₂ is 7.5 × 10^-6K^–1, theoretically. Experimentally, however, measurement on TEC of Yb₃Al₅O₁₂has barely conducted. Compared with the theoretical TEC of Y₃Al₅O₁₂, 7.98 × 10^-6K^–1, obtained by Zhang et al. ^[40], the TEC of Yb₃Al₅O₁₂is slightly smaller. This can be comprehended from the structure of these two compounds. With a same coordination number of 8, the ion radii ^[54] of Y³⁺ (102 pm) is larger than that of Yb³⁺(98 pm) owing to the contraction of the 4f shell. With smaller ion radius, Yb–O bonds are supposed to be stronger than Y–O bonds, which would result in smaller TEC.

As shown in Eqs. (3)and (5), estimation of the intrinsic thermal conductivity of Yb₃Al₅O₁₂relies on the knowledge of sound velocities ( υ_l, υ_s, υ_m), Debye temperature ( Θ_D), and Grüneisen parameter ( γ). The sound velocities and Debye temperature are derived from obtained elastic moduli and density of equilibrium structure by Eqs. (6), (7) and (8). The calculated parameters for Yb₃Al₅O₁₂are listed in Table 7, together with those of Y₃Al₅O₁₂for comparison. It is reasonable that the sound velocities of Yb₃Al₅O₁₂ are significantly lower than those of Y₃Al₅O₁₂ since higher value of density results in smaller sound velocities. Relatively low Debye temperature of Yb₃Al₅O₁₂ also suggests relatively weak atomic vibrations in the lattice due to heavy atomic weight of Yb atom, comparing with Y₃Al₅O₁₂.

Table 7. Theoretical density d (in g cm^-3), sound velocities ( υ_l, υ_s, υ_m in km s^-1), Debye temperature Θ_D (in K), Grüneisen parameter γ , and minimum thermal conductivity (in W m^-1 K^-1) of Yb₃Al₅O₁₂ and Y₃Al₅O₁₂ ceramics. The Grüneisen parameter of Y₃Al₅O₁₂ is calculated from the reported Poisson's ratio

At relatively high temperature, the dominant mechanism of phonon scattering, which determines the intrinsic lattice thermal conductivity of a material, is the Umklapp processes, in which the acoustic phonon branches interact with each other to transport heat. Slack's model (i.e. Eq. (3)) ^[17]is a suitable approach to describe the temperature dependence of thermal conductivity when the Umklapp scattering is dominant. The temperature dependence of thermal conductivity of Yb₃Al₅O₁₂estimated from Slack's model is shown in Fig. 3. The thermal conductivity of Yb₃Al₅O₁₂decreases with temperature. With the temperature increases further, the thermal conductivity would approach a minimum when the phonon mean-free path decreased to the average atomic distance ^[15]. The minimum thermal conductivity κ_min can be evaluated by modified Clarke's model, as illustrated by Eqs. (5) and (6). The minimum thermal conductivity of Yb₃Al₅O₁₂ was predicted to be 1.22 W m^-1K^-1. Combining these two models, the behavior of thermal transportation of Yb₃Al₅O₁₂ can be described as that, with increasing the temperature, the thermal conductivity of Yb₃Al₅O₁₂declines as κ = 1480.18/ T , and at around 1200 K, it reaches a minimum value and then keeps unchanged with increasing temperature.

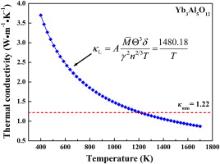	Figure Option View Download New Window
	Fig. 3. Temperature dependence of thermal conductivity of Yb₃Al₅O₁₂. Theoretical minimum thermal conductivity (red dash line) is also shown.

The minimum thermal conductivity of Yb₃Al₅O₁₂is 1.22 W m^-1K^-1, which is 23% smaller than that of Y₃Al₅O₁₂. Zhan et al. ^[10] theoretically investigated the thermal conductivity of Y₃Al₅O₁₂. They concluded that the origin of low thermal conductivity of Y₃Al₅O₁₂ was mainly attributed to the heterogeneous bond strength. The softer Y–O polyhedra are equivalent to the thermal rattle structures, and provide “weak zones” that scatter phonons and reduce phonon mean free path. These structure features are also applicable to Yb₃Al₅O₁₂, Yb–O polyhedra also provide “weak zone” to scatter phonons. In addition, as suggested by Clarke ^[15], the strongest influence on the minimum thermal conductivity is the ratio of the atomic weight to the number of atoms per molecule, i.e. mean atomic weight M/n in Eq. (5). The mean atomic weight of Yb₃Al₅O₁₂(42.3 amu/atom) is 30% larger than that of Y₃Al₅O₁₂(29.7 amu/atom), which results in lower thermal conductivity of Yb₃Al₅O₁₂.

The major criterion for a prospective TBC material is low intrinsic thermal conductivity. Besides, several additional selection criteria have also been proposed by Clarke ^[15]. First of all, TBC material must be thermodynamically stable with Al₂O₃ since the majority of TBCs are used in conjunction with alumina-forming alloys. For Yb₃Al₅O₁₂, it is stable with alumina till they melt at around 2100 K ^[55]. Second, TBC material should not exhibit appreciable mass loss at high temperatures, especially in the presence of water vapor. As reported by Klemm ^[11], the surface corrosion rate of Yb₃Al₅O₁₂ in hot gas environments is appreciably smaller than those of several other prospective TBC materials, such as Y₃Al₅O₁₂, Y₂Si₂O₇ and Yb₂Si₂O₇. Moreover, as the weight of a coating increases linearly with both its thickness and density, a key factor affecting the design of TBC is the specific thermal conductivity, namely the product of thermal conductivity and the density. The specific thermal conductivity of Yb₃Al₅O₁₂(8.14) is smaller than that of yttria-stabilized zirconia (9.31) ^[56], the most successful and commercialized thermal barrier material.Good stability with alumina at moisture environments and small specific thermal conductivity ensure Yb₃Al₅O₁₂ a prospective candidate as coating TBC material.

4. Conclusion

In this work, bonding characteristics, elastic stiffness, and thermal conductivity of Yb₃Al₅O₁₂ were investigated by first-principles calculations and CBT. The theoretical results reveal the heterogeneous bonding nature of Yb₃Al₅O₁₂, i.e. Al–O bonds are stronger than Yb–O bonds. The second-order elastic constants and mechanical properties of Yb₃Al₅O₁₂ were calculated. Low shear modulus G suggests shear deformation resistance of Yb₃Al₅O₁₂is low and damage tolerance. The hardness of Yb₃Al₅O₁₂is 14.9 GPa from calculated elastic moduli, which is consistent with the hardness (13.1 GPa) estimated from CBT. Relatively high hardness indicates poor machinability of Yb₃Al₅O₁₂. Yb₃Al₅O₁₂ shows isotropy in elastic behavior based on the discussion of direction dependence of Young's modulus. Using CBT, the TEC of Yb₃Al₅O₁₂ is estimated to be 7.5 × 10^-6K^–1. The temperature dependence of thermal conductivity of Yb₃Al₅O₁₂ is predicted based on the obtained elastic moduli, sound velocities and Debye temperature. The intrinsic thermal conductivity of Yb₃Al₅O₁₂ decreases as 1480.18/ T and approaches a minimum thermal conductivity (1.22 W m^-1K^-1) at high temperatures. Weak Yb–O bonds and large mean atomic weight contribute to the low thermal conductivity. Our theoretical results highlight the potential of Yb₃Al₅O₁₂as a promising TBC material.

Acknowledgments

This work was supported by the National Outstanding Young Scientist Foundation for Y.C. Zhou under Grant No. 59925208, and the National Natural Science Foundation of China under Grant No. 50832008.

The authors have declared that no competing interests exist.

Reference

View Option

1.	D. R. Clarke, C. G. Levi, Annu. Rev. Mater. Res. , 33 (2003), pp. 383–417 [Cited within: 1]
2.	D. R. Clarke, S. R. Phillpot, Mater. Today, 8 (2005), pp. 22–29 [Cited within: 1] [JCR: 6.071]
3.	A. J. Slifka, B. J. Filla, J. M. Phelps, G. Bancke, C. C. Berndt, J. Therm, Spray Technol. , 7 (1998), pp. 43–46 [Cited within: 1]
4.	R. A. Miller, J. L. Smialek, R. G. Garlick, , in: A. H. Heuer, L. W. Hobbs (Eds. ), Advances in Ceramics, Science and Technology of Zirconia, Vol. 3, American Ceramic Society, Columbus, OH (1981), pp. 241–251 [Cited within: 1]
5.	P. Ramaswamy, S. Seetharamu, K. B. R. Varma, K. J. Rao, J. Therm, Spray Technol. , 7 (1998), pp. 497–504 [Cited within: 1]
6.	Y. Harada, T. Suzuki, K. Hirano, N. Nakagawa, Y. Waku, J. Eur. Ceram. Soc. , 25 (2005), pp. 1275–1283 [Cited within: 2] [JCR: 2.36]
7.	P. Djemia, F. Tétard, K. Bouamama, E. Charron, D. Tétard, Y. Rabinovitch, J. Eur. Ceram. Soc. , 27 (2007), pp. 4719–4725 [Cited within: 1] [JCR: 2.36]
8.	G. S. Corman, Ceram. Eng. Sci. Proc. , 12 (1991), pp. 1745–1766 [Cited within: 1]
9.	G. S. Corman, J. Mater. Sci. Lett. , 12 (1993), pp. 379–382 [Cited within: 2] [JCR: 0.711]
10.	X. Zhan, Z. Li, B. Liu, J. Y. Wang, Y. C. Zhou, Z. J. Hu, J. Am. Ceram. Soc. , 95 (2012), pp. 1429–1434 [Cited within: 3] [JCR: 2.107]
11.	H. Klemm, J. Am. Ceram. Soc. , 93 (2010), pp. 1501–1522 [Cited within: 3] [JCR: 2.107]
12.	Y. Wu, J. Li, Y. Pan, Q. Liu, J. Guo, Ceram. Int. , 35 (2009), pp. 25–27 [Cited within: 1] [JCR: 1.789]
13.	V. I. Chani, A. Yoshikawa, H. Machida, T. Fukuda, Mater. Sci. Eng. B, 75 (2003), pp. 53–60 [Cited within: 1] [JCR: 1.846]
14.	X. Xu, Z. Zhao, J. Xu, P. Deng, J. Cryst. Growth, 257 (2003), pp. 272–275 [Cited within: 1] [JCR: 1.552]
15.	D. R. Clarke, Surf. Coat. Technol. , 163–164 (2003), pp. 67–74 [Cited within: 6] [JCR: 1.941]
16.	B. Liu, J. Y. Wang, F. Z. Li, Y. C. Zhou, Acta Mater. , 58 (2010), pp. 4369–4377 [Cited within: 4] [JCR: 3.941]
17.	G. A. Slack, J. Phys. Chem. Solids, 34 (1973), pp. 321–335 [Cited within: 4] [JCR: 1.527]
18.	M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark, M. C. Payne, J. Phys. Condens. Matter, 14 (2002), pp. 2717–2743 [Cited within: 1] [JCR: 2.355]
19.	J. S. Lin, A. Qteish, M. C. Payne, V. Heine, Phys. Rev. B, 47 (1993), pp. 4174–4180 [Cited within: 1]
20.	D. M. Ceperley, B. J. Alder, Phys. Rev. Lett. , 45 (1980), pp. 566–569 [Cited within: 1] [JCR: 7.943]
21.	J. Feng, B. Xiao, C. L. Wan, Z. X. Qu, Z. C. Huang, J. C. Chen, R. Zhou, W. Pan, Acta Mater. , 59 (2011), pp. 1742–1760 [Cited within: 1] [JCR: 3.941]
22.	H. J. Monkhorst, J. D. Pack, Phys. Rev. B, 13 (1976), pp. 5188–5192 [Cited within: 1]
23.	B. G. Pfrommer, M. Côté, S. G. Louie, M. L. Cohen, J. Comput. Phys. , 131 (1997), pp. 233–240 [Cited within: 1] [JCR: 2.138]
24.	V. Milman, M. C. Warren, J. Phys. Condens. Matter, 13 (2001), pp. 241–245 [Cited within: 1] [JCR: 2.355]
25.	W. Voigt Lehrbuch der Kristallphysik, Leipzig, Taubner (1928) [Cited within: 2]
26.	A. Reuss, Z. Angew, Math. Mech. , 9 (1929), pp. 49–58 [Cited within: 2] [JCR: 1.415]
27.	R. Hill, Proc. Phys. Soc. A, 65 (1952), pp. 349–354 [Cited within: 2]
28.	D. J. Green An Introduction to the Mechanical Properties of Ceramics, Cambridge University Press, Cambridge (1993) [Cited within: 1]
29.	B. D. Sand itov, S. B. Tsydypov, D. S. Sand itov, Acoust. Phys. , 53 (2007), pp. 594–597 [Cited within: 1] [JCR: 0.421]
30.	H. M. Xiang, F. Z. Hai, Y. C. Zhou, J. Eur. Ceram. Soc. , 34 (2014), pp. 1809–1818 [Cited within: 2] [JCR: 2.36]
31.	Y. C. Zhou, B. Liu, J. Eur. Ceram. Soc. , 33 (2013), pp. 2817–2821 [Cited within: 1] [JCR: 2.36]
32.	O. L. Anderson, J. Phys. Chem. Solids, 24 (1963), pp. 909–917 [Cited within: 2] [JCR: 1.527]
33.	J. C. Phillips, J. A. V. Vechten, Phys. Rev. Lett. , 22 (1969), pp. 705–708 [Cited within: 1] [JCR: 7.943]
34.	J. A. V. Vechten, Phys. Rev. , 182 (1969), pp. 891–905 [Cited within: 1] [JCR: 7.943]
35.	B. F. Levine, J. Chem. Phys. , 59 (1973), pp. 1463–1486 [Cited within: 3] [JCR: 1.578]
36.	D. Xue, S. Zhang, J. Phys. Condens. Matter, 8 (1996), pp. 1949–1956 [Cited within: 3] [JCR: 2.355]
37.	D. Liu, S. Zhang, Z. Wu, Inorg. Chem. , 42 (2003), pp. 2465–2469 [Cited within: 1] [JCR: 4.593]
38.	S. Zhang, H. Li, H. Li, S. Zhou, X. Cao, J. Phys. Chem. B, 111 (2007), pp. 1304–1309 [Cited within: 2] [JCR: 3.607]
39.	S. Zhang, H. Li, L. Li, S. Zhou, Appl. Phys. Lett. , 91 (2007), p. 251905 [Cited within: 1] [JCR: 3.794]
40.	S. Zhang, H. Li, S. Zhou, T. Pan, Jpn. J. Appl. Phys. , 45 (2006), pp. 8801–8804 [Cited within: 5] [JCR: 1.067]
41.	L. Dobrzycki, E. Bulska, D. A. Pawlak, Z. Frukacz, K. Wozniak, Inorg. Chem. , 43 (2004), pp. 7656–7664 [Cited within: 2] [JCR: 4.593]
42.	L. Pauling, J. Am. Chem. Soc. , 51 (1929), pp. 1010–1026 [Cited within: 1] [JCR: 10.677]
43.	M. Born, K. Huang Dynamical Theory of Crystal Lattices, Oxford University Press, London (1954) [Cited within: 1]
44.	W. R. L. Lambrecht, B. Segall, M. Methfessel, M. V. Schilfgaarde, Phys. Rev. B, 44 (1991), pp. 3685–3694 [Cited within: 1]
45.	Z. G. Wu, X. J. Chen, V. V. Struzhkin, R. E. Cohen, Phys. Rev. B, 71 (2005), p. 214103 [Cited within: 1]
46.	Z. M. Sun, Y. C. Zhou, Phys. Rev. B, 60 (1999), pp. 1441–1443 [Cited within: 1]
47.	X. Q. Chen, H. Y. Niu, D. Z. Li, Y. Y. Li, Intermetallics, 19 (2011), pp. 1275–1281 [Cited within: 2] [JCR: 1.857]
48.	F. Gao, J. He, E. Wu, S. Liu, D. Yu, D. Li, S. Zhang, Y. Tian, Phys. Rev. Lett. , 91 (2003), p. 015502 [Cited within: 1] [JCR: 7.943]
49.	J. F. Nye Physical Properties of Crystals: Their Representation by Tensors and Matrices, Oxford Science Publications, Oxford (1985) [Cited within: 1]
50.	C. Zener, Phys. Rev. , 71 (1947), pp. 846–851 [Cited within: 1] [JCR: 7.943]
51.	R. P. Ingel, D. Lewis III, J. Am. Ceram. Soc. , 71 (1988), pp. 265–271 [Cited within: 2] [JCR: 2.107]
52.	M. A. Blanco, E. Francisco, V. Luaña, Comput. Phys. Commun. , 158 (2004), pp. 57–72 [Cited within: 1] [JCR: 3.078]
53.	R. Car, M. Parrinello, Phys. Rev. Lett. , 55 (1985), pp. 2471–2474 [Cited within: 1] [JCR: 7.943]
54.	R. D. Shannon, C. T. Prewitt, Acta Crystallogr. B, 25 (1969), pp. 925–946 [Cited within: 1] [JCR: 2.175]
55.	P. Wu, A. D. Pelton, J. Alloy. Compd. , 179 (1992), pp. 259–287 [Cited within: 1] [JCR: 2.39]
56.	B. Liu, J. Y. Wang, Y. C. Zhou, T. Liao, F. Z. Li, Acta Mater. , 55 (2007), pp. 2949–2957 [Cited within: 1] [JCR: 3.941]

2003

0.0

... IntroductionThe efficiency and power of gas-turbine engines used in transportation, energy, and defense sectors rely on the increase of the operated temperature^[1] ...

2005

6.071

0.0

... To increase the operating temperatures of engines, efficient thermal barrier coatings (TBCs) are needed^[2] ...

1998

0.0

... The current material of choice for TBCs is yttria-stabilized zirconia (YSZ) in its metastable tetragonal-prime structure^[3] ...

1981

0.0

... However, the working temperature of YSZ is limited because the metastable tetragonal-prime structure becomes increasingly unstable at high temperature and is apt to decompose to a mixture of tetragonal and cubic zirconia^[4] ...

1998

0.0

... Additionally, the oxygen diffusivity of YSZ is high at high temperature^[5] ...

2005

2.36

0.0

... Y₃Al₅O₁₂, YAG) in particular, are promising candidates for TBCs due to their superior high temperature stability, mechanical and thermal properties^{[6] and [7]} ...

... At high temperature, YAG is stable with Al₂O₃^[6] that is the thermally grown oxide formed on Ni-based superalloys ...

2007

2.36

0.0

Djemia

, F.

Tétard

, K.

Bouamama

, E.

Charron

, D.

Tétard

, Y.

Rabinovitch

, J. Eur. Ceram. Soc. , 27 (2007), pp. 4719–4725

Abstract Brillouin light scattering, Raman light scattering and visible–infrared reflectometry techniques have been used to investigate, respectively, the elastic properties, the phonons and the optical properties of bulk textured polycrystalline yttrium–aluminum garnet doped with 2 at% neodymium obtained by the sintering of commercial oxides. From the analysis of the observed bulk longitudinal and transverse acoustic modes with the knowledge of the refractive index 1.81 inferred from the visible reflectometry, the two independent effective elastic constants of the isotropic polycrystal C 11 = 362 GPa and ( C 11 − C 12 )/2 = 121 GPa are determined leading to the value of the bulk modulus B = ( C 11 + 2 C 12 )/3 = 200 GPa. The ratio ? 0 / ? ∞ = 3.1 and the optic permittivity ? ∞ = 3.46 are derived from the infrared reflectivity data. Pair potential calculations of the three single crystal elastic constants c 11 = 340, c 12 = 127 and c 44 = 112 GPa, of the bulk modulus B = ( c 11 + 2 c 12 )/3 = 198 GPa, of the zone-center (Γ) phonons and of the permittivity function provide good comparison with our experimental results.

... Y₃Al₅O₁₂, YAG) in particular, are promising candidates for TBCs due to their superior high temperature stability, mechanical and thermal properties^{[6] and [7]} ...

1991

0.0

... High-temperature deformation tests on single-crystal YAG showed that YAG is one of the most creep-resistant, non-oxidizing material yet known^{[8] and [9]} ...

1993

0.711

0.0

... High-temperature deformation tests on single-crystal YAG showed that YAG is one of the most creep-resistant, non-oxidizing material yet known^{[8] and [9]} ...

... The isotropy in mechanical behavior of Y₃Al₅O₁₂has been confirmed by previous experimental observation^[9] ...

2012

2.107

0.0

... Recent theoretical results have confirmed the low thermal conductivity of YAG^[10] ...

... The bond lengths and Mulliken population of Yb–O and Al–O bonds of another rare-earth aluminate with the same structure, Y₃Al₅O₁₂, is also included for comparison^[10] ...

... ^[10] theoretically investigated the thermal conductivity of Y₃Al₅O₁₂ ...

2010

2.107

0.0

... ^[11]found that the resistance of YAG to high temperature water corrosion is not quite satisfactory, which is adverse on the integrity and duration of coating ...

... ^[11] reported that Yb₃Al₅O₁₂(YbAG), which shares the same structure with YAG, have superior resistance to vapor corrosion comparing with several other prospective TBC materials, such as Y₃Al₅O₁₂, Y₂Si₂O₇and Yb₂Si₂O₇ ...

... As reported by Klemm^[11], the surface corrosion rate of Yb₃Al₅O₁₂ in hot gas environments is appreciably smaller than those of several other prospective TBC materials, such as Y₃Al₅O₁₂, Y₂Si₂O₇ and Yb₂Si₂O₇ ...

2009

1.789

0.0

, J.

, Y.

Pan

, Q.

Liu

, J.

Guo

, Ceram. Int. , 35 (2009), pp. 25–27

Abstract Nano-sized polycrystalline ytterbium aluminum garnet (YbAG, Yb 3 Al 5 O 12 ) powders were successfully synthesized by a simple urea co-precipitation method. The thermal behavior of the YbAG precursor was investigated. The calcined amorphous YbAG precursor was directly converted to 20–30 nm monophase YbAG at as low as temperature 900 °C, without any other intermediate phases. The nano-sized YbAG powders calcined at 900 °C distributed evenly with a slight aggregation, and the specific surface area of the powders reached 29.7 m 2 g −1 . The absorption spectrum of the YbAG powders was measured, and there were two strong absorption peaks centered at 931 and 965 nm. The results did not correspond to the absorption peaks of Yb:YAG crystal exactly, as the lattice parameters were different between YbAG and YAG.

... Motivated by its potential high temperature applications, several works focused on the preparation of YbAG have been reported recently, by various approaches, such as co-precipitation method ^[12], micro-pulling-down technique ^[13], and RF-heating Czochralski method ^[14] ...

2003

1.846

0.0

2003

1.552

0.0

1.941

0.0

... Then, the theoretical minimum thermal conductivity was estimated from modified Clarke's model^{[15] and [16]}, and the dependence of thermal conductivity of Yb₃Al₅O₁₂on temperature was predicted from Slack's model ^[17] ...

... According to Slack's model^[17] and modified Clarke's model^{[15] and [16]}, the behavior of thermal conductivity at elevated temperatures of a material is accessible ...

... According to the modified Clarke's model^{[15] and [16]}, the theoretical lower limit of intrinsic thermal conductivity (κ_min) can be calculated by: ...

... With the temperature increases further, the thermal conductivity would approach a minimum when the phonon mean-free path decreased to the average atomic distance ^[15] ...

... In addition, as suggested by Clarke ^[15], the strongest influence on the minimum thermal conductivity is the ratio of the atomic weight to the number of atoms per molecule, i ...

... Besides, several additional selection criteria have also been proposed by Clarke^[15] ...

2010

3.941

0.0

Liu

, J. Y.

Wang

, F. Z.

, Y. C.

Zhou

, Acta Mater. , 58 (2010), pp. 4369–4377

Abstract In order to achieve better understanding of the structural/property relationships of La 2 T 2 O 7 ( T = Ge, Ti, Sn, Zr, Hf) pyrochlore, first-principles calculations were conducted to investigate the bonding characteristics, elastic stiffness, structural stability and minimum thermal conductivity. The results show that the relatively weak La–O bonds play a predominant role in determining the structural stability, mechanical and thermal properties of these compounds. In addition, the elastic and thermal properties are influenced when the T atom changes from Ge to Hf. When the bonding strength is enhanced by applying hydrostatic pressure, apart from c 11 , c 12 , and B , which normally increase at high pressures, it is found that the shear elastic moduli, c 44 and G , which relate to the shear deformation resistance, abnormally remain almost constant. The underlying mechanism may help to explain the damage tolerance of pyrochlore compounds. After comprehensive consideration of the elastic anisotropy, a modified David Clarke-type equation is used to calculate the minimum thermal conductivity of the studied pyrochlore materials, which display an extraordinary low thermal conductivity.

... According to Slack's model^[17] and modified Clarke's model^{[15] and [16]}, the behavior of thermal conductivity at elevated temperatures of a material is accessible ...

... According to the modified Clarke's model^{[15] and [16]}, the theoretical lower limit of intrinsic thermal conductivity (κ_min) can be calculated by: ...

... This modified model has been successfully applied to estimate the κ_min of several complex oxides, such as La₂T₂O₇^[16], M P₂O₇^[30], and MPO₄^[31] ...

1973

1.527

0.0

... According to Slack's model^[17] and modified Clarke's model^{[15] and [16]}, the behavior of thermal conductivity at elevated temperatures of a material is accessible ...

... Slack's model describes the intrinsic thermal conductivity of a material over wide range of temperatures, which is expressed as^[17]: ...

... (3))^[17]is a suitable approach to describe the temperature dependence of thermal conductivity when the Umklapp scattering is dominant ...

2002

2.355

0.0

... First-principles calculationsThe first-principles calculations based on the density functional theory (DFT) were performed using the Cambridge Serial Total Energy Package (CASTEP) code ^[18] ...

1993

0.0

... Wherein the Norm-conserving pseudopotentials ^[19] were employed to represent the interactions between the ionic cores and the valence electrons for Yb, Al and O atoms ...

1980

7.943

0.0

... The electronic exchange-correlation energy was treated under the local density approximation (LDA)^[20] ...

2011

3.941

0.0

Feng

, B.

Xiao

, C. L.

Wan

, Z. X.

, Z. C.

Huang

, J. C.

Chen

, R.

Zhou

, W.

Pan

, Acta Mater. , 59 (2011), pp. 1742–1760

Abstract The electronic structure, chemical bonding and mechanical properties of Ln 2 Zr 2 O 7 (Ln = La, Pr, Nd, Sm, Eu and Gd) pyrochlore are investigated by local-density approximation of spin polarized scheme + U calculations ( U is the Hubbard energy) and further verified by the experimental results. Ln 2 Zr 2 O 7 compounds are wide band gap insulators, and this is consistent with the experiment results. The calculated spin polarized density of states of them indicates that they are in a ferromagnetic state and the magnetic moment is mainly attributed to the 4 f shell of the Ln atoms. For the chemical bonds in the Ln 2 Zr 2 O 7 crystals, the O–Zr bond is stronger than the O–Ln bond. The hardness, elastic constants, bulk modulus, shear modulus, Young’s modulus and Poisson’s ratio of Ln 2 Zr 2 O 7 compounds are investigated and the theoretical values are in good agreement with the experiments. The mechanical anisotropic properties are discussed using Zener’s indexes and universal elastic anisotropic index ( A U ). The sound velocities along [1 0 0], [1 1 0] and [1 1 1] directions are calculated for each Ln 2 Zr 2 O 7 crystal. The thermal conductivities of Ln 2 Zr 2 O 7 compounds are evaluated and the obtained thermal conductivity of Ln 2 Zr 2 O 7 is lower than that of yttria-stabilized zirconia, indicating that they could be good low thermally conductive materials at high temperature.

... ^[21] investigated the effects of onsite Coulomb interaction (U correction) on the electronic structures and mechanical properties of Re₂Zr₂O₇ pyrochlore ...

1976

0.0

... The special points sampling integration over Brillouin zone are realized by using the Monkhorst–Pack method with special k-points meshes of 2 × 2 × 2^[22] ...

1997

2.138

0.0

... The free enthalpy, interatomic forces and stresses of the unit cell were minimized under the Broyden–Fletcher–Goldfarb–Shanno (BFGS) minimization scheme ^[23] ...

2001

2.355

0.0

... ^[24] ...

1928

0.0

... The bulk modulus B and shear modulus G were calculated from the compliance tensor based on Voigt–Reuss–Hill approximation^{[25], [26] and [27]} ...

... bulk and shear moduli, Poisson's ratio and Young's modulus, according to Voigt–Reuss–Hill approximation^{[25], [26] and [27]} ...

1929

1.415

0.0

... The bulk modulus B and shear modulus G were calculated from the compliance tensor based on Voigt–Reuss–Hill approximation^{[25], [26] and [27]} ...

... bulk and shear moduli, Poisson's ratio and Young's modulus, according to Voigt–Reuss–Hill approximation^{[25], [26] and [27]} ...

1952

0.0

... The bulk modulus B and shear modulus G were calculated from the compliance tensor based on Voigt–Reuss–Hill approximation^{[25], [26] and [27]} ...

... bulk and shear moduli, Poisson's ratio and Young's modulus, according to Voigt–Reuss–Hill approximation^{[25], [26] and [27]} ...

1993

0.0

... The Young's modulus E_H and Poisson's ratio ν were calculated using Hill's bulk modulus B_Hand shear modulus G_H by the following equations^[28]: ...

2007

0.421

0.0

B. D.

Sand itov

, S. B.

Tsydypov

, D. S.

Sand itov

, Acoust. Phys. , 53 (2007), pp. 594–597

The lattice Grüneisen constant is calculated for amorphous polymers and glasses by using the data on Poisson’s ratio. While the thermodynamic Grüneisen constant of vitreous polymers characterizes the anharmonicity averaged over intrachain and other vibration modes, the lattice Grüneisen constant describes the anharmonicity of interchain vibrations associated with intermolecular interaction. For alkali-silicate glasses, the lattice Grüneisen constant characterizes the anharmonicity of vibrations of the ionic sublattice, which is formed by alkali metal ions and nonbridge oxygen ions.

1.Buryat State University ul. Smolina 24a Ulan-Udé 670000 Russia 2.Russian Academy of Sciences Department of Physical Problems, Buryat Scientific Center, Siberian Division ul. Sakh’yanovo? 6 Ulan-Udé 670047 Russia

... M- is the average mass of the atoms in the crystal, Θ is the Debye temperature, δ³ is the volume per atom, n is the number of atoms in the primitive unit cell, and γ , high temperature limit of the acousticphonon mode Grüneisen parameter, is a direct measure of the anharmonicity of phonon, and can be derived from Poisson's ratio^[29]: ...

2014

2.36

0.0

... This modified model has been successfully applied to estimate the κ_min of several complex oxides, such as La₂T₂O₇^[16], M P₂O₇^[30], and MPO₄^[31] ...

... 43 for spinel)^{[30] and [51]} ...

2013

2.36

0.0

... This modified model has been successfully applied to estimate the κ_min of several complex oxides, such as La₂T₂O₇^[16], M P₂O₇^[30], and MPO₄^[31] ...

1963

1.527

0.0

... The average sound velocity υ_m of a polycrystalline material is defined as ^[32]: ...

... The Debye temperature, Θ_D, was calculated according to the following equation^[32]: ...

1969

7.943

0.0

... Chemical bond theoryDeveloped by Phillips^[33], Van Vechten^[34], Levine ^[35], and Zhang et al ...

1969

7.943

0.0

... Chemical bond theoryDeveloped by Phillips^[33], Van Vechten^[34], Levine ^[35], and Zhang et al ...

1973

1.578

0.0

... Chemical bond theoryDeveloped by Phillips^[33], Van Vechten^[34], Levine ^[35], and Zhang et al ...

... fiμ and fcμ are the ionicity and covalency of A – B bond, and are defined as^[35]: ...

... These two parts of energy can be estimated by^[35]: ...

1996

2.355

0.0

... ^[36], complex chemical bond theory (CBT) provides a simple but efficient approach to study the characteristic of chemical bonds in complex materials, and to predict related physical properties of a crystal from the viewpoint of bonding ...

... The implementation of this theory relies on the decomposition of complex crystal into a linear combination of subformula of various binary crystals^[36] ...

... For a giving chemical formula of a complex crystal, CBT provides an efficient way to decompose it into the following simple subformula^[36]: ...

2003

4.593

0.0

... For every fictitious binary crystal (A_mB_n)^μdecomposed according to CBT, the total lattice energy U^μ can be separated into the ionic part (Uiμ) and the covalent part (Ucμ), which can, respectively, be expressed as^[37]: ...

2007

3.607

0.0

... The lattice energy density u^μ of a binary crystal, which is an essential parameter in estimating the bulk modulus and linear thermal expansion coefficient of a binary crystal, is defined as^[38]: ...

... Then the bulk modulus B^μ of a certain type of binary crystals can be calculated on the basis of lattice energy density^[38]: ...

2007

3.794

0.0

... The bulk modulus of the complex crystals is expressed as^[39]: ...

2006

1.067

0.0

... The linear TEC of a complex crystal is closely related to the lattice energy and can be estimated by the following equations^[40]: ...

... Several approaches have been proposed to estimate TEC theoretically: quasi-harmonic approximation (QHA)^[52], molecular dynamics (MD)^[53], CBT^[40] etc ...

... ^[40] is a simple empirical method to predict the linear expansion coefficients of complex crystals based only on the crystal structure data ...

... They had used this simple method to evaluate the TEC of Y ₃Al₅O₁₂^[40], and the estimated result showed excellent agreement with experimental data ...

... ^[40], the TEC of Yb₃Al₅O₁₂is slightly smaller ...

2004

4.593

0.0

... The calculated lattice parameters of Yb₃Al₅O₁₂ are listed in Table 1, together with previously reported experimental data^[41] for comparison ...

... The bond lengths (l^μ) of all bonds used in the calculation of bond parameters are from the previously reported experimental data ^[41] ...

1929

10.677

0.0

... This can also be testified simply by Pauling's rules^[42]: the strength of a bond equals the ionic valence divided by the coordination number, which yields a strength of 0 ...

1954

0.0

... The mechanical stability of a crystal structure can be justified from the Born–Huang criterion^[43] ...

1991

0.0

... 85^[44], and 0 ...

2005

0.0

... 76 for ZrC^[45], while for a typical ductile ceramic, Ti₃SiC₂, it is 0 ...

1999

0.0

... 65^[46] ...

2011

1.857

0.0

X. Q.

Chen

, H. Y.

Niu

, D. Z.

, Y. Y.

, Intermetallics, 19 (2011), pp. 1275–1281

Abstract Though extensively studied, hardness, defined as the resistance of a material to deformation, still remains a challenging issue for a formal theoretical description due to its inherent mechanical complexity. The widely applied Teter’s empirical correlation between hardness and shear modulus has been considered to be not always valid for a large variety of materials. The main reason is that shear modulus only responses to elastic deformation whereas the hardness links both elastic and permanent plastic properties. We found that the intrinsic correlation between hardness and elasticity of materials correctly predicts Vickers hardness for a wide variety of crystalline materials as well as bulk metallic glasses (BMGs). Our results suggest that, if a material is intrinsically brittle (such as BMGs that fail in the elastic regime), its Vickers hardness linearly correlates with the shear modulus ( H v = 0.151 G ). This correlation also provides a robust theoretical evidence on the famous empirical correlation observed by Teter in 1998. On the other hand, our results demonstrate that the hardness of polycrystalline materials can be correlated with the product of the squared Pugh’s modulus ratio and the shear modulus ( H v=2( k 2 G ) 0.585 −3 where k = G / B is Pugh’s modulus ratio). Our work combines those aspects that were previously argued strongly, and, most importantly, is capable to correctly predict the hardness of all hard compounds known included in several pervious models. Graphical abstract One sentence for highlighted figure: Vickers hardness has been theoretically evidenced to correlate successfully with shear modulus for various bulk metallic glasses (BMGs, left panel) and with a product of the squared Pugh’s modulus ratio and shear modulus for a wide variety of polycrystalline materials (including all superhard materials known, right panel).

... ^[47]proposed an empirical model, which is correlated not only with shear modulus G , but also with bulk modulus B ...

... They found that their model performed well across a large class of materials and hardness values^[47] ...

2003

7.943

0.0

... ^[48]proposed another empirical equation to estimate hardness of covalent crystals: ...

1985

0.0

... The direction-dependence of Young's modulus, E , for Yb₃Al₅O₁₂is given by the following equation^[49]: ...

1947

7.943

0.0

... The isotropy of Young's modulus is also identified by Zener ratio A^[50], which is defined as: A = 2 c₄₄/(c₁₁– c₁₂) ...

1988

2.107

0.0

... [51] ...

... 43 for spinel)^{[30] and [51]} ...

2004

3.078

0.0

... Several approaches have been proposed to estimate TEC theoretically: quasi-harmonic approximation (QHA)^[52], molecular dynamics (MD)^[53], CBT^[40] etc ...

1985

7.943

0.0

... Several approaches have been proposed to estimate TEC theoretically: quasi-harmonic approximation (QHA)^[52], molecular dynamics (MD)^[53], CBT^[40] etc ...

1969

2.175

0.0

... With a same coordination number of 8, the ion radii ^[54] of Y³⁺ (102 pm) is larger than that of Yb³⁺(98 pm) owing to the contraction of the 4f shell ...

1992

2.39

0.0

... For Yb₃Al₅O₁₂, it is stable with alumina till they melt at around 2100 K^[55] ...

2007

3.941

0.0

Liu

, J. Y.

Wang

, Y. C.

Zhou

, T.

Liao

, F. Z.

, Acta Mater. , 55 (2007), pp. 2949–2957

Abstract Elastic stiffness and electronic structure of La 2 Zr 2 O 7 were calculated by means of the first-principles pseudopotential total energy method. The equation of state (EOS), elastic parameters (including the full set of second-order elastic coefficients, bulk modulus and Young’s modulus) and elastic anisotropy were reported. Furthermore, pressure dependence of crystal structure, electronic structure, and bond strengths were investigated. It is found that, although the La 2 Zr 2 O 7 lattice is stable at high pressures, its electronic structure and atomic bonding are definitely disturbed by the applied pressure. The crystal structure of La 2 Zr 2 O 7 approaches that of the fluorite-type lattice at high pressures. The strengths of different interatomic bonds in La 2 Zr 2 O 7 are examined by considering bond-length contractions at various pressures. In addition, the results based on quantum-mechanical-scale calculation clarify the nature of low thermal conductivity of La 2 Zr 2 O 7 at elevated temperatures.

... 31)^[56], the most successful and commercialized thermal barrier material ...